
Det politiske spørgsmål: Skattefradrag for køb af hybridbiler – er det regeringens bedste valg for at reducere brændstofforbruget og kulstofemissionerne?
Beboere i USA og regeringen er bekymrede over afhængigheden af importeret udenlandsk olie og udledningen af kulstof i atmosfæren. I 2005 vedtog kongressen en lov, der giver forbrugerne skattefradrag til køb af el- og hybridbiler.
Dette skattefradrag kan virke som et godt politisk valg, men det er dyrt, fordi det direkte sænker de indtægter, som den amerikanske regering opkræver. Er der mere effektive metoder til at reducere afhængigheden af fossile brændstoffer og kulstofemissioner? Hvordan beslutter vi, hvilken politik der er den bedste? For at besvare dette spørgsmål skal de politiske beslutningstagere forudsige med en vis nøjagtighed, hvordan forbrugerne vil reagere på denne skattepolitik, før disse politiske beslutningstagere bruger millioner af føderale dollars.
Vi kan anvende begrebet nytteværdi på dette politiske spørgsmål. I dette modul vil vi studere nytte og nyttefunktioner. Vi vil derefter kunne bruge en passende nyttefunktion til at udlede indifferencekurver, der beskriver vores politiske spørgsmål.
Udforskning af det politiske spørgsmål
Sæt, at skattefradraget for at subsidiere køb af hybridbiler er en stor succes og fordobler den gennemsnitlige brændstoføkonomi for alle biler på de amerikanske veje – et resultat, der tydeligvis ikke er realistisk, men som er nyttigt for vores efterfølgende diskussioner. Hvad tror du, der ville ske med brændstofforbruget for alle amerikanske bilister? Skal regeringen forvente, at bilernes brændstofforbrug og kulstofemissioner vil falde med halvdelen som reaktion herpå? Hvorfor eller hvorfor ikke?
2.1 Utility Functions
LO 2.1: Beskriv en nyttefunktion.
2.2 Nyttefunktioner og typiske præferencer
LO 2.2: Identificer nyttefunktioner ud fra de typiske præferencer, de repræsenterer.
2.3 Relatering af nyttefunktioner og indifferenskurvekort
LO 2.3: Forklar, hvordan man udleder en indifferenskurve fra en nyttefunktion.
2.4 Find marginalnytte og marginal substitutionsrate
LO 2.4: Udled marginalnytte og MRS for typiske nyttefunktioner.
2.5. Politikspørgsmål
2.1 Nyttefunktioner
LO1: Beskriv en nyttefunktion.
Vores præferencer gør det muligt for os at foretage sammenligninger mellem forskellige forbrugspakker og vælge de foretrukne pakker. Vi kan f.eks. bestemme rangordningen af et helt sæt af bundter på baggrund af vores præferencer. En nyttefunktion er en matematisk funktion, der rangordner bundter af forbrugsgoder ved at tildele et tal til hvert bundt, hvor større tal angiver foretrukne bundter. Utility-funktioner har de egenskaber, som vi identificerede i modul 1 vedrørende præferencer. Det vil sige: de er i stand til at ordne bundter, de er fuldstændige og transitive, mere foretrækkes frem for mindre, og i relevante tilfælde er blandede bundter bedre.
Det tal, som nyttefunktionen tildeler et bestemt bundt, er kendt som nytte, dvs. den tilfredshed, som en forbruger opnår ved et bestemt bundt. Nyttotallet for hvert bundt betyder ikke noget i absolutte tal; der findes ingen ensartet skala, som vi måler tilfredsheden i forhold til. Dens eneste formål er i relative termer: vi kan bruge nytteværdien til at bestemme, hvilke bundter der foretrækkes frem for andre.
Hvis nytteværdien af bundt A er højere end nytteværdien af bundt B, svarer det til at sige, at en forbruger foretrækker bundt A frem for bundt B. Nyttefunktioner rangordner derfor forbrugernes præferencer ved at tildele et tal til hvert bundt. . Vi kan bruge en nyttefunktion til at tegne de indifferenskurvekort, der er beskrevet i modul 1. Da alle bundter på den samme indifferenskurve giver den samme tilfredshed, og ingen af dem derfor er at foretrække, har hvert bundt den samme nytteværdi. Vi kan derfor tegne en indifferenskurve ved at bestemme alle de bundter, der giver det samme tal fra nyttefunktionen.
Økonomer siger, at nyttefunktioner er ordinale snarere end kardinale. Ordinal betyder, at nyttefunktioner kun rangordner bundter – de angiver kun, hvilket bundt der er bedst, ikke hvor meget bedre det er end et andet bundt. Lad os f.eks. antage, at en nyttefunktion angiver, at bundt A giver 10 nytteydelser og bundt B 20 nytteydelser. Vi siger ikke, at bundt B er dobbelt så godt eller 10 utils bedre, men blot at forbrugeren foretrækker bundt B. Antag f.eks. at en veninde deltog i et løb og fortalte dig, at hun kom ind på tredjepladsen. Denne oplysning er ordinal: Du ved, at hun var hurtigere end den fjerdepladsen og langsommere end den andenpladsen. Du kender kun den rækkefølge, i hvilken løberne kom i mål. De enkelte tider er kardinale: Hvis den førstepladsfinalist løb løbet på præcis en time, og din veninde kom i mål på en time og seks minutter, ved du, at din veninde var præcis 10 % langsommere end den hurtigste løber. fordi nyttefunktioner er ordinale, kan mange forskellige nyttefunktioner repræsentere de samme præferencer. Dette er sandt, så længe rækkefølgen er bevaret.
Tag f.eks. nyttefunktionen U, der beskriver præferencer over bundter af varer A og B: U(A,B). Vi kan anvende en hvilken som helst positiv monotonisk transformation på denne funktion (hvilket i bund og grund betyder, at vi ikke ændrer rækkefølgen), og den nye funktion, vi har skabt, vil repræsentere de samme præferencer. Vi kan f.eks. multiplicere en positiv konstant, α , eller tilføje en positiv eller negativ konstant, β . Så αU(A,B)+β repræsenterer nøjagtigt de samme præferencer som U(A,B), fordi den vil ordne bundterne på nøjagtig samme måde. Denne kendsgerning er ganske nyttig, fordi det nogle gange gør det lettere at løse problemer at anvende en positiv monoton transformation af en nyttefunktion.
2.2 Nyttefunktioner og typiske præferencer
LO2: Identificer nyttefunktioner ud fra de typiske præferencer, de repræsenterer
Oplys bundter af æbler, A, og bananer, B. En nyttefunktion, der beskriver Isaks præferencer for bundter af æbler og bananer, er funktionen U(A,B). Men hvad er Isaks særlige præferencer for bundter af æbler og bananer? Lad os antage, at Isak har ret standardpræferencer for æbler og bananer, som fører til vores typiske indifferenskurver: Han foretrækker mere frem for mindre, og han kan lide variation. En nyttefunktion, der repræsenterer disse præferencer, kunne være:
U(A,B) = AB
Hvis æbler og bananer er perfekte komplementer i Isaks præferencer, ville nyttefunktionen se nogenlunde sådan ud:
U(A,B) = MIN,
hvor MIN-funktionen simpelthen tildeler det mindste af de to tal som funktionens værdi.
Hvis æbler og bananer er perfekte substitutter, er nyttefunktionen additiv og ville se nogenlunde sådan ud:
U(A,B) = A + B
En klasse af nyttefunktioner kendt som Cobb-Douglas-nyttefunktioner er meget almindeligt anvendt i økonomi af to grunde:
1. De repræsenterer “velopførte” præferencer, som f.eks. at mere er bedre og præference for variation
2. De er meget fleksible og kan meget let justeres, så de passer til data fra den virkelige verden.
Cobb-Douglas-nyttefunktioner har denne form:
U(A,B) = AαBβ
Da positive monotone transformationer repræsenterer de samme præferencer, kan en sådan transformation bruges til at sætte α + β = 1 , hvilket vi senere vil se er en praktisk betingelse, der forenkler en del matematik i forbrugervalgsproblemet.
En anden måde at transformere nyttefunktionen på en nyttig måde er at tage den naturlige logaritme af funktionen, hvilket skaber en ny funktion, der ser således ud:
U(A,B) = αln(A) + βln(B)
For at udlede denne ligning skal man blot anvende reglerne for naturlige logaritmer. . Det er vigtigt at holde sig abstraktionsniveauet for øje her. Vi kan typisk ikke lave specifikke nyttefunktioner, der præcist beskriver individuelle præferencer. Sandsynligvis er der ingen af os, der kunne beskrive vores egne præferencer med en enkelt ligning. Men så længe forbrugerne generelt har præferencer, der følger vores grundlæggende antagelser, kan vi gøre et ret godt stykke arbejde med at finde nyttefunktioner, der passer til forbrugsdata fra den virkelige verden. Vi vil se beviser på dette senere i kurset.
Tabel 2.1 opsummerer de præferencer og nyttefunktioner, der er beskrevet i dette afsnit.
|
Tabel 2.1 Typer af præferencer og de nyttefunktioner, der repræsenterer dem |
||
|
PREFERENCER |
NYTTEFUNKTIONER FUNKTION |
Type af brugsfunktion |
|
Kærlighed til variation eller “velopdragenhed” |
U(A,B) = AB |
Cobb-Douglas |
|
Love of Variety or “Well Behaved” |
U(A,B) = AαBβ |
Cobb-Douglas |
|
Love of Variety or “Well Behaved” |
U(A,B) = αln(A) + βln(B) |
Naturlig log Cobb-Douglas |
|
Perfekte komplementer |
U(A,B) = MIN |
Min Funktion |
|
Perfekte Substitutter |
U(A,B) = A + B |
Additiv |
2.3 Relatering af nyttefunktioner og indifferenskurvekort
LO3: Forklar, hvordan man udleder en indifferenskurve af en nyttefunktion
Indifferenskurver og nyttefunktioner er direkte relateret til hinanden. Da indifferenskurver repræsenterer præferencer grafisk, og nyttefunktioner repræsenterer præferencer matematisk, følger det faktisk, at indifferenskurver kan udledes af nyttefunktioner.
I univariate funktioner plottes den afhængige variabel på den lodrette akse, og den uafhængige variabel plottes på den vandrette akse, ligesom grafen for y=f(x). I modsætning hertil er graferne for bi-varierede funktioner tredimensionelle, som f.eks. U=U(A,B). Figur 2.1 viser en graf for U=A^\frac{1}{2}}B^\frac{1}{2}. Tredimensionelle grafer er nyttige til at forstå, hvordan nytteværdien stiger med øget forbrug af både A og B.
Figur 2.1 U=A^\frac{1}{2}B^\frac{1}{2}
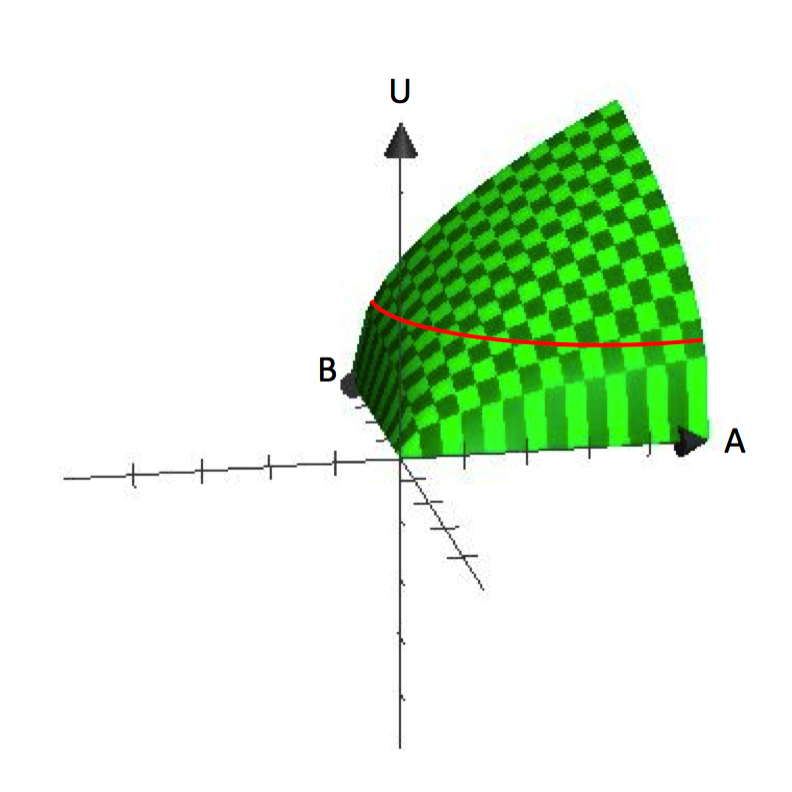
Figur 2.1 viser tydeligt, at det antages, at forbrugerne har en præference for variation. Hvert bundt, som indeholder en bestemt mængde af A og B, repræsenterer et punkt på overfladen. Den lodrette højde på overfladen repræsenterer nytteværdieniveauet. Ved at øge både A og B kan en forbruger nå højere punkter på overfladen.
Så hvor kommer indifferenskurver fra? Husk, at en indifferenskurve er en samling af alle bundter, som en forbruger er ligeglad med, med hensyn til hvilket bundt han eller hun skal forbruge. Matematisk set svarer det til at sige, at alle bundter, når de sættes ind i nyttefunktionen, giver den samme funktionelle værdi. Så hvis vi fastsætter en værdi for nytteværdien, Ū, og finder alle de bundter af A og B, der giver denne værdi, vil vi definere en indifferenskurve. Bemærk, at dette svarer til at finde alle de bundter, der får forbrugeren op i samme højde på den tredimensionelle flade i figur 2.1.
Indifferencekurver er en repræsentation af højde (nytteværdi) på en flad flade. På denne måde svarer de til en konturlinje på et topografisk kort. Ved at føre den tredimensionelle graf tilbage til det todimensionelle rum – A, B-rummet – kan vi vise de konturlinjer/indifferenskurver, der repræsenterer forskellige højder eller brugsniveauer. Af grafen i figur 2.1 kan man allerede se, hvordan denne nyttefunktion giver indifferenskurver, der er “indadbøjede” eller konkave i forhold til oprindelsen.
Så indifferenskurver følger direkte af nyttefunktioner og er en nyttig måde at repræsentere nyttefunktioner på i en todimensionel graf.
2.4 Finde marginalnytte og marginal substitutionsrate
LO4: Udlede marginalnytte og MRS for typiske nyttefunktioner.
Marginalnytte er den ekstra nytte, som en forbruger får ved at forbruge en ekstra enhed af et gode. Matematisk udtrykker vi dette som:
MU_{a}=\frac{\Delta \cup }{\Delta A}
eller ændringen i nytteværdien ved en ændring i mængden af A, der forbruges, hvor Δ repræsenterer en ændring i varens værdi. Så,
MU_{a}=\frac{\Delta \cup }{\Delta A}=\frac{\cup (A+\Delta A,B)-U(A,B)}{\Delta A}
Bemærk, at når vi undersøger den marginale nytte af forbruget af A, holder vi B konstant.
Ved hjælp af beregning er marginalnytten det samme som den partielle afledte af nyttefunktionen med hensyn til A:
MU_{A}\frac{\partiel U(A,B)}{\partiel A}
Tænk på en forbruger, der sætter sig ned for at spise et måltid bestående af salat og pizza. Lad os antage, at vi holder mængden af salat konstant – f.eks. en side salat til en middag. Lad os nu øge antallet af pizzaskiver antage, at med 1skive er nytteværdien 10, med 2 er den 18, med 3 er den 24 og med 4 er den 28. Lad os plotte disse tal på en graf, der har nytteværdien på den lodrette akse og pizza på den vandrette akse (figur 2.2).
Figur 2.2: Graf og tabel over aftagende marginalnytte
|
Pizzaskiver |
Nytte |
Marginalnytte |
Marginalnytten Utility |
|
1 |
10 |
|
|
|
2 |
18 |
8 |
|
|
3 |
24 |
6 |
|
|
4 |
28 |
4 |
|
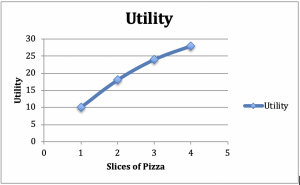
Fra den positive hældning i grafen, kan vi se stigningen i nytteværdien af yderligere pizzaskiver. Ud fra den konkave form på grafen kan vi se et andet almindeligt fænomen: Den ekstra nytte, som forbrugeren får af hvert ekstra pizzasnit, falder med antallet af forbrugte pizzaskiver.
Det faktum, at den ekstra nytte bliver mindre med hvert ekstra pizzasnit, kaldes princippet om aftagende marginalnytte. Dette princip gælder for veludviklede præferencer, hvor blandede bundter er at foretrække.
Marginal substitutionsrate (MRS) er den mængde af en vare, som en forbruger er villig til at give afkald på for at få en enhed mere af en anden vare. Derfor er det det samme som hældningen af indifferencekurven – da vi holder tilfredshedsniveauet konstant, forbliver vi på den samme indifferencekurve, idet vi blot bevæger os langs den, når vi bytter et gode for et andet. Hvor meget af det ene man er villig til at bytte for et mere af det andet, afhænger af den marginale nytte af hvert af dem.
Med udgangspunkt i vores tidligere eksempel, hvis man ved at forbruge en salat mere stiger sin nytte med 10, så kan man ved et nuværende forbrug på 4 pizzaskiver give afkald på 2 pizzaskiver og gå fra 28 til 18 utils. 10 flere utils fra salaten og 10 færre utils ved at opgive 2 pizzaskiver gør, at den samlede nytteværdi er uændret – så vi må stadig befinde os på den samme ligegyldighedskurve. Når man bevæger sig langs indifferenskurven, må man ride på hældningen, dvs. man må opgive varen på den lodrette akse til fordel for mere af varen på den vandrette akse, hvilket giver en negativ stigning over et positivt forløb.
Vi kan gå direkte fra marginalnytte til MRS ved at erkende sammenhængen mellem de to begreber. I vores tilfælde er MRS for en nyttefunktion U=U(A,B) repræsenteret som:
MRS=-\frac{MU_{A}}}{MU_{B}}
Bemærk, at når vi substituerer, kan vi forenkle ligningen:
MRS=-\frac{MU_{A}}{MU_{B}}}=-\frac{\frac{\Delta U}{\Delta A}}}{\frac{\Delta U}{\Delta B}}}=-\frac{\Delta B}}{\Delta A}
Indsætter vi regnearket, svarer det til:
MRS=-\frac{\frac{\frac{\partial U(A,B)}{\partial A}}}{\frac{\partial U(A,B)}{\partial B}}}
2.5 Politisk spørgsmål
Vi fastslog i modul 1, at den relevante forbrugerbeslutning mellem flere kørte kilometer og andet forbrug sandsynligvis er i overensstemmelse med standardantagelserne om forbrugervalg. Derfor er det et godt valg at bruge Cobb-Douglas-nyttefunktionen til at repræsentere en forbruger, som både kan lide at køre bil og forbruge andre varer, og som ser dem som en afvejning (penge brugt på benzin er penge, der ikke bruges på andre forbrugsgoder). Den har også den fordel, at den både er i overensstemmelse med forudsætningerne og er fleksibel:
U(MD,C)=MD^{a}C^{\beta } ,
hvor MD = kørte kilometer og C = Andet forbrug.
Selv funktionen kan faktisk anvendes til virkelige data, hvor parametrene og kan estimeres for dette marked, markedet for kørte kilometer i forbrugerens bil.
Figur 2.3 Graf over indifferenskurver for det politiske eksempel
Udforskning af de politiske spørgsmål:
1 . Ville andre præferencetyper være mere hensigtsmæssige i dette eksempel?
2. Hvad skal være sandt for at perfekte komplementer er den præferencetype, der skal anvendes til at analysere denne politik?
Hvad skal være sandt for perfekte substitutter? I betragtning af, at vi overvejer en “typisk” forbruger, der kører bil, er det da hensigtsmæssigt at vælge en “typisk” nyttefunktion?
4. Er vi bare gætterier, eller har vi et teoretisk grundlag for at støtte vores valg af “velopdragne” præferencer eller en Cobb-Douglas-nyttefunktion?
SAMMENFATNING
Review: Emner og relaterede læringsresultater
2.1 Nyttefunktioner
LO 2.1: Beskrive en nyttefunktion
2.2 Nyttefunktioner og typiske præferencer
LO 2.2: Identificer nyttefunktioner ud fra de typiske præferencer, de repræsenterer
2.3 Relatering af nyttefunktioner og indifferenskurvekort
LO 2.3: Forklar, hvordan man udleder en indifferenskurve fra en nyttefunktion
2.4 Find marginalnytte og marginal substitutionsrate
LO 2.4: Udled marginalnytte og MRS for typiske nyttefunktioner.
2.5. Politisk spørgsmål
Lær: Nøglebegreber og grafer
Bi-variate functions
Cardinal
Konturlinje
Aftagende marginalnytte
Funktion
Marginal substitution rate of substitution (MRS)
Marginalnytte
Ordinal
Univariate funktioner
Util
Utilitet
Nyttefunktion
Grafikker
3D-nyttefunktion og konturlinje
Sammenligninger
Cobb-Douglas
Perfekte komplementer
Perfekte substitutter