I dette projekt vil vi vise, hvordan man bygger en buffer med en transistor. med et par resistorer og kondensatorer.
En buffer er en enhed, der udsender den samme spænding som den, der føres ind i den. den kan tjene et utal af anvendelser, såsom at tillade maksimal spændingsoverførsel og forårsage lav strømbelastning fra en strømforsyning.
Dette kredsløb anvender ikke et integreret kredsløb som en IC-buffer.
Det anvender kun enkle komponenter.
Den transistortype, vi bruger, er en bipolær junctionstransistor af NPN-typen; enhver kan bruges; populære er 2N3904 og 2N2222.
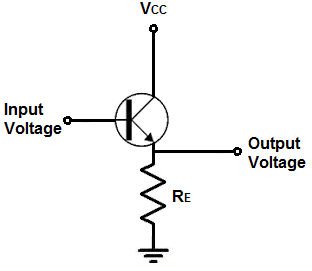
Transistorkredsløbet vil blive konfigureret som en emitterfølger (et andet navn ercommon collector circuit).
Et emitterfølgerkredsløb er et transistorkredsløb, hvor spændingen ved emitteren følger indgangsspændingen. Det er så at sige et spejlbillede af indgangsspændingen. Derfor er spændingen ved udgangen den samme som spændingen ved indgangen.
Da udgangsspændingen er et spejlbillede af indgangsspændingen, og indgangsimpedansen er stor og udgangsimpedansen er lille, fungerer emitterfølgeren som en buffer.
Såfremt en spændingsledning skal være buffer, kan den derfor tilsluttes til indgangen af dette kredsløb, og den belastning, der skal forsynes med strøm, tilsluttes til udgangen af dette kredsløb.
Dette er godt, når man ikke har en bufferchip til rådighed eller en logikchip, som man kan omdanne til en buffer.
I vores kredsløb vil indgangsimpedansen specifikt være over 50KΩ, og udgangsimpedansen vil være ca. 5Ω. Dette er skaber en ret god buffervirkning på enhver spænding, der skal bufferes.
Vi vil konstruere denne type transistorkredsløb til at fungere som buffer.
For at konstruere et emitterfølgerkredsløb korrekt skal der tages hensyn til flere faktorer, herunder hvor meget jævnspænding der tilføres til transistorens kollektor, hvor meget strøm der ønskes ført gennem transistoren og frekvensafskæringen af de vekselstrømssignaler, der kommer ind i indgangen.
Vi vil gennemgå alle disse begreber meget indgående nedenfor. Vi vil i dette kredsløb vise, hvordan det skal konfigureres, og hvordan værdierne af modstande og kondensatorer skal vælges, hvilket kaldes transistorforspænding.
Nødvendige komponenter
- 2N3904 NPN-transistor
- 1KΩ-modstand
- 1.1KΩ-modstand
- 500Ω-modstand
- 16μF elektrolytisk kondensator
- 1600μF elektrolytisk kondensator
Den transistor, der vælges, kan egentlig være en hvilken som helst BJT NPN-transistor. Til dette kredsløb vælger vi transistoren 2N3904.
For mange af værdierne for de komponenter, som vi faktisk beregner, vil du ikke kunne finde de præcise værdier. Nedenfor beregner vi f.eks. en af modstandene til at være 565Ω. Denne modstand findes ikke. Så vi beregner den tilnærmelsesvis. Det er muligt at finde en modstand på 500Ω, og selv hvis du ikke kan finde den, kan du sætte 2 1KΩ-modstande parallelt for at få en tilsvarende modstand på 500Ω.
En 1,1KΩ-modstand vil du heller ikke finde. Så du kan enten tilnærme den ned til 1KΩ eller sætte en 1KΩ-modstand i serie med en 100Ω-modstand. Til alle grundlæggende formål er dette ikke nødvendigt. Du kan blot tilslutte en 1KΩ-modstand i stedet for 1,1KΩ. Det giver lignende resultater.
De samme tilnærmelser skal bruges til kondensatorværdierne. Find en værdi, der ligger så tæt på de beregnede kondensatorværdier som muligt, og brug dem.
Transistorbufferkredsløb
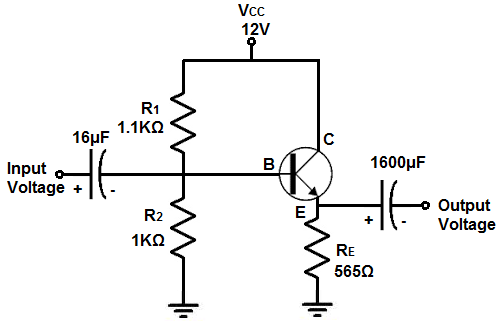
Det bufferkredsløb, vi skal bygge med en enkelt NPN BJT-transistorog et par modstande og kondensatorer, er vist nedenfor.
Brødpladekredsløbet af ovenstående kredsløb er vist nedenfor. 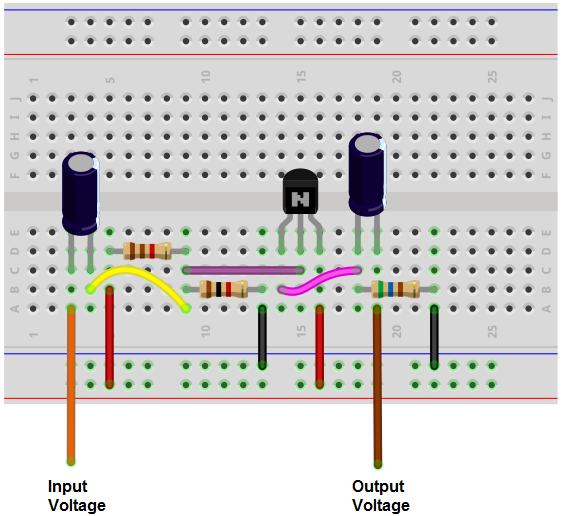
Sådan fungerer ovenstående kredsløb som en buffer. Den linje, der skal bufferes, bliver tilsluttet til indgangen, og den belastning, der skal tændes, bliver tilsluttet til kredsløbets udgang.
Vi vil nu komme ind på detaljerne om, hvorfor de forskellige komponenter er nødvendige for kredsløbet, og hvordan man vælger værdierne for dem.
Så den første ting er, at vi beslutter, hvor meget spænding vi vil tilføre dette kredsløb. Det er den spænding, VCC, der tilføres til transistorens kollektor. Du kan virkelig vælge en hvilken som helst værdi fra over VB, basisspændingen, til den maksimale værdi, som transistoren kan håndtere på kollektoren. Dette er typisk 40-60 V på de fleste transistorer. For vores kredsløb vil vi vælge en fornuftig spændingsværdi på 12 for VCC, så dette er den første overvejelse.
Næst, nu hvor vi kender VCC, biaser vi kredsløbets basisspænding, hvilket vi betyder, at vi vælger den spænding, som vi ønsker skal falde over transistorens base. hvilken værdi ønsker vi over basen? For at besvare dette ser vi på det samlede billede. Den vekselspændingsmængde, der kan være til stede ved transistorens udgang, afhænger af det jævnspændingsområde, som kredsløbet har. I den ene ende af spektret kan transistoren svinge op til 12V, hvilket er VCC. I den anden ende af spektret kan transistoren svinge ned til næsten jord, ca. 0,7 V. Grunden til, at transistoren ikke kan svinge helt til jord, er, at transistoren ikke vil tænde, medmindre dioden er tændt, og det sker ved ca. 0,7V, som er barrierespændingen for den interne diode. Derfor er 0,7V kredsløbets bund og ikke jord eller 0V. Med en strømforsyning på 12V og en jord 0,7V kan transistoren derfor svinge fra 0,7V og op til 12V. Hvorfor dette har betydning for den spænding, som vi leverer til basen, er, at uanset hvilken spænding der kommer ind i kredsløbet, har den en bund på 0,7 V og et loft på 12 V. Derfor ønsker vi at biasere basisspændingen, så den falder mellem disse værdier. Dette giver et maksimalt peak-to-peak-udslag for signalet og giver det mest plads til at fungere uden at klippe. Hvis basisspændingen er biased forkert eller langt fra midten, kan transistoren få betydelig clipping, der giver dårligt output. For et loft på 12 V og et gulv på 0,7 V vil middelværdien være (12 – 0,7 V)/2 +0,7 V = 6,35 V. Vi er nødt til at tage diode-spændingsfaldet i betragtning, fordi værdien ved basen er 0,7V højere end ved udgangen. Ved at biase basisspændingen lige i midten af loftet og gulvet giver det mulighed for maksimal svingning af vekselstrømssignalet, kaldet maksimal peak-to-peak-ekskursion. Når man biaser et transistorkredsløb, der beskæftiger sig med vekselstrømssignaler, svarer det vekselstrømssignal, der vil kunne forekomme ved udgangen uden at blive klippet, tilDC-biasering. AC-signalet vil kun kunne svinge så langt som DC-spændingsforspændingen tillader det. Hvis strømforsyningen er 20 V og gulvet er 0,7 V, kan transistoren svinge fra en spidsværdi på 20 V til et gulv på 0,7 V. Ved at placere transistoren i midtpunktet af disse spændinger kan vekselstrømssignalet svinge maksimalt fra loftet til gulvet. Dette er det optimale DC-driftspunkt for kredsløbet, kaldet Q-punktet eller hvilepunktet.Hvis du vælger en DC-værdi for lav, vil du få signalet til at klippe tidligere i bunden af bølgeformen. Hvis du vælger en DC-driftsspænding for høj, vil du få signalet til at klippe i toppen af bølgeformen.
Så på baggrund af dette punkt ønsker vi, at spændingen ved basen skal være midtvejs mellem 12V, forsyningsspændingen, og 0,7V, som repræsenterer gulvet. Så at VB= 0,7V + (12V-0,7V)/2, hvilket er 6,35V. Så for at få denne spænding er vi nødt til at vælge vores modstande, der gør det muligt at få denne spænding til at forekomme ved basen. Spændingen ved basen er spændt gennem 2 modstande. Modstandene danner en spændingsdeler og deler forsyningsspændingen. Vi kan dele vores forsyningsspænding til en hvilken som helst spænding, der er mindre end strømforsyningen, ved at vælge den korrekte værdi af modstande. Basisspændingen, VB= VCC * (R2/R1+R2). For at løse denne ligning vælger vi værdien af den ene modstand og beregner derefter værdien af den anden modstand på grundlag af denne modstandsværdi ud fra denne formel. Så for R2-modstanden vælges en værdi på 1KΩ som referencepunkt for den anden modstand. Når vi sætter disse værdier ind i formlen, får viVB= VCC * (R2/R1+R2)= 6,35V (12V) (1KΩ). /(R1+1KΩ). Når vi regner, giver det en værdi på R1= 1,1KΩ. Så for at få en værdi på 6,35V ved basen er værdierne af modstandene R1 lig med 1,1KΩ og R2=1KΩ.
Næst skal vi bestemme værdien af RE-modstanden. Den værdi, vi vælger, er integreret, så vi ikke overophedes og muligvis ødelægger transistoren. Hvordan vi vælger RE er baseret på værdien af den strøm, IE, som vi ønsker følgende gennem transistoren, og hvad der er en sikker strøm til at flyde gennem transistoren. Så vi vælger bare et interval, som er en sikker strøm, der kan løbe gennem transistoren, uden at den brænder sammen. En sikker strøm er 10 mA. Det er en anstændig mængde strøm og en, der ikke vil brænde transistoren ud. Så emittermodstanden, RE= VE/IE, hvor VE er spændingen over emitteren og IE er den strøm, der løber gennem emitteren. VE=VB-0,7V = 5,65V. Den eneste spændingsforskel mellem basisspændingen og emitterspændingen er diode-spændingsfaldet mellem de to forbindelsespunkter. Da transistoren har en diode i sig fra basen til emitteren, har transistoren et internt spændingsfald. Derfor er emitterspændingen lig med basisspændingen minus spændingsfaldet over dioden. Så formlen, RE= VE/IE= 5,65V/10mA= 565Ω. Så en RE-modstand på ca. 500Ω ville være tilstrækkeligt godt til dette kredsløb.
Nu skal vi til sidst vælge værdien af kondensatorerne i dette kredsløb. Begge kondensatorer har den samme funktion. De lader kun vekselstrømssignalet passere og blokerer for, at jævnstrømmen passerer. De fungerer således som koblingskondensatorer.
Vi vil først vise, hvordan vi beregner værdien af kondensatoren ved indgangen.
For at vælge en passende kondensatorværdi korrekt skal vi tage hensyn til mange ting, som vi nu vil gennemgå.
For det første skal vi bestemme kredsløbets cutoff-frekvens. Dette er den frekvens, som vi ønsker filtreret fra. Hvis man har med lydsignaler at gøre, er det frekvensområde, der er hørbart for mennesker, 20 Hz til 20.000 Hz. Hvis du bygger vores transistor, så vi kun vil have hørbare signaler igennem, er 20 Hz en god afskæringsfrekvens at vælge. Det betyder, at enhver frekvens i dette område eller lavere vil blive filtreret ud til jord. Så vi vil vælge 20Hz som vores cutoff-frekvens. Hvis vi tager 20Hz og anvender det på vinkelfrekvensen ω=2πf, får vi ω=2πf≈125s-1. Dette er den ene del af ligningen.
Den næste ting vi skal overveje er værdien af den modstand, som kondensatoren ser. Den første del af dette kredsløb fra kondensatoren og den modstand, som den ser, ned til jord, danner et højpasfilter, et RC-højpasfilter. Et RC-højpasfilter er et kredsløb, der består af en kondensator med en modstand forbundet til jord.
Hvis du visualiserede strømmen, der flyder ind i kredsløbet, kan strømmen gå enten 1 af 3 veje. Strømmen kan gå gennem kondensatoren og gennem R2-modstanden og ned til jord. Strømmen kan gå gennem kondensatoren og gennem R1-modstanden. Eller strømmen kan løbe gennem transistoren og løbe gennem RE-modstanden ned til jord. Det kan virke mærkeligt, at strømmen kan løbe gennem R1-modstanden, men vekselstrømssignaler ser også jævnspændingsniveauer som jord. Så selv om den er på DC-niveauet 12V (gennem R1), kan den for vekselstrømssignaler også være jord; det er derfor, at den også kan være en vej ned til jord.
Så det er de 3 måder, hvorpå strømmen kan løbe i kredsløbet. EVen selvom strømmen kan tage disse veje, er det i sidste endehvad en kondensator ser, der bestemmer den reelle modstand, som den støder på. Så vi vil tale om dette nu. Modstanderne R1og R2 er parallelle. Derfor ser kondensatoren den ækvivalente modstand af disse 2 parallelle modstande. Kondensatoren ser altså 1KΩ parallelt med 1,1KΩ-modstanden. Den ækvivalente modstand for disse modstande er ca. 500Ω. Så dette er den modstand, som kondensatoren ser på én vej. Den anden vej er, når strømmen går gennem transistoren og gennem modstanden RE. Denne modstand vil være βRE. Med β lig med ca. 100, og ved at lave denne matematik, beregnes denne modstand til56KΩ.
Husk, at strømmen altid tager den vej med mindst mulig modstand. Så mellem mulighederne 500Ω eller 56KΩ vil strømmen naturligvis tage 500Ω-vejen.
Så 500Ω er den ækvivalente modstand, som RC-højpasfilternetværket ser, og vi ved, at vi ønsker en afskæringsfrekvens på 20 Hz. Og beregning af vinkelfrekvensen for 20Hz giver os, ω=2πf≈125s-1.
Så går vi til ligningen, REQC1= 1/125s-1= (500Ω)C1= 0,008s. Når man regner det ud, giver det en C1-værdi på 16µF. Så den første kondensator er 16µF.
Nu går vi videre til den anden kondensator. Og den er valgt på samme måde som den første kondensator.
Vi ønsker, at den anden kondensator skal reagere på samme måde som den første kondensator med hensyn til den frekvens, vi har med at gøre. Det skyldes, at det samme frekvenssignal, der er input, er output. Så man ønsker at matche frekvensresponsen for begge kondensatorer. Så for udgangskondensatoren beregner vi også den i henhold til dens frekvensrespons på 20 Hz. Ved at beregne vinkelfrekvensen får vi igen, ω=2πf≈125s-1.
Vi bruger igen den samme formel, REQC2= 1/125s-1.
Hvad er REQ i dette tilfælde? REQ er den modstand, som udgangskondensatoren ser i kredsløbet. Hvis vi ser fra kondensatoren tilbage til indgangssiden, ser kondensatoren en modstand på (R1 || R2)/β= (1,1KΩ || 1KΩ)/100= (523Ω/100) ≈ 5Ω. Udgangskondensatoren ser altså en ækvivalent modstand på 5Ω, når den ser tilbage til kredsløbets indgang.
Så hvis man sætter disse værdier ind i ligningen, får man REQC2= 1/125s-1= (5Ω)C2= 0,008s. Når vi løser C2, får vi 1600µF. Dette er altså værdien af udgangskondensatoren.
Og nu har vi løst alle værdierne for komponenterne i kredsløbet.
Du kan se på baggrund af beregningerne, at kredsløbet har en høj indgangsimpedans og en lav udgangsimpedans. Som vi beregnede, er indgangsimpedansen βRE, som vi beregnede til at være 56KΩ. Udgangsimpedansen beregnede vi til at være 5Ω. Så du kan se, hvordan dette kredsløb har en høj indgangsimpedans og en lav udgangsimpedans.
Så det fungerer meget godt som en buffer.
Dette kredsløb kan tilføjes til en spændingsledning, der skal bufferes, hvilket gør det muligt at overføre al spænding, samtidig med at det giver en udgang med lav impedans, så en belastning kan forsynes.
Viden om, at dette er et grundlæggende bufferkredsløb. Det er ikke så nøjagtigt som en egentlig bufferchip. For det første har en bufferchip en større impedans og en lavere udgangsimpedans. For det andet er det ikke et helt nøjagtigt spændingsfølgerkredsløb. Da transistoren har en intern diode, der har et spændingsfald, der nogenlunde svarer til 0.7V, mister den denne spænding ved udgangen. Så udgangssignalet er 0,7 V lavere end indgangssignalet. Så du kan se, at det ikke helt er en spændingsfølger.
Men til alle grundlæggende formål fungerer den dog meget godt som en buffer med lav præcision.