Standardafvigelsen er den gennemsnitlige variabilitet i dit datasæt. Den fortæller dig, hvor langt hver værdi i gennemsnit ligger fra gennemsnittet.
En høj standardafvigelse betyder, at værdierne generelt ligger langt fra gennemsnittet, mens en lav standardafvigelse indikerer, at værdierne er samlet tæt på gennemsnittet.
Hvad fortæller standardafvigelse dig?
Standardafvigelse er et nyttigt mål for spredning for normalfordelinger.
I normalfordelinger er data symmetrisk fordelt uden skævhed. De fleste værdier samler sig omkring et centralt område, og værdierne aftager i takt med, at de bevæger sig længere væk fra centrum. Standardafvigelsen fortæller dig, hvor spredt dine data i gennemsnit er fra midten af fordelingen.
Mange videnskabelige variabler følger normalfordelinger, herunder højde, standardiserede testresultater eller vurderinger af jobtilfredshed. Når du har standardafvigelserne for forskellige stikprøver, kan du sammenligne deres fordelinger ved hjælp af statistiske test for at drage konklusioner om de større populationer, de kommer fra.
Middelværdien (M) er den samme for hver gruppe – det er den værdi på x-aksen, når kurven er på sit højeste punkt. Men deres standardafvigelser (SD) adskiller sig fra hinanden.
Standardafvigelsen afspejler spredningen i fordelingen. Kurven med den laveste standardafvigelse har en høj top og en lille spredning, mens kurven med den højeste standardafvigelse er mere flad og spredt.
Den empiriske regel
Standardafvigelsen og middelværdien kan tilsammen fortælle dig, hvor de fleste af værdierne i din fordeling ligger, hvis de følger en normalfordeling.
Den empiriske regel, eller 68-95-99,7-reglen, fortæller dig, hvor dine værdier ligger:
- Omkring 68% af scorerne ligger inden for 2 standardafvigelser fra middelværdien,
- Omkring 95% af scorerne ligger inden for 4 standardafvigelser fra middelværdien,
- Omkring 99.7% af pointtallene ligger inden for 6 standardafvigelser fra gennemsnittet.
Som følge af den empiriske regel:
- Omkring 68% af scorerne ligger mellem 40 og 60.
- Omkring 95% af scorerne ligger mellem 30 og 70.
- Omkring 99,7 % af pointtallene ligger mellem 20 og 80.
Den empiriske regel er en hurtig måde at få et overblik over dine data på og kontrollere, om der er outliers eller ekstreme værdier, der ikke følger dette mønster.
For ikke-normale fordelinger er standardafvigelsen et mindre pålideligt mål for variabilitet og bør anvendes i kombination med andre mål som f.eks. intervallet eller interkvartilområdet.
Standardafvigelsesformler for populationer og stikprøver
Der anvendes forskellige formler til beregning af standardafvigelser, afhængigt af om du har data fra en hel population eller en stikprøve.
Populationsstandardafvigelse
Når du har indsamlet data fra alle medlemmer af den population, som du er interesseret i, kan du få en nøjagtig værdi for populationsstandardafvigelsen.
Formlen for populationens standardafvigelse ser således ud:
| Formel | Forklaring |
|---|---|
 |
|
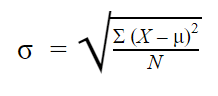Stikprøvens standardafvigelse
Når man indsamler data fra en stikprøve, bruges stikprøvens standardafvigelse til at foretage skøn eller slutninger om populationens standardafvigelse.
Stikprøvens standardafvigelsesformel ser således ud:
| Formel | Forklaring |
|---|---|
 |
|
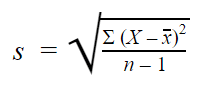Med stikprøver bruger vi n – 1 i formlen, fordi brugen af n ville give os et skævt skøn, som konsekvent undervurderer variabiliteten. Stikprøvens standardafvigelse ville have en tendens til at være lavere end den reelle standardafvigelse for populationen.
Reducerer man stikprøven n til n – 1, bliver standardafvigelsen kunstigt stor, hvilket giver et konservativt skøn over variabiliteten.
Selv om dette ikke er et uvildigt skøn, er det et mindre skævt skøn over standardafvigelsen: Det er bedre at overvurdere end at undervurdere variabiliteten i stikprøver.
Strin til beregning af standardafvigelsen
Standardafvigelsen beregnes normalt automatisk af den software, du bruger til din statistiske analyse. Men du kan også beregne den i hånden for bedre at forstå, hvordan formlen fungerer.
Der er seks hovedtrin til at finde standardafvigelsen i hånden. Vi vil bruge et lille datasæt med 6 scoringer til at gennemgå trinene.
| Datasæt | |||||
|---|---|---|---|---|---|
| 46 | 69 | 32 | 60 | 52 | 41 |
Trin 1: Find gennemsnittet
For at finde gennemsnittet skal du lægge alle pointtallene sammen og derefter dividere dem med antallet af pointtal.
x̅ = (46 + 69 + 32 + 60 + 52 + 41) ÷ 6 = 50
Trin 2: Find hver scores afvigelse fra middelværdien
Subtraher middelværdien fra hver score for at få afvigelserne fra middelværdien.
Da x̅ = 50, trækker vi her 50 fra hver score.
| Score | Afvigelse fra middelværdien |
|---|---|
| 46 | 46 – 50 = -4 |
| 69 | 69 – 50 = 19 |
| 32 | 32 – 50 = -18 |
| 60 | 60 – 50 = 10 |
| 52 | 52 – 50 = 2 |
| 41 | 41 – 50 = -9 |
Trin 3: Kvadratér hver afvigelse fra middelværdien
Multiplicer hver afvigelse fra middelværdien med sig selv. Dette vil resultere i positive tal.
(-4)2 = 4 × 4 = 16
192 = 19 × 19 = 361
(-18)2 = -18 × -18 = 324
102 = 10 × 10 = 100
22 = 2 × 2 = 4
(-9)2 = -9 × -9 = 81
Trin 4: Find summen af kvadrater
Tilpas alle de kvadrerede afvigelser. Dette kaldes summen af kvadrater.
16 + 361 + 324 + 100 + 4 + 81 = 886
Trin 5: Find variansen
Divider summen af kvadrater med n – 1 (for en stikprøve) eller N (for en population) – dette er variansen.
Da vi arbejder med en stikprøve på 6, bruger vi n – 1, hvor n = 6.
886 ÷ (6 – 1) = 886 ÷ 5 = 177.2
Trin 6: Find kvadratroden af variansen
For at finde standardafvigelsen tager vi kvadratroden af variansen.
√177,2 = 13,31
Fra at lære at SD = 13.31, kan vi sige, at hver score afviger fra gennemsnittet med 13,31 point i gennemsnit.
Hvorfor er standardafvigelse et nyttigt mål for variabilitet?
Og selv om der findes enklere måder at beregne variabilitet på, vægter formlen for standardafvigelse ujævnt spredte prøver mere end jævnt spredte prøver. En højere standardafvigelse fortæller dig, at fordelingen ikke blot er mere spredt, men også mere ujævnt spredt.
Det betyder, at den giver dig et bedre billede af dine datas variabilitet end enklere mål, såsom den gennemsnitlige absolutte afvigelse (MAD).
Den gennemsnitlige absolutte afvigelse (MAD) ligner standardafvigelsen, men er lettere at beregne. Først udtrykker du hver afvigelse fra gennemsnittet i absolutte værdier ved at omdanne dem til positive tal (f.eks. bliver -3 til 3). Derefter beregner du gennemsnittet af disse absolutte afvigelser.
I modsætning til standardafvigelsen behøver du ikke at beregne kvadrater eller kvadratrødder af tal for MAD. Men af den grund giver den dig et mindre præcist mål for variabilitet.
Lad os tage to stikprøver med samme centrale tendens, men med forskellige mængder variabilitet. Prøve B er mere variabel end prøve A.
| Værdier | Middelværdi | Middelværdi absolut afvigelse | Standardafvigelse | |
|---|---|---|---|---|
| Stikprøve A | 66, 30, 40, 64 | 50 | 15 | 17.8 |
| Stikprøve B | 51, 21, 79, 49 | 50 | 15 | 23,7 |
For stikprøver med samme gennemsnitlige afvigelser fra middelværdien kan MAD ikke skelne mellem spredningsniveauer. Standardafvigelsen er mere præcis: den er højere for stikprøven med større variabilitet i afvigelserne fra gennemsnittet.
Gennem kvadrering af forskellene fra gennemsnittet afspejler standardafvigelsen ujævn spredning mere nøjagtigt. Dette trin vægter ekstreme afvigelser tungere end små afvigelser.
Dette gør imidlertid også standardafvigelsen følsom over for outliers.
Hyppigt stillede spørgsmål om standardafvigelse
Variabilitet måles oftest med følgende beskrivende statistikker:
- Rækkevidde: forskellen mellem den højeste og laveste værdi
- Interkvartilområde: intervallet i den midterste halvdel af en fordeling
- Standardafvigelse: gennemsnitlig afstand fra middelværdien
- Varians: gennemsnit af kvadrerede afstande fra middelværdien
Standardafvigelsen er det gennemsnitlige omfang af variabilitet i dit datasæt. Den fortæller dig, hvor langt hver enkelt værdi i gennemsnit ligger fra gennemsnittet.
I normalfordelinger betyder en høj standardafvigelse, at værdierne generelt ligger langt fra gennemsnittet, mens en lav standardafvigelse indikerer, at værdierne er samlet tæt på gennemsnittet.
I en normalfordeling er data symmetrisk fordelt uden skævhed. De fleste værdier samler sig omkring et centralt område, og værdierne aftager i takt med, at de bevæger sig længere væk fra centrum.
Målene for central tendens (middelværdi, modus og median) er nøjagtig de samme i en normalfordeling.
Den empiriske regel, eller 68-95-99,7-reglen, fortæller dig, hvor de fleste værdier ligger i en normalfordeling:
- Omkring 68 % af værdierne ligger inden for 1 standardafvigelse fra middelværdien.
- Omkring 95 % af værdierne ligger inden for 2 standardafvigelser fra middelværdien.
- Omkring 99.7 % af værdierne ligger inden for 3 standardafvigelser fra gennemsnittet.
Den empiriske regel er en hurtig måde at få et overblik over dine data på og kontrollere, om der er outliers eller ekstreme værdier, der ikke følger dette mønster.
Varians er de gennemsnitlige kvadrerede afvigelser fra middelværdien, mens standardafvigelse er kvadratroden af dette tal. Begge mål afspejler variabiliteten i en fordeling, men deres enheder er forskellige:
- Standardafvigelse udtrykkes i de samme enheder som de oprindelige værdier (f.eks. minutter eller meter).
- Varians udtrykkes i meget større enheder (f.eks. meter i kvadrat).
Og selv om enhederne for varians er sværere at forstå intuitivt, er varians vigtig i statistiske test.