I denne lektion vil vi vise en nem strategi til at løse følgende opgave: hvordan man finder arealet af en ligebenet trekant.
Lad os sætte en række af de egenskaber, som vi hidtil har bevist, i praksis i følgende geometriopgave:
Problem
I en ligebenet trekant, ΔABC, med benlængde 10, er højden til basen lig med to tredjedele af basen. Find arealet af trekanten.
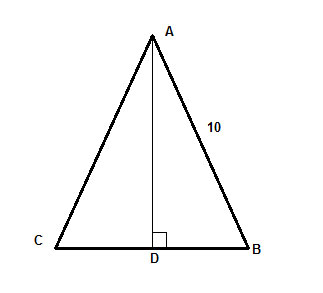
Strategi
For at løse denne opgave arbejder vi baglæns ud fra, hvad vi skal gøre.
Vi skal finde arealet af trekanten, som vi ved er givet ved formlen (basis gange højde)/2.
Et problem vi har er, at vi ikke kender hverken basislængden eller højden. Men vi har fået oplyst forholdet mellem dem, hvilket er et hint om, hvad vi skal gøre. Lad os kalde basislængden, BC, x.
Derpå ved vi, at højden, AD, er 2x/3, som angivet i opgaven.
Så det svar, vi leder efter, er (basis gange højde)/2, eller x gange 2x/3, divideret med to.
Men hvordan finder vi x? Der er yderligere to ting, vi fik i opgaven, som vi ikke har brugt endnu – benets længde (10) og det faktum, at der er tale om en ligebenet trekant. Vi skal sandsynligvis bruge disse to ting for at løse opgaven.
Lad os gennemgå egenskaberne ved ligebenede trekanter. En ting, der straks bør springe i øjnene, er, at som vi har vist, at i en ligebenet trekant er højden til basen halvdeler basen, så CD=DB=x/2.
Endeligt er AD højden, hvilket betyder, at vinklen ∠ADC er en ret vinkel, og vi har en retvinklet trekant, ΔADC, hvis hypotenuse vi kender (10) og kan bruge til at finde benene ved hjælp af Pythagoras sætning, c2 =a2+b2,
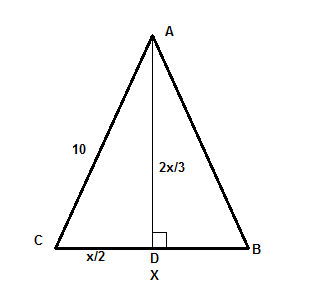
hvor c= 10 ,a=x/2 og b=2x/3 . Og vi er færdige, resten er bare algebraisk løsning for x.
Bevis: Arealet af en ligebenet trekant
(1) ΔADC er en retvinklet trekant //givet, da AD er højden til basen
(2) AC2 =CD2 + AD2 //Pythagoræiske sætning
(3) AC= 10 //givet
(4) CB = x
(5) CD = x/2 //Højden til basen i ligebenet trekant halverer basen
(6) AD = 2x/3 //givet
(7) 102 = (x/2)2 + (2x/3)2 //Substituere i (2)
(8) 100 = x2/4+4×2/9 //simplificere
(9) 100*36 = 9×2 +16×2 //multiplicere begge sider med 36
(10) 100*36 = 25×2 //samle lignende udtryk