I den moderne tidsalder inden for lyd kan du ikke undgå at høre om “Hi-Res” og 24-bit “Studio Quality”-musik. Hvis du ikke har spottet tendensen i high-end smartphones – Sonys LDAC Bluetooth-codec – og streamingtjenester som Tidal, så skal du virkelig begynde at læse mere på dette websted.
Løftet er enkelt – overlegen lyttekvalitet takket være flere data, også kaldet bit-dybde. Det er 24 bit af digitale enere og nuller i modsætning til de sølle 16 bit fra cd-æraen. Selvfølgelig skal du betale ekstra for disse produkter og tjenester af højere kvalitet, men flere bits er da helt sikkert bedre, ikke sandt?
“Low res”-lyd vises ofte som en trappeformet bølgeform. Det er ikke sådan, hvordan audio sampling fungerer, og det er ikke sådan, lyden ser ud, når den kommer ud af en enhed.
Nikke nødvendigvis. Behovet for højere og højere bitdybder er ikke baseret på den videnskabelige virkelighed, men snarere på en fordrejning af sandheden og udnyttelse af forbrugernes manglende kendskab til videnskaben om lyd. I sidste ende har firmaer, der markedsfører 24-bit lyd, langt mere at vinde i profit end du har i overlegen afspilningskvalitet.
Bit-dybde og lydkvalitet: Trappetrin er ikke noget
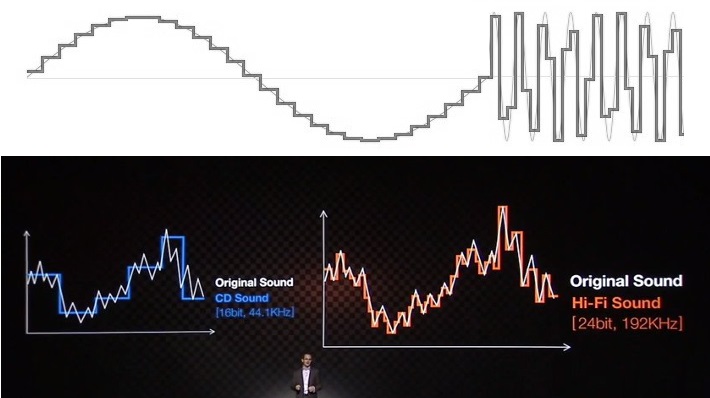
For at antyde, at 24-bit lyd er et must-have, tropper virksomhederne (og alt for mange andre, der forsøger at forklare dette emne) op med den meget velkendte lydkvalitetstrappe til himlen. 16-bit eksemplet viser altid en ujævn, takkede gengivelse af en sinusbølge eller et andet signal, mens 24-bit tilsvarende ser smukt glat og med højere opløsning ud. Det er et simpelt visuelt hjælpemiddel, men et, der bygger på uvidenhed om emnet og videnskaben for at føre forbrugerne til de forkerte konklusioner.
Hvor nogen nu bider mig i hovedet, så er det teknisk set sådan, at disse trappetrinseksempler i nogen grad giver et korrekt billede af lyd i det digitale domæne. Et stamplot/lollipop-diagram er imidlertid en mere præcis grafisk fremstilling af visuel lydprøvetagning end disse trappetrin. Tænk på det på denne måde – en prøve indeholder en amplitude på et meget specifikt tidspunkt, ikke en amplitude, der holdes i en specifik tidsperiode.

Brugen af trappediagrammer er bevidst vildledende, når stamdiagrammer giver en mere præcis gengivelse af digital lyd. Disse to grafer viser de samme datapunkter, men trappediagrammet virker meget mindre nøjagtigt.
Det er imidlertid korrekt, at en analog til digital konverter (ADC) skal passe et uendeligt analogt lydsignal ind i et endeligt antal bits. En bit, der falder mellem to niveauer, skal afrundes til den nærmeste tilnærmelse, hvilket er kendt som en kvantiseringsfejl eller kvantiseringsstøj. (Husk dette, for vi vender tilbage til det.)
Hvis man ser på lydudgangen fra enhver digital til analog lydkonverter (DAC), der er bygget i dette århundrede (og sandsynligvis længe før det), vil man imidlertid ikke kunne se nogen trappetrin. Ikke engang hvis man udsender et 8-bit signal. Så hvad sker der?

En 8-bit, 10kHz sinusbølgeudgang optaget fra en billig Pixel 3a-smartphone. Vi kan se noget støj, men ingen mærkbare trappetrin, som så ofte skildres af lydfirmaer.
Først og fremmest er det, som disse trappetrinsdiagrammer beskriver, hvis vi anvender dem på en lydudgang, noget, der kaldes en nul-ordens-hold DAC. Dette er en meget enkel og billig DAC-teknologi, hvor et signal skifter mellem forskellige niveauer for hver ny prøve for at give et output. Dette bruges ikke i nogen professionelle eller halvdårlige forbrugerlydprodukter. Du kan måske finde den i en mikrocontroller til 5 dollars, men bestemt ikke andre steder. En forkert fremstilling af lydudgange på denne måde indebærer en forvrænget, upræcis bølgeform, men det er ikke det, du får.

I virkeligheden er en moderne ∆Σ DAC-udgang et oversamplet 1-bit PDM-signal (til højre), snarere end et nul-hold-signal (til venstre). Sidstnævnte giver et analogt output med mindre støj, når det filtreres.
Audio-grade ADC’er og DAC’er er overvejende baseret på delta-sigma (∆Σ)-modulation. Komponenter af denne kaliber omfatter interpolation og oversampling, støjformning og filtrering for at udjævne og reducere støj. Delta-sigma DAC’er konverterer lydprøver til en 1-bit strøm (pulse-density modulation) med en meget høj samplingfrekvens. Når det filtreres, giver det et glat udgangssignal med støj, der er skubbet langt ud af de hørbare frekvenser.
Kort sagt: Moderne DAC’er udsender ikke ru udseende takkede lydprøver – de udsender en bitstrøm, der er støjfiltreret til et meget præcist, glat output. Denne trappetrinsvisualisering er forkert på grund af noget, der kaldes “kvantiseringsstøj.”
Forståelse af kvantiseringsstøj
I ethvert endeligt system sker der afrundingsfejl. Det er rigtigt, at en 24-bit ADC eller DAC vil have en mindre afrundingsfejl end en tilsvarende 16-bit, men hvad betyder det egentlig? Og endnu vigtigere, hvad hører vi egentlig? Er det forvrængning eller fuzz, er detaljerne tabt for evigt?
Det er faktisk lidt af begge dele, afhængigt af om man befinder sig i det digitale eller analoge område. Men nøglebegrebet for at forstå begge dele er at få styr på støjgulvet, og hvordan dette forbedres, når bitdybden øges. For at demonstrere det skal vi træde tilbage fra 16 og 24 bit og se på eksempler med meget lille bitdybde.
Forskellen mellem 16 og 24 bitdybder er ikke nøjagtigheden i formen af en bølgeform, men den tilgængelige grænse, før digital støj forstyrrer vores signal.
Der er en hel del ting at tjekke i eksemplet nedenfor, så først en kort forklaring på, hvad vi kigger på. Vi har vores input (blå) og kvantiserede (orange) bølgeformer i de øverste diagrammer, med bitdybder på 2, 4 og 8 bit. Vi har også tilføjet en lille mængde støj til vores signal for bedre at simulere den virkelige verden. Nederst har vi en graf over kvantiseringsfejlen eller afrundingsstøjen, som beregnes ved at trække det kvantiserede signal fra indgangssignalet.

Kvantiseringsstøjen stiger, jo mindre bitdybden er, på grund af afrundingsfejl.
Den øgede bitdybde gør helt klart, at det kvantiserede signal passer bedre til indgangssignalet. Det er dog ikke det, der er vigtigt, se det meget større fejl/støjsignal for de lavere bitdybder. Det kvantiserede signal har ikke fjernet data fra vores input, det har faktisk tilføjet i dette fejlsignal. Additiv syntese fortæller os, at et signal kan reproduceres ved summen af to andre signaler, herunder signaler i ude af fase, der fungerer som subtraktion. Det er sådan, støjudligning fungerer. Så disse afrundingsfejl introducerer et nyt støjsignal.
Det er ikke kun teoretisk, man kan faktisk høre mere og mere støj i lydfiler med lavere bitdybde. For at forstå hvorfor, skal du undersøge, hvad der sker i 2-bit-eksemplet med meget små signaler, f.eks. før 0,2 sekunder. Klik her for at se en indzoomet grafik. Meget små ændringer i indgangssignalet giver store ændringer i den kvantiserede version. Dette er afrundingsfejlen i aktion, som har den virkning, at den forstærker støj fra små signaler. Så endnu en gang bliver støjen højere, når bitdybden falder.
Kvantisering fjerner ikke data fra vores input, den tilføjer faktisk et støjende fejlsignal.
Tænk også omvendt: Det er ikke muligt at opfange et signal, der er mindre end størrelsen af kvantiseringstrinnet – ironisk nok kendt som den mindst betydende bit. Små signalændringer skal hoppe op til det nærmeste kvantiseringsniveau. Større bitdybder har mindre kvantiseringstrin og dermed mindre niveauer af støjforstærkning.
Det vigtigste er dog at bemærke, at kvantiseringsstøjens amplitude forbliver konstant, uanset amplituden af indgangssignalerne. Dette viser, at støjen forekommer på alle de forskellige kvantiseringsniveauer, så der er et ensartet støjniveau for enhver given bitdybde. Større bitdybder giver mindre støj. Vi bør derfor tænke på forskellene mellem 16 og 24 bit-dybder ikke som nøjagtigheden i en bølgeforms form, men som den tilgængelige grænse, før digital støj forstyrrer vores signal.
Bit-dybde handler om støj
Nu, hvor vi taler om bit-dybde i forhold til støj, skal vi vende tilbage til vores ovenstående grafik en sidste gang. Bemærk, hvordan 8-bit eksemplet ligner et næsten perfekt match for vores støjende indgangssignal. Det skyldes, at dets 8-bit opløsning faktisk er tilstrækkelig til at indfange niveauet af baggrundsstøjen. Med andre ord: kvantiseringstrinets størrelse er mindre end støjens amplitude, eller signal/støjforholdet (SNR) er bedre end baggrundsstøjniveauet.
Ligningen 20log(2n), hvor n er bitdybden, giver os SNR. Et 8-bit signal har et SNR på 48dB, 12-bits er 72dB, mens 16-bit rammer 96dB, og 24-bits hele 144dB. Dette er vigtigt, fordi vi nu ved, at vi kun har brug for en bitdybde med tilstrækkelig SNR til at rumme det dynamiske område mellem vores baggrundsstøj og det højeste signal, vi ønsker at optage, for at gengive lyd så perfekt, som den forekommer i den virkelige verden. Det bliver lidt tricky at bevæge sig fra de relative skalaer i den digitale verden til de lydtryksbaserede skalaer i den fysiske verden, så vi vil forsøge at holde det enkelt.
Vi har brug for en bitdybde med tilstrækkelig SNR til at rumme vores baggrundsstøj for at optage vores lyd så perfekt, som den lyder i den virkelige verden.
Dit øre har en følsomhed, der spænder fra 0dB (stilhed) til ca. 120dB (smertefuldt høj lyd), og den typiske evne til at skelne lydstyrker er kun 1dB fra hinanden. Så dit øres dynamikområde er ca. 120 dB eller tæt på 20 bit.
Du kan dog ikke høre alt dette på én gang, da trommehinden eller trommehinden strammer sig for at reducere den mængde lydstyrke, der rent faktisk når frem til det indre øre i høje omgivelser. Du skal heller ikke lytte til musik i nærheden af så højt, for så bliver du døv. Desuden er de miljøer, som du og jeg lytter til musik i, ikke så stille, som sunde ører kan høre. Et velbehandlet lydstudie kan bringe os ned under 20 dB for baggrundsstøj, men at lytte i en travl stue eller i bussen vil naturligvis forværre forholdene og mindske vores behov for et højt dynamisk område.
Det menneskelige øre har et enormt dynamisk område, men bare ikke alt på én gang. Maskering og høreværn reducerer dets effektivitet.
Oven i det hele: Efterhånden som lydstyrken stiger, virker maskering af højere frekvenser i øret. Ved lave lydstyrker på 20 til 40 dB forekommer maskering ikke, undtagen for lyde tæt på hinanden i tonehøjde. Men ved 80 dB vil lyde under 40 dB blive maskeret, mens lyde under 70 dB ved 100 dB er umulige at høre. Ørets og lyttematerialets dynamiske karakter gør det svært at give et præcist tal, men det reelle dynamiske område for din hørelse ligger sandsynligvis i nærheden af 70 dB i et gennemsnitligt miljø og ned til kun 40 dB i meget høje miljøer. En bitdybde på blot 12 bit ville sandsynligvis dække de fleste mennesker, så 16-bit-cd’er giver os masser af plads.

hyperfysik Der opstår højfrekvent maskering ved høje lyttevolumener, hvilket begrænser vores opfattelse af mere stille lyde.
De fleste instrumenter og optagemikrofoner introducerer også støj (især guitarforstærkere), selv i meget stille optagestudier. Der er også foretaget et par undersøgelser af dynamikområdet for forskellige genrer, herunder denne, som viser et typisk dynamikområde på 60 dB. Det er ikke overraskende, at genrer med en større forkærlighed for stille dele, såsom kor, opera og klaver, viste maksimale dynamiske intervaller omkring 70 dB, mens “højere” rock-, pop- og rapgenrer havde en tendens til 60 dB og derunder. I sidste ende produceres og optages musik kun med en vis nøjagtighed.
Du er måske også bekendt med musikindustriens “loudness wars”, som helt sikkert modarbejder formålet med nutidens Hi-Res-lydformater. Kraftig brug af komprimering (som forstærker støj og dæmper spidser) reducerer det dynamiske område. Moderne musik har betydeligt mindre dynamisk rækkevidde end plader fra 30 år siden. Teoretisk set kunne moderne musik distribueres med lavere bit-hastigheder end gammel musik. Du kan se det dynamiske område for en række mange albums her.

CD-kvalitet er måske “kun” 16 bit, men det er overkill for kvaliteten.
16 bit er alt, hvad du behøver
Dette har været noget af en rejse, men forhåbentlig er du kommet med et langt mere nuanceret billede af bitdybde, støj og dynamisk område end de misvisende trappeeksempler, du så ofte ser.
Bit-dybde handler om støj, og jo flere bits data du har til at lagre lyd: jo mindre kvantiseringsstøj vil der blive indført i din optagelse. På samme måde vil du også være i stand til at optage mindre signaler mere nøjagtigt, hvilket hjælper med at drive det digitale støjgulv ned under optagelses- eller lyttemiljøet. Det er alt det, vi har brug for bit-dybde til at gøre. Der er ingen fordel ved at bruge store bitdybder til lydmastere.
Overraskende nok er 12 bit nok til en anstændigt klingende musikmaster og til at imødekomme det dynamiske område i de fleste lyttemiljøer. Digital lyd transporterer imidlertid mere end blot musik, og eksempler som tale eller miljøoptagelser til tv kan gøre brug af et større dynamisk område end det meste musik gør. Desuden har lidt headroom til adskillelse mellem højt og lavt aldrig skadet nogen.
I alt taget i betragtning giver 16 bit (96 dB dynamisk område eller 120 dB med dithering) plads til en bred vifte af lydtyper samt grænserne for den menneskelige hørelse og typiske lyttemiljøer. De perceptuelle stigninger i 24-bit-kvaliteten er yderst diskutable, hvis de ikke blot er placebo, som jeg håber, at jeg har vist. Desuden gør stigningen i filstørrelser og båndbredde dem unødvendige. Den komprimeringstype, der anvendes til at skrumpe filstørrelsen af dit musikbibliotek eller stream, har en langt mere mærkbar indvirkning på lydkvaliteten, end om det er en 16- eller 24-bit fil.