MesopotamiskRediger
Perioden 2700-2300 f.Kr. var den første forekomst af den sumeriske abakus, en tabel med på hinanden følgende kolonner, som afgrænsede de successive størrelsesordener i deres sexagesimale talsystem.
Nogle forskere peger på et tegn i babylonisk kileskrift, som kan være afledt af en gengivelse af abakussen. Det er oldbabyloniske lærde som Carruccio, der mener, at oldbabylonierne “kan have brugt abacus til operationer som addition og subtraktion; dette primitive apparat viste sig dog at være vanskeligt at bruge til mere komplekse beregninger”.
EgyptianEdit
Brug af abakus i det gamle Egypten nævnes af den græske historiker Herodot, som skriver, at egypterne manipulerede stenene fra højre til venstre, modsat i retning af den græske metode fra venstre til højre. Arkæologer har fundet antikke skiver i forskellige størrelser, som menes at have været brugt som tællere. Der er dog ikke blevet fundet væggen af afbildninger af dette instrument.
PersiskRediger
Under Akameniderne begyndte perserne omkring 600 f.Kr. for første gang at bruge abakus. Under de parthiske, sassanidiske og iranske imperier koncentrerede de lærde sig om at udveksle viden og opfindelser med landene omkring dem – Indien, Kina og Romerriget, hvor man mener, at den blev eksporteret til andre lande.
GreekEdit
De tidligste arkæologiske beviser for brugen af den græske abakus stammer fra det 5. århundrede f.Kr. Også Demosthenes (384 f.Kr.-322 f.Kr.) talte om, at man skulle bruge sten til beregninger, der var for vanskelige for hovedet. I et skuespil af Alexis fra det 4. århundrede f.Kr. nævnes en abakus og småsten til regnskaber, og både Diogenes og Polybius nævner mænd, der nogle gange stod for mere og andre gange for mindre, ligesom småstenene på en abakus. Den græske abakus var et bord af træ eller marmor, der var forudindstillet med små tællere i træ eller metal til matematiske beregninger. Denne græske abakus blev brugt i det akæmænidiske Persien, i den etruskiske civilisation, i det gamle Rom og indtil den franske revolution i den vestlige kristne verden.
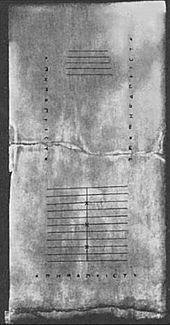
En tavle, der blev fundet på den græske ø Salamis i 1846 e.Kr. (Salamistavlen), stammer fra 300 f.Kr. og er dermed den ældste tælletavle, der hidtil er blevet fundet. Det er en plade af hvidt marmor 149 cm lang, 75 cm bred og 4,5 cm tyk, hvorpå der er 5 grupper af markeringer. I midten af tavlen er der et sæt af 5 parallelle linjer, der er ligeligt delt af en lodret linje, og som krones af en halvcirkel ved skæringspunktet mellem den nederste vandrette linje og den eneste lodrette linje. Under disse linjer er der et bredt felt med en vandret revne, der deler det. Under denne revne er der en anden gruppe på 11 parallelle linjer, der igen er delt i to dele af en linje vinkelret på dem, men med halvcirklen øverst i skæringspunktet; den tredje, sjette og niende af disse linjer er markeret med et kryds ved deres skæringspunkt med den lodrette linje. Fra denne periode stammer også Darius-vasen, som blev udgravet i 1851. Den var dækket af billeder, herunder en “kasserer”, der holder en vokstavle i den ene hånd, mens han med den anden hånd manipulerer tællere på et bord.
KinesiskEdit

| Abacus | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Traditionel kinesisk | 算盤 | |||||||||||||||
| Simplificeret kinesisk | 算盘 | |||||||||||||||
| Litterær betydning | “beregningsbakke” | |||||||||||||||
| Transskriptioner | Standardmandarin | Hanyu Pinyin | IPA | Yue: Kantonesisk | Yale Romanization | Jyutping | IPA | Southern Min | Hokkien POJ | Tâi-lô | ||||||
Den tidligste kendte skriftlige dokumentation af den kinesiske abakus stammer fra det 2. århundrede f.Kr.
Den kinesiske abakus, kendt som suanpan (算盤/算盘, lit. “regnebakke”), er typisk 20 cm høj og findes i forskellige bredder afhængig af operatøren. Den har normalt mere end syv stænger. Der er to perler på hver stang i det øverste dæk og fem perler hver i det nederste. Perlerne er normalt afrundede og lavet af et hårdt træ. Perlerne tælles ved at flytte dem op eller ned mod bjælken; perler, der flyttes mod bjælken, tælles, mens perler, der flyttes væk fra den, ikke tælles. En af de øverste perler er 5, mens en af de nederste perler er 1. Hver stang har et tal under sig, der viser stedværdien.Suanpanen kan straks nulstilles til udgangspositionen ved en hurtig bevægelse langs den vandrette akse for at dreje alle perlerne væk fra den vandrette bjælke i midten.
Prototypen på den kinesiske abakus opstod under Han-dynastiet, og perlerne er ovale. Song-dynastiet og tidligere brugte den 1:4 type eller fire perler abakus, der ligner den moderne abakus, herunder formen på perlerne, der almindeligvis er kendt som abakus i japansk stil.
I det tidlige Ming-dynasti begyndte abakussen at dukke op i form af 1:5 abakus. Det øverste dæk havde én perle og det nederste havde fem perler.
I slutningen af Ming-dynastiet optrådte abakusstilerne i form af 2:5. Det øverste dæk havde to perler, og det nederste havde fem perler.
Der blev udtænkt forskellige beregningsteknikker til Suanpan, der muliggjorde effektive beregninger. Der findes i dag skoler, der lærer eleverne at bruge det.
I den lange skriftrulle Langs floden under Qingming-festivalen, malet af Zhang Zeduan under Song-dynastiet (960-1297), er en suanpan tydeligt synlig ved siden af en regnskabsbog og lægens recepter på disken i en apotekerværksted (Feibao).
Ligheden mellem den romerske abacus og den kinesiske antyder, at den ene kunne have inspireret den anden, da der er visse beviser for et handelsforhold mellem Romerriget og Kina. Der kan dog ikke påvises nogen direkte forbindelse, og ligheden mellem abakuserne kan være tilfældig, idet begge i sidste ende stammer fra tælling med fem fingre pr. hånd. Hvor den romerske model (ligesom de fleste moderne koreanske og japanske) har 4 plus 1 perle pr. decimalplads, har standard suanpan 5 plus 2. Dette giver i øvrigt mulighed for at anvende et hexadecimalt talsystem (eller en hvilken som helst base op til 18), som kan have været anvendt til traditionelle kinesiske vægtangivelser. (I stedet for at løbe på ledninger som i de kinesiske, koreanske og japanske modeller løber perlerne i den romerske model i riller, hvilket formentlig gør aritmetiske beregninger meget langsommere.
En anden mulig kilde til suanpanen er kinesiske tællestænger, som opererede med et decimalsystem, men som manglede begrebet nul som pladsholder. Nulpunktet blev sandsynligvis indført hos kineserne i Tang-dynastiet (618-907), da rejser i Det Indiske Ocean og Mellemøsten ville have givet direkte kontakt med Indien, hvilket gjorde det muligt for dem at erhverve begrebet nul og decimalpunktet fra indiske købmænd og matematikere.
RomanEdit

Den normale beregningsmetode i det gamle Rom var, ligesom i Grækenland, ved at flytte tællere på et glat bord. Oprindeligt blev der brugt småsten (calculi). Senere, og i middelalderens Europa, blev der fremstillet jetoner. Markerede linjer angav enheder, femmere, tiere osv. som i det romerske talsystem. Dette system med “tællere” fortsatte i det sene romerske imperium og i middelalderens Europa og blev fortsat brugt i begrænset omfang indtil det nittende århundrede. På grund af pave Sylvester II’s genindførelse af abakussen med ændringer blev den igen udbredt i Europa i løbet af det 11. århundrede Denne abakus anvendte perler på ledninger i modsætning til de traditionelle romerske tælletavler, hvilket betød, at abakussen kunne bruges meget hurtigere.
Horace, der skrev i det 1. århundrede f.Kr., henviser til voksabakussen, et bræt dækket af et tyndt lag sort voks, hvorpå søjler og tal blev indskrevet ved hjælp af en stylus.
Et eksempel på arkæologiske beviser på den romerske abakus, som her er vist i en rekonstruktion, stammer fra det 1. århundrede e.Kr. Den har otte lange riller med op til fem perler i hver og otte kortere riller med enten én eller ingen perler i hver. Rillen markeret med I angiver enheder, X tiendedele, og så videre op til millioner. Perlerne i de kortere riller angiver fem – fem enheder, fem tiendedele osv., i det væsentlige i et bi-kvinært kodet decimalsystem, der er beslægtet med de romerske tal. De korte riller til højre kan have været brugt til at markere romerske “ounces” (dvs. brøker).
IndianEdit
The Abhidharmakośabhāṣya af Vasubandhu (316-396), et sanskrit-værk om buddhistisk filosofi, fortæller, at filosoffen Vasumitra fra det andet århundrede e.Kr. sagde, at “at placere en væge (sanskrit vartikā) på tallet et (ekāṅka) betyder, at det er et et, mens det at placere vægen på tallet hundrede betyder, at det kaldes et hundrede, og på tallet tusind betyder, at det er et tusind”. Det er uklart præcis, hvad dette arrangement kan have været. Allerede omkring det 5. århundrede fandt indiske kontorister nye måder at registrere indholdet af Abacus’en på. Hinduistiske tekster brugte udtrykket śūnya (nul) til at betegne den tomme kolonne på abakussen.
JapanskRediger

På japansk kaldes abakussen soroban (算盤, そろばん, lit. “Tællebakke”), som blev importeret fra Kina i det 14. århundrede. Den var sandsynligvis i brug af arbejderklassen et århundrede eller mere, før den herskende klasse begyndte, da klassestrukturen ikke tillod, at apparater, der blev brugt af underklassen, blev overtaget eller brugt af den herskende klasse. 1/4-abakussen, som fjerner den sjældent anvendte anden og femte perle, blev populær i 1940’erne.
Den japanske abakus i dag er af typen 1:4. Abakussen med fire perler blev indført fra Kina i Muromachi-æraen. Den antager formen med det øverste dæk én perle og de nederste fire perler. Den øverste perle på det øverste dæk var lig med fem og den nederste er lig med en ligesom den kinesiske eller koreanske abakus, og decimaltallet kan udtrykkes, så abakussen er udformet som en fire abakus. Perlerne er altid i form af en diamant. Kvotesdivisionen anvendes generelt i stedet for divisionsmetoden; samtidig anvendes divisionsmultiplikationen for at gøre multiplikations- og divisionscifrene konsekvent for at gøre divisionsmultiplikationen. Senere havde Japan en 3:5 abakus kaldet 天三算盤, som nu er Ize Rongji-samlingen i Shansi Village i Yamagata City. Der var også 2:5 type abakus.
Med udbredelsen af fireperle abakus er det også almindeligt at bruge japanske abakus rundt om i verden. Der findes også forbedrede japanske abakus forskellige steder. En af de japansk fremstillede abakus fremstillet i Kina er en abakus med aluminiumsramme af plastikperler. Filen er ved siden af de fire perler, og “clearing”-knappen, tryk på clearing-knappen, sæt straks den øverste perle til den øverste position, den nederste perle er drejet til den nederste position, straks clearing, let at bruge.
Abacus er stadig fremstillet i Japan i dag, selv med udbredelsen, praktiske og overkommelige lomme elektroniske lommeregneres udbredelse og prisvenlighed. Der undervises stadig i brugen af soroban i japanske grundskoler som en del af matematikken, primært som et hjælpemiddel til hurtigere mental beregning. Ved hjælp af det visuelle billede af en soroban kan man nå frem til svaret på samme tid som, eller endda hurtigere end det er muligt med et fysisk instrument.
KoreanEdit
Den kinesiske abacus migrerede fra Kina til Korea omkring 1400 e.Kr. Koreanerne kalder den jupan (주판), supan (수판) eller jusan (주산).Den fire perler abacus( 1:4 ) blev indført til Korea Goryeo Dynasty fra Kina under Song Dynasty, senere blev den fem perler abacus (5:1) abacus indført til Korea fra Kina under Ming Dynasty.
Native AmericanEdit


Nogle kilder nævner brugen af en abakus kaldet en nepohualtzintzin i den gamle aztekiske kultur. Denne mesoamerikanske abakus brugte et 5-cifret base-20-system. ordet Nepōhualtzintzin kommer fra nahuatl og er dannet af rødderne; Ne – personlig -; pōhual eller pōhualli – kontoen -; og tzintzin – små lignende elementer. Dens fulde betydning blev opfattet som: at en person tæller med små lignende elementer. Dens brug blev lært i Calmecac til temalpouhqueh , som var studerende, der var dedikeret til at tage regnskaber for himlen, fra barndommen.
Nepōhualtzintzin var opdelt i to hoveddele adskilt af en bar eller en mellemliggende snor. I den venstre del var der fire perler, som i den første række har ensartede værdier (1, 2, 3 og 4), og i højre side er der tre perler med værdier på henholdsvis 5, 10 og 15. For at kende værdien af de respektive perler i de øverste rækker er det nok at gange med 20 (ved hver række), værdien af den tilsvarende konto i den første række.
I alt var der 13 rækker med 7 perler i hver række, hvilket udgjorde 91 perler i hver Nepōhualtzintzin. Dette var et grundlæggende tal til at forstå, 7 gange 13, en tæt relation, der blev opfattet mellem naturfænomener, underverdenen og himlens cyklusser. En Nepōhualtzintzin (91) repræsenterede antallet af dage, som en årstid varer, to Nepōhualtzintzin (182) er antallet af dage i majsens cyklus, fra såning til høst, tre Nepōhualtzintzin (273) er antallet af dage i en babys drægtighed, og fire Nepōhualtzintzin (364) fuldendte en cyklus og svarer omtrent til et år (11/4 dage for lidt). Oversat til moderne computeraritmetik svarede Nepōhualtzintzin til rang fra 10 til 18 i floating point, som beregnede stjernestørrelser såvel som infinitesimale beløb med absolut præcision, hvilket betød, at ingen afrunding var tilladt.
Den fornyede opdagelse af Nepōhualtzintzin skyldtes den mexicanske ingeniør David Esparza Hidalgo, der på sine vandringer i Mexico fandt diverse graveringer og malerier af dette instrument og rekonstruerede flere af dem udført i guld, jade, indkapslinger af skaller osv. Der er også blevet fundet meget gamle Nepōhualtzintzin, der tilskrives Olmec-kulturen, og endda nogle armbånd af mayaoprindelse, samt en mangfoldighed af former og materialer i andre kulturer.
George I. Sanchez, “Arithmetic in Maya”, Austin-Texas, 1961 fandt en anden base 5, base 4 abacus på Yucatán-halvøen, som også beregnede kalenderdata. Dette var en fingerabacus, på den ene hånd blev der brugt 0, 1, 2, 3 og 4; og på den anden hånd blev der brugt 0, 1, 2 og 3. Bemærk brugen af nul i begyndelsen og slutningen af de to cyklusser. Sanchez arbejdede sammen med Sylvanus Morley, en kendt mayaforsker.
Inkaernes quipu var et system af farvede knyttede snore, der blev brugt til at registrere numeriske data, ligesom avancerede tally sticks – men ikke brugt til at udføre beregninger. Beregninger blev udført ved hjælp af en yupana (Quechua for “tælleværktøj”; se figur), som stadig var i brug efter erobringen af Peru. Funktionsprincippet for en yupana er ukendt, men den italienske matematiker Nicolino De Pasquale fremsatte i 2001 et forslag til en forklaring på det matematiske grundlag for disse instrumenter. Ved at sammenligne formen på flere yupanas fandt forskerne ud af, at beregningerne var baseret på Fibonacci-sekvensen 1, 1, 1, 2, 3, 5 og potenser af 10, 20 og 40 som stedværdier for de forskellige felter i instrumentet. Ved at bruge Fibonacci-sekvensen kunne man holde antallet af korn i et enkelt felt på et minimum.
RussianEdit

Den russiske abakus, schoty (russisk: счёты, plural fra russisk: счёт, tælling), har normalt et enkelt skråt dæk med ti perler på hver tråd (undtagen en tråd, som normalt er placeret tæt på brugeren, med fire perler til kvartrubelbrøker). Ældre modeller har endnu en tråd med fire perler til kvart-kopeks, som blev præget indtil 1916. Den russiske abakus bruges ofte lodret, med hver tråd fra venstre mod højre som linjer i en bog. Trådene er normalt bøjet, så de buler opad i midten for at holde perlerne fastgjort til en af de to sider. Den ryddes, når alle perler flyttes til højre. Under manipulationen flyttes perlerne til venstre. For at gøre det lettere at se, er de 2 midterste perler på hver tråd (den 5. og 6. perle) normalt af en anden farve end de andre otte perler. Ligeledes kan den venstre perle på tusindtråden (og milliontråden, hvis den er til stede) have en anden farve.
Som et simpelt, billigt og pålideligt apparat var den russiske abakus i brug i alle butikker og markeder i hele det tidligere Sovjetunionen, og der blev undervist i brugen af den i de fleste skoler indtil 1990’erne. Selv opfindelsen i 1874 af den mekaniske regnemaskine, Odhner-aritmometeret, havde ikke erstattet dem i Rusland; ifølge Yakov Perelman var det kendt, at nogle forretningsmænd, der forsøgte at importere sådanne apparater til det russiske imperium, selv i hans tid opgav og forlod landet i fortvivlelse efter at have fået vist en dygtig abakusoperatørs arbejde. Ligeledes har masseproduktionen af Felix-aritmometre siden 1924 ikke reduceret brugen af dem væsentligt i Sovjetunionen. Den russiske abakus begyndte først at miste sin popularitet, efter at masseproduktionen af mikroberegnerne var begyndt i Sovjetunionen i 1974. I dag betragtes den som en arkaisme og er erstattet af den håndholdte lommeregner.
Den russiske abakus blev bragt til Frankrig omkring 1820 af matematikeren Jean-Victor Poncelet, der tjente i Napoleons hær og havde været krigsfange i Rusland. Abakussen var gået ud af brug i Vesteuropa i det 16. århundrede med fremkomsten af decimalnotationen og algoritmiske metoder. For Poncelets franske samtidige var den noget nyt. Poncelet brugte den ikke til noget anvendt formål, men som et undervisnings- og demonstrationsredskab. Tyrkerne og armenierne brugte også abakusser, der lignede den russiske schoty. Den blev kaldt coulba af tyrkerne og choreb af armenierne.