A Concise Introduction to Logic

9.1 Et historisk eksempel

Filosoffen David Hume (1711-1776) er kendt for at være en strålende skeptisk empiriker. En person er skeptiker i forhold til et emne, hvis denne person både har meget strenge standarder for, hvad der udgør viden om dette emne, og også mener, at vi ikke kan leve op til disse strenge standarder. Empirisme er det synspunkt, at vi primært opnår viden gennem erfaring, især gennem oplevelser med vores sanser. I sin bog An Inquiry Concerning Human Understanding opstiller Hume sine principper for viden og råder os derefter til at rydde op i vores biblioteker:

Når vi løber over biblioteker, overbeviste om disse principper, hvilken ødelæggelse skal vi så lave? Hvis vi f.eks. tager et bind om guddommelighed eller skolemetafysik i hånden, lad os da spørge: Indeholder det nogen abstrakte ræsonnementer om mængde eller antal? Nej. Indeholder det nogen eksperimentelle ræsonnementer om faktiske forhold og eksistens? Nej. Overlad det så til flammerne, for det kan ikke indeholde andet end sofisteri og illusion.

Hume mente, at de eneste kilder til viden var logiske eller matematiske ræsonnementer (som han ovenfor kalder “abstrakte ræsonnementer vedrørende kvantitet eller antal”) eller sanseerfaring (“eksperimentelle ræsonnementer vedrørende fakta og eksistens”). Hume er foranlediget til at hævde, at enhver påstand, der ikke er baseret på den ene eller den anden metode, er værdiløs.

Vi kan rekonstruere Humes argumentation på følgende måde. Antag, at t er et eller andet emne, som vi hævder at have viden om. Antag, at vi ikke har fået denne viden gennem erfaring eller logik. Skrevet på engelsk kan vi rekonstruere hans argument på følgende måde:

Vi har viden om t, hvis og kun hvis vores påstande om t er lært af eksperimentelle ræsonnementer eller af logik eller matematik.

Vores påstande om t er ikke lært af eksperimentelle ræsonnementer.

Vores påstande om t er ikke lært af logik eller matematik.

Vi har ikke viden om t.

Hvad betyder denne sætning “hvis og kun hvis”? Filosoffer mener, at den, og flere synonyme sætninger, bruges ofte i ræsonnementer. Hvis vi lader “hvis og kun” være uforklaret indtil videre, kan vi bruge følgende oversættelsesnøgle til at skrive argumentet op i en blanding af vores propositionelle logik og engelsk.

P: Vi har viden om t.

Q: Vores påstande om t er lært af eksperimentelle ræsonnementer.

R: Vores påstande om t er lært fra logik eller matematik.

Og så har vi:

P hvis og kun hvis (QvR)

¬Q

¬R

¬P

Vores opgave er at tilføje til vores logiske sprog en ækvivalent til “hvis og kun hvis”. Derefter kan vi evaluere denne omformulering af Humes argument.

9.2 Den bikonditionelle

Hvor vi introducerer et symbol synonymt med “hvis og kun hvis” og derefter udlægger dets syntaks og semantik, bør vi starte med en observation. En sætning som “P hvis og kun hvis Q” synes at være en forkortet måde at sige “P hvis Q og P kun hvis Q” på. Når vi først har bemærket dette, behøver vi ikke at forsøge at finde ud af, hvad “hvis og kun hvis” betyder, ved hjælp af vores ekspertforståelse af engelsk. I stedet kan vi finde ud af betydningen af “hvis og kun hvis” ved hjælp af vores allerede strenge definitioner af “hvis”, “og” og “kun hvis”. Konkret vil “P hvis Q og P kun hvis Q” blive oversat med “((Q→P)^(P→Q))”. (Hvis dette er uklart for dig, kan du gå tilbage og gennemgå afsnit 2.2.) Lad os nu lave en sandhedstabel for denne formel.

P	Q	(Q → P)	(P → Q)	((Q→P)^(P→Q))
T	T	T	T	T
T	F	T
T	F	F
F	T	F	T	F	F
F	T	F
F	F	T	T	T

Vi har afklaret semantikken for “hvis og kun hvis”. Vi kan nu indføre et nyt symbol for dette udtryk. Det er traditionelt at bruge den dobbelte pil, “↔”. Vi kan nu udtrykke syntaksen og semantikken for “↔”.

Hvis Φ og Ψ er sætninger, så

(Φ↔Ψ)

er en sætning. Denne type sætning kaldes typisk en “bikonditionel”.

Semantikken er givet ved følgende sandhedstabel.

Φ	Ψ	(Φ↔Ψ)
T	T	T
T	F	F
F	T
F	T	F
F	F	T

Et glædeligt resultat af vores redegørelse for bikonditionaliteten er, at den giver os mulighed for kortfattet at forklare det syntaktiske begreb om logisk ækvivalens. Vi siger, at to sætninger Φ og Ψ er “ækvivalente” eller “logisk ækvivalente”, hvis (Φ↔Ψ) er en sætning.

9.3 Alternative sætninger

På engelsk viser det sig, at der er flere sætninger, som normalt har samme betydning som bikonditionaliteten. Hver af de følgende sætninger ville blive oversat som (P↔Q).

P hvis og kun hvis Q.

P bare hvis Q.

P er nødvendig og tilstrækkelig for Q.

P er ækvivalent med Q.

9.4 Ræsonnement med bikonditionalen

Hvordan kan vi ræsonnere ved hjælp af en bikonditional? Umiddelbart ser det ud til at give lidt vejledning. Hvis jeg ved, at (P↔Q), ved jeg, at P og Q har samme sandhedsværdi, men ud fra den sætning alene ved jeg ikke, om de begge er sande eller begge er falske. Ikke desto mindre kan vi drage fordel af semantikken for bikonditionaliteten til at konstatere, at hvis vi også kender sandhedsværdien af en af de sætninger, der udgør bikonditionaliteten, kan vi udlede sandhedsværdien af den anden sætning. Dette giver anledning til at opstille et ligetil sæt regler. Der vil faktisk være tale om fire regler, men vi vil samle dem under et enkelt navn, “ækvivalens”:

og

og

og

Hvad nu, hvis vi i stedet forsøger at vise en bikonditionel? Her kan vi vende tilbage til den indsigt, at bikonditionaliteten (Φ↔Ψ) er ækvivalent med ((Φ→Ψ)^(Ψ→Φ)). Hvis vi kunne bevise både (Φ→Ψ) og (Ψ→Φ), vil vi vide, at (Φ↔Ψ) må være sandt.

Vi kan kalde denne regel for “bikondition”. Den har følgende form:

(Φ→Ψ)

(Ψ→Φ)

(Φ↔Ψ)

Det betyder, at vi ofte, når vi har til formål at bevise en bikonditionalitet, vil foretage to betingelsesafledninger for at udlede to betingelser og derefter bruge reglen om bikonditionalitet. Det vil sige, at mange beviser for bikonditionaler har følgende form:

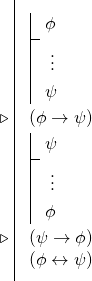
9.5 Tilbage til Hume

Vi kan nu se, om vi er i stand til at bevise Humes argument. Givet nu det nye bikonditionelle symbol, kan vi begynde et direkte bevis med vores tre præmisser.

Vi har allerede observeret, at vi mener, at (QvR) er falsk, fordi ¬Q og ¬R. Så lad os bevise ¬(QvR). Denne sætning kan ikke bevises direkte, da vi har de forudsætninger, vi har; og den kan ikke bevises med et betinget bevis, da den ikke er en betinget sætning. Så lad os prøve et indirekte bevis. Vi mener, at ¬(QvR) er sandt, så vi antager, at dette er benægtet, og viser en modsigelse.

Humes argument, i det mindste som vi har rekonstrueret det, er gyldigt.

Er Humes argument sundt? Om det er sundt afhænger af den første præmis ovenfor (da den anden og tredje præmis er abstraktioner om et eller andet emne t). Mere specifikt afhænger det af påstanden om, at vi har viden om noget, bare fordi vi kan vise det med eksperiment eller logik. Hume hævder, at vi bør have mistillid til – ja, vi bør brænde tekster, der indeholder – påstande, som ikke er baseret på eksperimenter og observationer eller på logik og matematik. Men tænk på denne påstand: Vi har viden om et emne t, hvis og kun hvis vores påstande om t er lært af eksperimenter eller vores påstande om t er lært af logik eller matematik.

Fandt Hume denne påstand gennem eksperimenter? Eller opdagede han den gennem logik? Hvilken skæbne ville Humes bog lide, hvis vi fulgte hans råd?

9.6 Nogle eksempler

Det kan være nyttigt at bevise nogle sætninger, der gør brug af det bikonditionelle, for at illustrere, hvordan vi kan ræsonnere med det bikonditionelle.

Her er et nyttigt princip. Hvis to sætninger har den samme sandhedsværdi som en tredje sætning, så har de den samme sandhedsværdi som hinanden. Vi angiver dette som ((((P↔Q)^(R↔Q))→(P↔R))). For at illustrere ræsonnementer med bikonditionaliteten, lad os bevise denne sætning.

Denne sætning er en konditionalitet, så den vil kræve en konditional afledning. Konsekvensen af den betingede er en bikonditional, så vi vil forvente at have brug for to betingede afledninger, en for at bevise (P→R) og en for at bevise (R→P). Beviset vil se således ud. Undersøg det nøje.

Vi har tidligere nævnt de principper, som vi forbinder med matematikeren Augustus De Morgan (1806-1871), og som i dag kaldes “De Morgans love” eller “De Morgan-ækvivalenterne”. Det drejer sig om erkendelsen af, at ¬(PvQ) og (¬P^¬Q) er ækvivalente, og også at ¬(P^Q) og (¬Pv¬Q) er ækvivalente. Vi kan nu udtrykke disse med bikonditionaliteten. Følgende er teoremer i vores logik:

(¬(PvQ)↔(¬P^¬Q))

(¬(P^Q)↔(¬Pv¬Q))

Vi vil bevise det andet af disse teoremer. Dette er måske det vanskeligste bevis, vi har set; det kræver indlejrede indirekte beviser, og en rimelig mængde snilde i at finde ud af, hvad den relevante modsigelse vil være.

9.7 Brug af sætninger

Hver sætning i vores logik er, semantisk set, en af tre slags sætninger. Den er enten en tautologi, en modsigelsessætning eller en kontingent sætning. Vi har allerede defineret “tautologi” (en sætning, der må være sand) og “modsigelsessætning” (en sætning, der må være falsk). En kontingent sætning er en sætning, som hverken er en tautologi eller en modsigelsessætning. En kontingent sætning er således en sætning, der kan være sand eller falsk.

Her er et eksempel på hver slags sætning:

(Pv¬P)

(P↔¬P)

P

Den første er en tautologi, den anden er en selvmodsigende sætning, og den tredje er kontingent. Vi kan se dette med en sandhedstabel.

P	¬P	(Pv¬P)	(P↔¬P)	P
T	F	T	F	T	F	T
F	T	T	T	F	F

Bemærk, at negationen af en tautologi er en modsigelse, at negationen af en modsigelse er en tautologi, og at negationen af en kontingent sætning er en kontingent sætning.

¬(Pv¬P)

¬(P↔¬P)

¬P

P	¬P	(Pv¬P)	¬(Pv¬P)	¬(Pv¬P)	¬(Pv¬P)	(P↔¬P)	¬(P↔¬P)
T	F	T	F	F	F	T	T
F	T	T	F	F	F	T

Et øjebliks eftertanke vil afsløre, at det ville være noget af en katastrofe, hvis enten en selvmodsigende sætning eller en kontingent sætning var en sætning i vores udsagnslogik. Vores logik blev designet til kun at producere gyldige argumenter. Argumenter, der ikke har nogen forudsætninger, bemærkede vi, bør have konklusioner, der må være sande (igen, dette følger af, at en sætning, der kan bevises uden forudsætninger, kan bevises med alle forudsætninger, og derfor må den hellere være sand, uanset hvilke forudsætninger vi bruger). Hvis en sætning var selvmodsigende, ville vi vide, at vi kunne bevise en usandhed. Hvis en sætning var kontingent, kunne vi nogle gange bevise en usandhed (dvs. vi kunne bevise en sætning, som under visse betingelser er falsk). Og eftersom vi har vedtaget indirekte afledning som bevismetode, følger det, at når vi først har en modsigelse eller en modsigelsesfuld sætning i et argument, kan vi bevise hvad som helst.

Sætninger kan være meget nyttige for os i argumenter. Lad os antage, at vi ved, at hverken Smith eller Jones vil tage til London, og at vi derfor ønsker at bevise, at Jones ikke vil tage til London. Hvis vi tillod os at bruge en af De Morgans sætninger, kunne vi hurtigt komme af med argumentet. Antag følgende nøgle:

P: Smith vil tage til London.

Q: Jones vil tage til London.

Og vi har følgende argument:

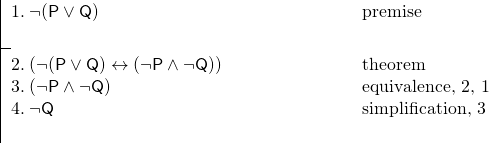
Dette bevis blev gjort meget let ved vores brug af sætningen i linje 2.

Der er to ting at bemærke ved dette. For det første bør vi tillade os selv at gøre dette, for hvis vi ved, at en sætning er en sætning, så ved vi, at vi kan bevise denne sætning i et underbevis. Det vil sige, at vi kunne erstatte linje 2 ovenfor med en lang underbevis, der beviser (¬(P v Q)↔(¬P ^ ¬Q))), som vi så kunne bruge. Men hvis vi er sikre på, at (¬(P v Q)↔(¬P ^ ¬Q))) er en sætning, burde vi ikke behøve at lave dette bevis igen og igen, hver gang vi ønsker at gøre brug af sætningen.

Det andet problem, som vi bør erkende, er mere subtilt. Der findes uendeligt mange sætninger af samme form som vores sætning, og vi burde også kunne bruge dem. For eksempel ville følgende sætninger hver især have et bevis, der er identisk med vores bevis for sætningen (¬(P v Q)↔(¬P ^ ¬Q))), bortset fra at bogstaverne ville være forskellige:

(¬(R v S) ↔ (¬R ^ ¬S))

(¬(T v U) ↔ (¬T ^ ¬U))

(¬(V v W) ↔ (¬V ^ ¬W))

Dette er forhåbentlig indlysende. Tag beviset for (¬(P v Q)↔(¬P ^ ¬Q)), og erstat i dette bevis hver forekomst af P med R og hver forekomst af Q med S, og du vil have et bevis for (¬(R v S)↔(¬R ^ ¬S)).

Men her er noget, der måske er mindre indlysende. Hver af de følgende kan opfattes som svarende til sætningen (¬(P v Q)↔(¬P ^ ¬Q)).

(¬((P^Q) v (R^S))↔(¬(P^Q) ^ ¬(R^S)))

(¬(T v (Q v (Q v V))↔(¬T ^ ¬(Q v V))

(¬((Q↔P) v (¬R→¬Q))↔(¬(Q↔P) ^ ¬(¬(¬R→¬Q)))

For eksempel, hvis man tog et bevis for (¬(P v Q)↔(¬(P ^ ¬Q))) og erstattede hver indledende instans af P med (Q↔P) og hver indledende instans af Q med (¬R→¬Q), så ville man have et bevis for sætningen (¬((Q↔P) v (¬R→¬Q))↔(¬(Q↔P) ^ ¬(¬(¬R→¬Q)))).

Vi kunne indfange denne indsigt på to måder. Vi kunne opstille sætninger i vores metasprog og tillade, at disse har forekomster. Vi kunne således tage (¬(Φ v Ψ) ↔ (¬Φ ^ ¬Ψ)) som en sætning i metasproget, hvor vi kunne erstatte hver Φ med en sætning og hver Ψ med en sætning og få en bestemt forekomst af en sætning. Et alternativ er at tillade, at vi ud fra en sætning kan frembringe andre sætninger gennem substitution. For nemheds skyld vil vi vælge denne anden strategi.

Vores regel vil være denne. Når vi først har bevist en sætning, kan vi til enhver tid citere den i et bevis. Vores begrundelse er, at påstanden er et teorem. Vi tillader substitution af enhver atomar sætning i sætningen med en hvilken som helst anden sætning, hvis og kun hvis vi erstatter hver indledende forekomst af den atomare sætning i sætningen med den samme sætning.

Hvor vi ser på et eksempel, er det gavnligt at opremse nogle nyttige sætninger. Der findes uendeligt mange teoremer i vores sprog, men disse ti er ofte meget nyttige. Et par stykker har vi bevist. De andre kan bevises som en øvelse.

T1 (P v ¬P)

T2 (¬(P→Q) ↔ (P^¬Q))

T3 (¬(P v Q) ↔ (¬P ^ ¬Q))

T4 ((¬P v ¬Q) ↔ ↔ ¬(P ^ Q))

T5 (¬(P ↔ Q) ↔ (P ↔ ¬Q))

T6 (¬P → (P → Q))

T7 (P → (Q → P))

T8 ((P→(Q→R)) → ((P→Q) → (P→R)))

T9 ((¬P→¬Q) → ((¬P→Q) →P))

T10 ((P→Q) → (¬Q→¬P))

Nogle eksempler vil gøre fordelen ved at bruge sætninger klart. Overvej et andet argument, der bygger på det ovenstående. Vi ved, at det hverken er tilfældet, at hvis Smith tager til London, vil han tage til Berlin, eller at det er tilfældet, at hvis Jones tager til London, vil han tage til Berlin. Vi ønsker at bevise, at det ikke er tilfældet, at Jones vil rejse til Berlin. Vi tilføjer følgende til vores nøgle:

R: Smith vil rejse til Berlin.

S: Jones vil tage til Berlin.

Og vi har følgende argument:

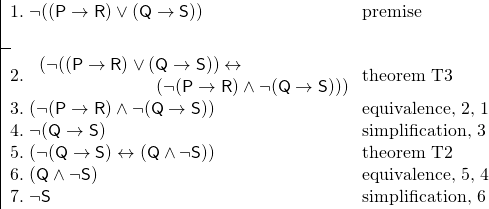
Ved hjælp af sætninger er dette bevis blevet meget kortere, end det ellers ville være blevet. Desuden gør sætninger ofte et bevis lettere at følge, da vi genkender sætningerne som tautologier – som sætninger, der må være sande.

9.8 Problemer

1. Bevis, at hvert af følgende argumenter er gyldigt.

1. Præmisser: P, ¬Q. Konklusion: Konklusion: ¬(P↔Q).
2. Præmisser: (¬PvQ), (Pv¬Q). Konklusion: (P↔Q).
3. Præmisser: (P↔Q).
4. Præmisser: (P↔Q), (R↔S) . Konklusion: ((P^R)↔(Q^S))).

1. Bevis hver af følgende sætninger.

1. T1
2. T2
3. T5
4. T6
5. T7
6. T8
7. T9
8. ((P^Q)↔¬(¬Pv¬Q))
9. ((P→Q)↔¬(P^¬Q))

1. Skriv på almindeligt talesprog dit eget gyldige argument med mindst to præmisser, hvoraf mindst én er en bikonditional. Dit argument skal blot være et afsnit (ikke en ordnet liste af sætninger eller noget andet, der ligner formel logik). Oversæt det til udsagnslogik og bevis, at det er gyldigt.
2. Skriv på almindeligt dagligdags engelsk dit eget gyldige argument med mindst to præmisser og med en konklusion, der er en bikonditionel. Dit argument skal blot være et afsnit (ikke en ordnet liste af sætninger eller noget andet, der ser formelt ud som logik). Oversæt det til udsagnslogik, og bevis, at det er gyldigt.