Uma Introdução Concisa à Lógica

9.1 Um exemplo histórico

O filósofo David Hume (1711-1776) é lembrado por ser um brilhante empírico cético. Uma pessoa é céptica em relação a um tópico se essa pessoa tem padrões muito rígidos para o que constitui conhecimento sobre esse tópico e também acredita que não podemos atender a esses padrões rígidos. Empirismo é a visão de que nós ganhamos conhecimento principalmente através da experiência, experiências particulares dos nossos sentidos. Em seu livro, An Inquiry Concerning Human Understanding, Hume expõe seus princípios para o conhecimento, e depois nos aconselha a limpar nossas bibliotecas:

Quando atropelamos bibliotecas, persuadidos desses princípios, que caos devemos fazer? Se tomarmos em nossas mãos qualquer volume de divindade ou metafísica escolar, por exemplo, vamos perguntar: Contém algum raciocínio abstrato sobre quantidade ou número? Não. Contém algum raciocínio experimental a respeito da matéria de fato e existência? Não. Comprometa-o então com as chamas, pois não pode conter nada além de sofisma e ilusão.

Hume sentiu que as únicas fontes de conhecimento eram o raciocínio lógico ou matemático (que ele chama acima de “raciocínio abstrato a respeito da quantidade ou número”) ou a experiência dos sentidos (“raciocínio experimental a respeito da matéria de fato e existência”). Hume é levado a argumentar que qualquer afirmação não baseada em um ou outro método é inútil.

Nós podemos reconstruir o argumento de Hume da seguinte maneira. Suponha que t é algum tópico sobre o qual afirmamos ter conhecimento. Suponhamos que não obtivemos esse conhecimento por experiência ou lógica. Escrito em inglês, podemos reconstruir seu argumento da seguinte forma:

Temos conhecimento sobre t se e somente se nossas afirmações sobre t forem aprendidas do raciocínio experimental ou da lógica ou matemática.

As nossas afirmações sobre t não são aprendidas do raciocínio experimental.

As nossas afirmações sobre t não são aprendidas da lógica ou da matemática.

Não temos conhecimento sobre t.

O que significa essa frase “se e só se”? Os filósofos pensam que ela, e várias frases sinônimas, são usadas com freqüência no raciocínio. Deixando “se e só” inexplicado por enquanto, podemos usar a seguinte chave de tradução para escrever o argumento em uma mistura de nossa lógica proposicional e inglês.

P: Temos conhecimento sobre t.

Q: Nossas afirmações sobre t são aprendidas do raciocínio experimental.

R: Nossas afirmações sobre t são aprendidas com lógica ou matemática.

E assim temos:

P se e somente se (QvR)

¬Q

¬R

>P

Nossa tarefa é adicionar à nossa linguagem lógica um equivalente a “se e somente se”. Então podemos avaliar esta reformulação do argumento de Hume.

9.2 O biconditional

Antes de introduzirmos um símbolo sinônimo de “se e somente se”, e depois expormos sua sintaxe e semântica, devemos começar com uma observação. Uma frase como “P if e only if Q” parece ser uma forma abreviada de dizer “P if Q e P only if Q”. Uma vez que percebemos isso, não temos de tentar discernir o significado de “se e só se” usando o nosso conhecimento especializado de inglês. Em vez disso, podemos discernir o significado de “se e só se” usando as nossas já rigorosas definições de “se”, “and”, e “só se”. Especificamente, “P if Q e P only if Q” será traduzido “((Q→P)^(P→Q))”. (Se isto não estiver claro para si, volte atrás e reveja a secção 2.2.) Agora, vamos fazer uma tabela da verdade para esta fórmula.

P	Q	(Q → P)	(P → Q)	((→)^(→))
T	T	T	T	T
T	F	T	F	F
F	T	F	T	F	F
F	F	T	T	T

Passamos a semântica para “se e só se”. Podemos agora introduzir um novo símbolo para esta expressão. É tradicional usar a seta dupla, “↔”. Podemos agora expressar a sintaxe e semântica de “↔”.

Se Φ e Ψ são frases, então

(Φ↔Ψ)

é uma frase. Este tipo de frase é normalmente chamada de “biconditional”.

A semântica é dada pela seguinte tabela de verdade.

Φ	Φ↔Ψ	(Φ↔Ψ)
T	T	T
T	F	F
F	T	F
F	F	T

Um resultado agradável do nosso relato do biconditional é que ele nos permite explicar sucintamente a noção sintáctica de equivalência lógica. Dizemos que duas frases Φ e Ψ são “equivalentes” ou “logicamente equivalentes” se (Φ↔Ψ) for um teorema.

9.3 Frases alternativas

Em inglês, parece que há várias frases que normalmente têm o mesmo significado que o bicondicional. Cada uma das frases seguintes seria traduzida como (P↔Q).

P se e somente se Q.

P apenas no caso de Q.

P ser necessário e suficiente para Q.

P é equivalente a Q.

9.4 Raciocínio com o bicondicional

Como podemos raciocinar usando um bicondicional? A princípio, parece oferecer pouca orientação. Se eu sei disso (P↔Q), eu sei que P e Q têm o mesmo valor de verdade, mas só por essa frase eu não sei se ambos são verdadeiros ou ambos falsos. No entanto, podemos tirar vantagem da semântica para o biconditional para observar que se também sabemos o valor verdadeiro de uma das frases que constituem o biconditional, então podemos derivar o valor verdadeiro da outra frase. Isto sugere um conjunto de regras simples. Na verdade, serão quatro regras, mas vamos agrupá-las sob um único nome, “equivalência”:

e

e

e

E se em vez disso estivermos a tentar mostrar um biconditional? Aqui podemos voltar ao insight de que o biconditional (Φ↔Ψ) é equivalente a ((Φ→Ψ)^(Ψ→Φ)). Se pudéssemos provar ambos (Φ→Ψ) e (Ψ→Φ), saberíamos que (Φ↔Ψ) deve ser verdadeiro.

Podemos chamar esta regra de “bicondição”. Ela tem a seguinte forma:

(Φ→Ψ)

(Ψ→Φ)

(Φ↔Ψ)

Isto significa que, muitas vezes, quando pretendemos provar uma bicondição, iremos empreender duas derivações condicionais para derivar duas condições, e então usaremos a regra da bicondição. Ou seja, muitas provas de bicondicionais têm a seguinte forma:

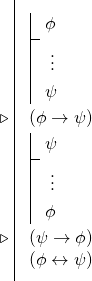
9.5 Voltando a Hume

Agora podemos ver se somos capazes de provar o argumento de Hume. Dado agora o novo símbolo biconditional, podemos começar uma prova directa com as nossas três premissas.

Já observámos que pensamos (QvR) que é falso porque ¬Q e ¬R. Portanto, vamos provar ¬(QvR). Esta frase não pode ser provada diretamente, dadas as premissas que temos; e não pode ser provada com uma prova condicional, uma vez que não é uma condicional. Portanto, vamos tentar uma prova indirecta. Acreditamos que ¬(QvR) é verdade, então vamos assumir a negação disto e mostrar uma contradição.

O argumento do Hume, pelo menos enquanto o reconstruímos, é válido.

O argumento do Hume é válido? Se é som depende da primeira premissa acima (já que a segunda e terceira premissas são abstrações sobre algum tópico t). Mais especificamente, depende da afirmação de que temos conhecimento sobre algo, no caso de o podermos mostrar com experiência ou lógica. Hume argumenta que devemos desconfiar – na verdade, devemos queimar textos contendo reivindicações que não sejam de experimento e observação, ou de lógica e matemática. Mas considere esta afirmação: nós temos conhecimento sobre um tópico t se e somente se nossas afirmações sobre t forem aprendidas com experimento ou nossas afirmações sobre t forem aprendidas com lógica ou matemática.

Did Hume descobre esta afirmação através de experimentos? Ou ele a descobriu através da lógica? Que destino sofreria o livro de Hume, se seguíssemos seu conselho?

9.6 Alguns exemplos

Pode ser útil provar alguns teoremas que fazem uso do bicondicional, a fim de ilustrar como podemos raciocinar com o bicondicional.

Aqui está um princípio útil. Se duas frases têm o mesmo valor de verdade de uma terceira frase, então elas têm o mesmo valor de verdade uma da outra. Nós dizemos isto como (((P↔Q)^(R↔Q))→(P↔R)). Para ilustrar o raciocínio com o bicon condicional, vamos provar este teorema.

Este teorema é um condicional, portanto, ele vai requerer uma derivação condicional. O conseqüente do condicional é um biconcondicional, então esperaremos precisar de duas derivações condicionais, uma para provar (P→R) e outra para provar (R→P). A prova terá este aspecto. Estude-a de perto.

Mencionamos antes os princípios que associamos ao matemático Augustus De Morgan (1806-1871), e que hoje são chamados de “Leis De Morgan” ou “Equivalências De Morgan”. Estes são o reconhecimento de que ¬(PvQ) e (P^Q) são equivalentes, e também que ¬(P^Q) e (PvQ) são equivalentes. Podemos agora expressá-los com o biconditional. Os seguintes são teoremas da nossa lógica:

(¬(PvQ)↔(¬P^¬Q))

(¬(P^Q)↔(¬Pv¬Q))

Provaremos o segundo destes teoremas. Esta é talvez a prova mais difícil que já vimos; requer provas indiretas aninhadas, e uma boa quantidade de esperteza em encontrar qual será a contradição relevante.

9.7 Usando teoremas

Cada frase da nossa lógica é, em termos semânticos, um de três tipos. Ou é uma tautologia, uma frase contraditória, ou uma frase contingente. Já definimos “tautologia” (uma frase que deve ser verdadeira) e “frase contraditória” (uma frase que deve ser falsa). Uma frase contingente é uma frase que não é uma tautologia, nem uma frase contraditória. Assim, uma frase contingente é uma frase que pode ser verdadeira, ou pode ser falsa.

Aqui está um exemplo de cada tipo de frase:

(Pv¬P)

(P↔¬P)

P

A primeira é uma tautologia, a segunda é uma frase contraditória, e a terceira é contingente. Podemos ver isto com uma tabela de verdade.

P	>P	(Pv¬P)	(P↔¬P)	P
T	F	T	F	F	T
F	T	T	F	F

Notem que a negação de uma tautologia é uma contradição, a negação de uma contradição é uma tautologia, e a negação de uma sentença contingente é uma sentença contingente.

>(Pv¬P)

>(P↔¬P)

>>P

P	>(Pv¬P)	(Pv¬P)	>(Pv¬P)	(P↔¬P)	>(P↔¬P)
T	F	T	T	F	F	T
F	T	T	F	F	T

Um momento de reflexão revelará que seria um desastre se uma frase contraditória ou uma frase contingente fosse um teorema da nossa lógica proposicional. A nossa lógica foi concebida para produzir apenas argumentos válidos. Argumentos que não têm premissas, observamos, devem ter conclusões que devem ser verdadeiras (mais uma vez, isto se segue porque uma frase que não pode ser provada sem premissas pode ser provada com qualquer premissas, e por isso é melhor que seja verdade independentemente das premissas que utilizamos). Se um teorema fosse contraditório, saberíamos que poderíamos provar uma falsidade. Se um teorema fosse contingente, então algumas vezes poderíamos provar uma falsidade (ou seja, poderíamos provar uma sentença que é, sob algumas condições, falsa). E, dado que adotamos a derivação indireta como método de prova, segue-se que uma vez que temos uma contradição ou uma frase contraditória em um argumento, podemos provar qualquer coisa.

Os teoremas podem ser muito úteis para nós em argumentos. Suponhamos que sabemos que nem Smith nem Jones irão a Londres, e queremos provar, portanto, que Jones não irá a Londres. Se nos permitíssemos usar um dos teoremas de De Morgan, poderíamos fazer um trabalho rápido do argumento. Suponha a seguinte chave.

P: Smith irá para Londres.

Q: Jones irá para Londres.

E temos o seguinte argumento:

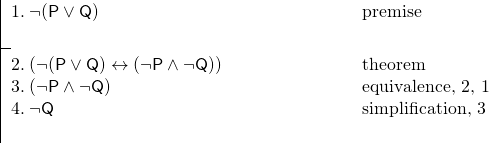
Esta prova foi feita muito facilmente pelo nosso uso do teorema na linha 2.

Existem duas coisas a notar sobre isto. Primeiro, devemos nos permitir fazer isso, porque se sabemos que uma frase é um teorema, então sabemos que podemos provar que o teorema em uma sub-prova. Ou seja, poderíamos substituir a linha 2 acima por uma longa sub-prova que prova (¬(P v Q)↔(¬P ^ ¬Q)), que depois poderíamos utilizar. Mas se tivermos a certeza que (¬(P v Q)↔(¬P ^ ^ ¬Q)) é um teorema, não devemos precisar de fazer esta prova repetidamente, cada vez que queremos fazer uso do teorema.

O segundo número que devemos reconhecer é mais subtil. Há infinitas frases da forma do nosso teorema, e devemos ser capazes de usá-las também. Por exemplo, as frases seguintes teriam cada uma uma prova idêntica à nossa prova do teorema (¬(P v Q)↔(¬P ^ ¬Q)), exceto que as letras seriam diferentes:

(¬(R v S) ↔ (¬R ^ ¬S))

(¬(T v U) ↔ (¬T ^ ¬U))

(¬(V v W) ↔ (¬V ^ ¬W))

Esperemos que isto seja óbvio. Pegue a prova de (¬(P v Q)↔(¬P ^ ¬Q)), e nessa prova substitua cada instância de P por R e cada instância de Q por S, e você teria uma prova de (¬(R v S)↔(¬R ^ ¬S)).

Mas aqui está algo que talvez seja menos óbvio. Cada uma das seguintes coisas pode ser considerada como semelhante ao teorema (¬(P v Q)↔(¬P ^ ^ ¬Q)).

(¬((P^Q) v (R^S))↔(¬(P^Q) ^ ¬(R^S)))

(¬(T v v (Q v V))↔(¬T ^ ¬(Q v V))

(¬((Q↔P) v (¬COPY14¬Q))↔(¬(Q↔P) ^ ¬(¬COPY14¬Q))

Por exemplo, se se pegar uma prova de (¬(P v Q)↔(¬P ^ ¬Q)) e substituir cada instância inicial de P por (Q↔P) e cada instância inicial de Q por (¬COPY14¬Q), então teríamos uma prova do teorema (¬((Q↔P) v (¬COPY14¬Q))↔(¬(Q↔P) ^ ^(¬COPY14¬Q))).

Podemos captar esta percepção de duas maneiras. Poderíamos afirmar teoremas de nossa metalinguagem e permitir que estes tenham instâncias. Assim, poderíamos tomar (¬(Φ v Ψ) ↔ (¬COPY18 ^ ¬COPY5)) como um teorema da metalinguagem, no qual poderíamos substituir cada Φ por uma frase e cada Ψ por uma frase e obter uma instância particular de um teorema. Uma alternativa é permitir que a partir de um teorema possamos produzir outros teoremas através da substituição. Para facilitar, tomaremos esta segunda estratégia.

A nossa regra será esta. Uma vez que provemos um teorema, podemos citá-lo em uma prova a qualquer momento. A nossa justificação é que a reivindicação é um teorema. Nós permitimos a substituição de qualquer frase atômica no teorema por qualquer outra frase se e somente se substituirmos cada instância inicial dessa frase atômica no teorema pela mesma frase.

Antes de considerarmos um exemplo, é benéfico listar alguns teoremas úteis. Existem infinitamente muitos teoremas da nossa linguagem, mas estes dez são muitas vezes muito úteis. Alguns nós já provamos. Os outros podem ser provados como um exercício.

T1 (P v ¬P)

T2 (¬(P→Q) ↔ (P^¬Q))

T3 (¬(P v Q) ↔ (¬P ^ ¬Q))

T4 ((¬P v ¬Q) ↔ ¬(P ^ Q))

T5 (¬(P ↔ Q) ↔ (P ↔ ¬Q))

T6 (¬P → (P → Q))

T7 (P → (Q → P))

T8 ((P→(Q→R)) → ((P→Q) → (P→R)))

T9 ((¬P→¬Q) → ((¬P→Q) →P))

T10 ((P→Q) → (¬Q→¬P))

Alguns exemplos tornarão clara a vantagem de utilizar os teoremas. Considere um argumento diferente, partindo do acima. Sabemos que não é o caso que se Smith for para Londres, ele irá para Berlim, nem é o caso que se Jones for para Londres, ele irá para Berlim. Nós queremos provar que não é o caso de Jones ir a Berlim. Adicionamos o seguinte à nossa chave:

R: Smith irá a Berlim.

S: Jones irá a Berlin.

E temos o seguinte argumento:

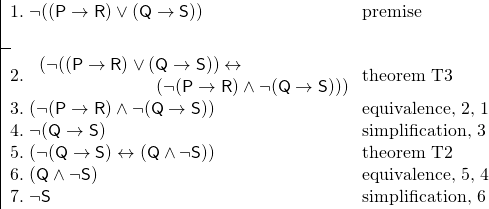
Usar teoremas fez esta prova muito mais curta do que poderia ser de outra forma. Além disso, os teoremas frequentemente tornam uma prova mais fácil de seguir, já que reconhecemos os teoremas como tautologias – como frases que devem ser verdadeiras.

9.8 Problemas

1. Prove que cada um dos seguintes argumentos é válido.

1. Premises: P, ¬Q. Conclusão: ¬(P↔Q).
2. Premises: (¬PvQ), (Pv¬Q). Conclusão: (P↔Q).
3. Premises: (P↔Q), (R↔S) . Conclusão: ((P^R)↔(Q^S)).

1. Prove cada um dos seguintes teoremas.

1. T1
2. T2
3. T5
4. T6
5. T7
6. T8
7. T9
8. ((P^Q)↔¬(¬Pv¬Q))
9. ((↔)↔¬(P^¬Q))

1. Em inglês coloquial normal, escreva o seu próprio argumento válido com pelo menos duas premissas, das quais pelo menos uma é bicondicional. Seu argumento deve ser apenas um parágrafo (não uma lista ordenada de frases ou qualquer outra coisa que se pareça com lógica formal). Traduza-o em lógica proposicional e prove que é válido.
2. Em inglês coloquial normal, escreva seu próprio argumento válido com pelo menos duas premissas, e com uma conclusão que seja bicondicional. Seu argumento deve ser apenas um parágrafo (e não uma lista ordenada de frases ou qualquer outra coisa que pareça formal como lógica). Traduza-o em lógica proposicional e prove que é válido.