Proton

Nutronens sönderfall

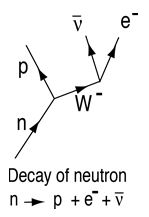
En fri neutron sönderfaller med en halveringstid på cirka 10,3 minuter, men den är stabil om den kombineras med en atomkärna. Detta sönderfall är ett exempel på betasönderfall med emission av en elektron och en elektronantineutrino. Neutronens sönderfall involverar den svaga växelverkan, vilket framgår av Feynman-diagrammet till höger.

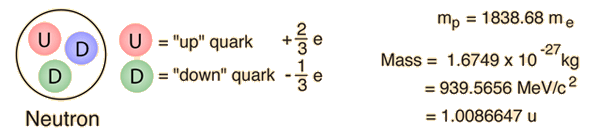
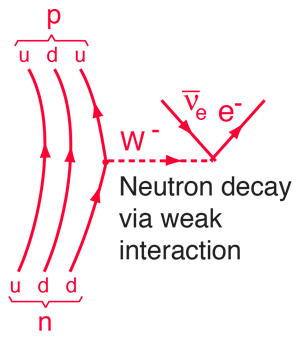Ett mer detaljerat diagram över neutronens sönderfall identifierar det som en omvandling av en av neutronens ner-kvarkar till en upp-kvark. Det är ett exempel på den typ av kvarktransformationer som är inblandade i många kärnprocesser, inklusive betasönderfall.

Nutronens sönderfall är ett bra exempel på de observationer som ledde till upptäckten av neutrino. En analys av energin i sönderfallet kan användas för att illustrera de dilemman som de tidiga forskarna av denna process stod inför.

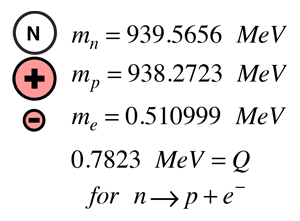Med hjälp av begreppet bindningsenergi, och genom att representera partiklarnas massor med deras vilomassaenergier, kan energiutbytet från neutronsönderfallet beräknas utifrån partikelmassorna. Energiutbytet representeras traditionellt av symbolen Q. Eftersom energi och rörelsemängd måste bevaras vid sönderfallet kommer det att visas att den lättare elektronen kommer att bära med sig det mesta av den kinetiska energin. Med en kinetisk energi av denna storlek måste det relativistiska uttrycket för kinetisk energi användas.

För tillfället antar vi (felaktigt) att sönderfallet endast omfattar proton och elektron som produkter. Energiutbytet Q skulle då delas mellan proton och elektron. Elektronen kommer att få den största delen av den kinetiska energin och kommer att vara relativistisk, men protonen är icke-relativistisk. Energibalansen är då

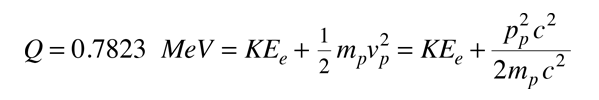
I neutronens viljeläge, krävs för att bevara rörelsemängden

pcelectron = – pcproton

och pcelectron kan uttryckas i termer av elektronens rörelseenergi

.

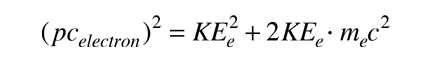Visa

Energibalansen blir då

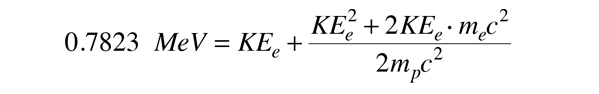
När du ersätter siffrorna för detta värde på Q, ser man att termen KEe2 är försumbar, så elektronens erforderliga rörelseenergi kan beräknas. Den erforderliga kinetiska energin hos elektronen för detta tvåpartikelsjukdomsschema är

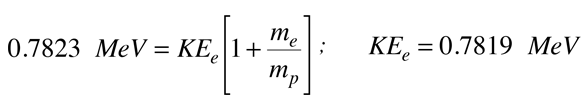
På samma sätt tvingas elektronens rörelsemängd för detta tvåpartikelsjukdomsschema att vara

Rörelsemängden och energin för tvåpartikelsjukdomsschemat tvingas till dessa värden, men så beter sig inte naturen. De observerade fördelningarna av impuls och energi för elektronen är som visas nedan.

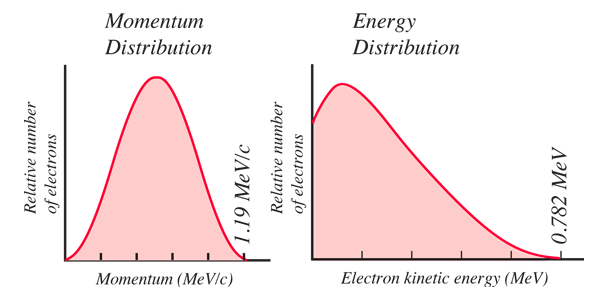
Det faktum att de elektroner som producerades från neutronernas sönderfall hade kontinuerliga fördelningar av energi och impuls var en tydlig indikation på att det fanns ytterligare en partikel som emitterades tillsammans med elektronen och protonen. Den måste vara en neutral partikel och i vissa sönderfall bar den nästan all energi och rörelsemängd från sönderfallet. Detta skulle inte ha varit så märkligt om det inte vore för det faktum att när elektronen hade sin maximala rörelseenergi stod den för all den energi Q som var tillgänglig för sönderfallet. Det fanns alltså ingen energi kvar för att ta hänsyn till massanergin hos den andra emitterade partikeln. De tidiga experimenterarna stod inför dilemmat med en partikel som kunde bära nästan all energi och impuls från sönderfallet men som inte hade någon laddning och uppenbarligen ingen massa!

Den mystiska partikeln kallades neutrino, men det dröjde tjugofem år innan en entydig experimentell observation av neutrino gjordes av Cowan och Reines. Den nuvarande förståelsen av neutronens sönderfall är

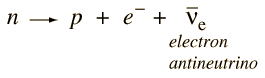
Detta sönderfall illustrerar några av de bevarandelagar som styr partikelers sönderfall. Protonen i produkten uppfyller bevarandet av baryonantalet, men elektronens uppkomst utan sällskap skulle bryta mot bevarandet av leptonantalet. Den tredje partikeln måste vara en elektronantineutrino för att sönderfallet ska kunna uppfylla bevarandet av leptonantalet. Elektronen har leptontal 1 och antineutrino har leptontal -1.

Experimentell detektion av neutriner

Stabilitet hos neutronen i deuteronen

.