En satellit är en kropp som rör sig runt en annan kropp i en matematiskt förutsägbar bana som kallas bana. En kommunikationssatellit är inget annat än en mikrovågsrepeaterstation i rymden som är till hjälp inom telekommunikation, radio och tv tillsammans med internettillämpningar.
En repeater är en krets som ökar styrkan på den signal den tar emot och återutsänder den. Men här fungerar denna repeater som en transponder, som ändrar frekvensbandet för den överförda signalen, från den mottagna.
Frekvensen med vilken signalen skickas ut i rymden kallas Uplink-frekvens, medan frekvensen med vilken den sänds av transpondern är Downlink-frekvensen.
Den följande figuren illustrerar detta begrepp tydligt.
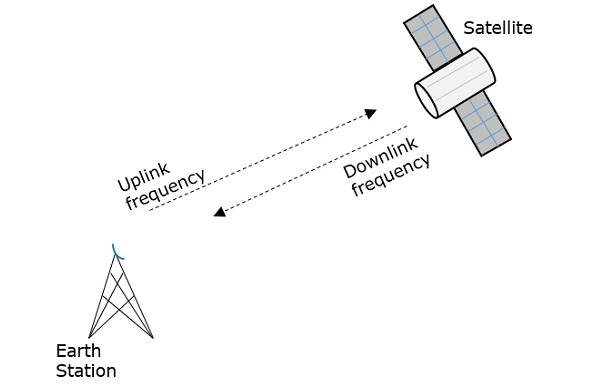
Nu ska vi titta på fördelarna, nackdelarna och tillämpningarna av satellitkommunikation.
Satellitkommunikation – Fördelar
Det finns många fördelar med satellitkommunikation såsom –
-
Flexibilitet
-
Lätt att installera nya kretsar
-
Distanserna kan lätt överbryggas och kostnaden spelar ingen roll
-
Sändningar. möjligheter
-
Varje hörn av jorden täcks
-
Användaren kan styra nätverket
Satellitkommunikation – Nackdelar
Satellitkommunikation har följande nackdelar –
-
Den initiala kostnaden, t.ex. segment- och uppskjutningskostnad, är för hög.
-
Frekvensstockning
-
Interferens och utbredning
Satellitkommunikation – Tillämpningar
Satellitkommunikation finner sina tillämpningar inom följande områden –
-
I radiosändningar.
-
I TV-sändningar såsom DTH.
-
I Internettillämpningar såsom tillhandahållande av Internetanslutning för dataöverföring, GPS-tillämpningar, Internetsurfning osv.
-
För röstkommunikation.
-
För forskning och utveckling inom många områden.
-
För militära tillämpningar och navigering.
Satellitens orientering i sin omloppsbana beror på de tre lagar som kallas Keplers lagar.
Keplers lagar
Astronomen Johannes Kepler (1571-1630) gav tre revolutionerande lagar om satelliters rörelse. Den bana som en satellit följer runt sin primärpunkt (jorden) är en ellips. Ellipsen har två brännpunkter – F1 och F2, varav jorden är den ena.
Om avståndet från objektets centrum till en punkt på dess elliptiska bana beaktas, kallas den längsta punkten i en ellips från centrum för apogee och den kortaste punkten i en ellips från centrum för perigee.
Keplers första lag
Keplers första lag säger att ”varje planet kretsar runt solen i en elliptisk bana, med solen som ett av dess fokus”. En satellit rör sig således i en elliptisk bana med jorden som ett av sina fokus.
Ellipsens halva huvudaxel betecknas som ”a” och halva lilla axeln betecknas som b. Därför kan excentriciteten e för detta system skrivas som –
$$$e = \frac{\sqrt{a^{2}-b^{2}}}}{a}$$$$
-
Excentricitet (e) – Det är den parameter som definierar skillnaden i ellipsens form i förhållande till en cirkels.
-
Semi-majoraxel (a) – Det är den längsta diametern som dras mellan de två brännpunkterna längs centrum, och som berör båda apogeerna (de mest avlägsna punkterna i en ellips från centrum).
-
Semimindre axel (b) – Det är den kortaste diametern som dras genom centrum och som berör båda perigeerna (de kortaste punkterna i en ellips från centrum).
Dessa beskrivs väl i följande figur.
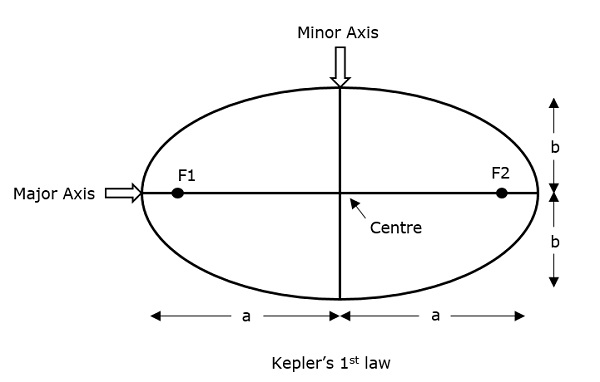
För en elliptisk bana är det alltid önskvärt att excentriciteten ska ligga mellan 0 och 1, dvs.Dvs. 0 < e < 1, för om e blir noll kommer banan inte längre att vara elliptisk utan snarare omvandlas till en cirkulär bana.
Keplers andra lag
Keplers andra lag säger att: ”För lika långa tidsintervaller är det område som täcks av satelliten lika stort med avseende på jordens centrum.”
Det kan förstås genom att ta en titt på följande figur.
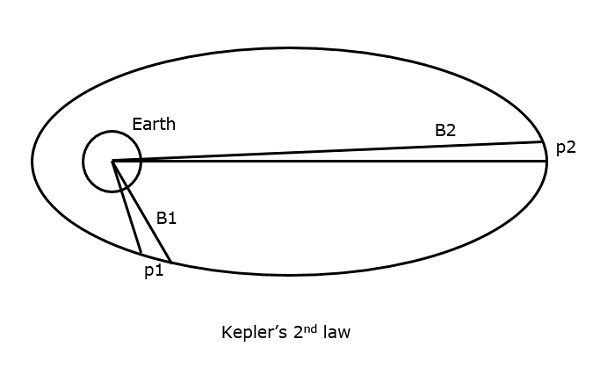
Antag att satelliten täcker p1 och p2 avstånd, under samma tidsintervall, så är de areor B1 och B2 som täcks i båda fallen respektive lika stora.
Keplers tredje lag
Keplers tredje lag säger att: ”Kvadraten av banans periodiska tid är proportionell mot kuben av medelavståndet mellan de två kropparna.”
Detta kan skrivas matematiskt som
$$$T^{2}\:\alpha\:\:a^{3}$$$
Vilket innebär
$$$T^{2} = \frac{4\pi ^{2}}{GM}a^{3}$$$
Varvid $\frac{4\pi ^{2}}{GM}$ är proportionalitetskonstanten. (enligt Newtons mekanik)
$$$T^{2} = \frac{4\pi ^{2}}}{\mu}a^{3} $$
Har μ = jordens geocentriska gravitationskonstant, i.dvs. Μ = 3.986005 × 1014 m3/sek2
$$1 = \left ( \frac{2\pi}{T} \right )^{2}\frac{a^{3}}{\mu}$$
$$$1 = n^{2}\frac{a^{3}}{\mu}\:\:\:\:\Rightarrow \:\:\:\:a^{3} = \frac{\mu}{n^{2}}}$$$
Varvid n = satellitens medelrörelse i radianer per sekund
Satelliternas omloppsfunktion beräknas med hjälp av dessa Keplers lagar.
Samtidigt med dessa finns det en viktig sak som måste noteras. En satellit, när den kretsar runt jorden, utsätts för en dragkraft från jorden som är gravitationskraften. Dessutom upplever den en viss dragkraft från solen och månen. Det finns alltså två krafter som verkar på den. De är –
-
Centripetalkraft – Den kraft som tenderar att dra ett föremål som rör sig i en bana mot sig själv kallas centripetalkraft.
-
Centrifugalkraft – Den kraft som tenderar att trycka ett föremål som rör sig i en bana bort från sin position kallas centrifugalkraft.
En satellit måste alltså balansera dessa två krafter för att hålla sig i sin omloppsbana.
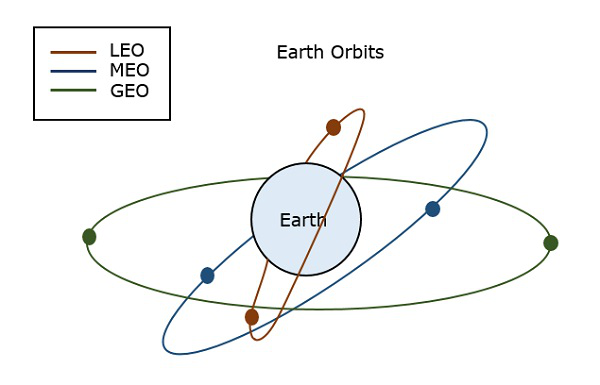
Jordbanor
En satellit som skjuts upp i rymden måste placeras i en viss omloppsbana för att ge ett visst sätt för sin revolution, så att den kan bibehålla tillgängligheten och tjäna sitt syfte, vare sig det är vetenskapligt, militärt eller kommersiellt. Sådana banor som tilldelas satelliter i förhållande till jorden kallas jordbanor. Satelliterna i dessa banor är jordbanesatelliter.
De viktiga typerna av jordbanor är –
-
Geosynkrona jordbanor
-
Medelhög jordbana
-
Låg jordbana
Geosynkrona jordbanesatelliter
En geo-.Synkrona jordomloppsbana (GEO) är en satellit som är placerad på en höjd av 22,300 miles över jorden. Denna omloppsbana är synkroniserad med en sida verklig dag (dvs. 23 timmar och 56 minuter). Denna bana kan ha en lutning och excentricitet. Den får inte vara cirkulär. Denna bana kan vara lutande vid jordens poler. Men den verkar stationär när den observeras från jorden.
Den samma geosynkrona omloppsbana, om den är cirkulär och ligger i ekvatorplanet, kallas för geostationär omloppsbana. Dessa satelliter är placerade 35 900 km (samma som geosynkrona) över jordens ekvator och de fortsätter att rotera i förhållande till jordens riktning (väst till öst). Dessa satelliter anses vara stationära i förhållande till jorden och därav namnet.
Geo-Stationary Earth Orbit Satelliter används för väderprognoser, satellit-TV, satellitradio och andra typer av globala kommunikationer.
Följande figur visar skillnaden mellan geosynkrona och geostationära banor. Rotationsaxeln anger jordens rörelse.
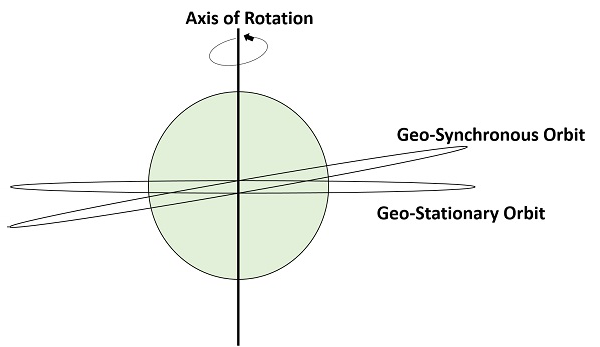
Note – Varje geostationär bana är en geosynkron bana. Men varje geosynkron bana är INTE en geostationär bana.
Medium Earth Orbit Satellites
Medium Earth Orbit (MEO)-satellitnätverk kommer att kretsa på ett avstånd av cirka 8000 mil från jordens yta. Signaler som sänds från en MEO-satellit färdas över en kortare sträcka. Detta innebär en bättre signalstyrka i den mottagande änden. Detta visar att mindre och lättare mottagningsterminaler kan användas i mottagarsidan.
Då signalen färdas en kortare sträcka till och från satelliten blir överföringsfördröjningen mindre. Överföringsfördröjning kan definieras som den tid det tar för en signal att resa upp till en satellit och tillbaka ner till en mottagarstation.
För realtidskommunikation gäller att ju kortare överföringsfördröjning, desto bättre blir kommunikationssystemet. Om en GEO-satellit till exempel behöver 0,25 sekunder för en rundresa, behöver en MEO-satellit mindre än 0,1 sekunder för att genomföra samma resa. MEO-satelliter arbetar i frekvensområdet 2 GHz och högre.
Satelliter i låg omloppsbana
Satelliterna i låg omloppsbana (Low Earth Orbit, LEO) klassificeras huvudsakligen i tre kategorier, nämligen små LEO-satelliter, stora LEO-satelliter och Mega-LEO-satelliter. LEO-satelliterna kommer att kretsa på ett avstånd av 500 till 1000 mil över jordytan.
Detta relativt korta avstånd minskar överföringsfördröjningen till endast 0,05 sekunder. Detta minskar ytterligare behovet av känslig och skrymmande mottagarutrustning. Little LEOs kommer att arbeta i 800 MHz-området (0,8 GHz). Big LEOs kommer att arbeta i området 2 GHz eller högre, och Mega-LEOs arbetar i området 20-30 GHz.
De högre frekvenser som är förknippade med Mega-LEOs innebär en större informationskapacitet och ger möjlighet till videoöverföring i realtid med låg fördröjning.
Följande figur visar vägarna för LEO, MEO och GEO.