
The Policy Question: Skatteavdrag för inköp av hybridbilar – är det regeringens bästa val för att minska bränsleförbrukningen och koldioxidutsläppen?
USA:s invånare och regeringen är oroade över beroendet av importerad utländsk olja och utsläppen av koldioxid i atmosfären. År 2005 antog kongressen en lag för att ge konsumenterna skattelättnader för inköp av el- och hybridbilar.
Denna skattelättnad kan tyckas vara ett bra politiskt val, men den är kostsam eftersom den direkt sänker de intäkter som den amerikanska regeringen samlar in. Finns det effektivare metoder för att minska beroendet av fossila bränslen och koldioxidutsläppen? Hur bestämmer vi vilken politik som är bäst? För att besvara denna fråga måste beslutsfattarna förutsäga med viss exakthet hur konsumenterna kommer att reagera på denna skattepolitik innan dessa beslutsfattare spenderar miljontals federala dollar.
Vi kan tillämpa nyttobegreppet på denna politiska fråga. I den här modulen kommer vi att studera nytta och nyttofunktioner. Vi kommer sedan att kunna använda en lämplig nyttofunktion för att härleda indifferenskurvor som beskriver vår politiska fråga.
Utforskning av den politiska frågan
Antag att skattelättnaden för att subventionera köp av hybridbilar blir en stor framgång och fördubblar den genomsnittliga bränsleekonomin för alla bilar på USA:s vägar – ett resultat som uppenbarligen inte är realistiskt, men som är användbart för våra senare diskussioner. Vad tror du skulle hända med bränsleförbrukningen för alla amerikanska bilister? Bör regeringen förvänta sig att bränsleförbrukningen och koldioxidutsläppen från bilar minskar med hälften som svar på detta? Varför eller varför inte?
2.1 Nyttofunktioner
LO 2.1: Beskriv en nyttofunktion.
2.2 Nyttofunktioner och typiska preferenser
LO 2.2: Identifiera nyttofunktioner utifrån de typiska preferenser de representerar.
2.3 Relatera nyttofunktioner och kartor med indifferenskurvor
LO 2.3: Förklara hur man kan härleda en indifferenskurva från en nyttofunktion.
2.4 Hitta marginalnytta och marginell substitutionsgrad
LO 2.4: Härled marginalnytta och MRS för typiska nyttofunktioner.
2.5. Policy Question
2.1 Nyttofunktioner
LO1: Beskriv en nyttofunktion.
Våra preferenser gör det möjligt för oss att göra jämförelser mellan olika konsumtionspaket och välja de föredragna paketen. Vi skulle till exempel kunna bestämma rangordningen av en hel uppsättning paket utifrån våra preferenser. En nyttofunktion är en matematisk funktion som rangordnar buntar av konsumtionsvaror genom att tilldela varje bunt ett tal där större tal anger föredragna buntar. Nyttofunktioner har de egenskaper som vi identifierade i modul 1 när det gäller preferenser. Det vill säga: de kan ordna buntar, de är kompletta och transitiva, mer är att föredra framför mindre och i relevanta fall är blandade buntar bättre.
Talet som nyttofunktionen tilldelar en specifik bunt är känt som nyttan, den tillfredsställelse som en konsument får av en specifik bunt. Nyttotalet för varje bunt betyder ingenting i absoluta termer; det finns ingen enhetlig skala mot vilken vi mäter tillfredsställelse. Det enda syftet är i relativa termer: vi kan använda nyttan för att avgöra vilka paket som är att föredra framför andra.
Om nyttan från paket A är högre än nyttan från paket B är det likvärdigt med att säga att en konsument föredrar paket A framför paket B. Nyttofunktioner rangordnar därför konsumenternas preferenser genom att tilldela ett nummer till varje paket. . Vi kan använda en nyttofunktion för att rita kartorna med indifferenskurvor som beskrivs i modul 1. Eftersom alla paket på samma indifferenskurva ger samma tillfredsställelse, och inget av dem därför är att föredra, har varje paket samma nytta. Vi kan därför rita en indifferenskurva genom att bestämma alla buntar som ger samma siffra från nyttofunktionen.
Ekonomer säger att nyttofunktioner är ordinala snarare än kardinala. Ordinal innebär att nyttofunktioner endast rangordnar buntar – de anger endast vilken bunt som är bäst, inte hur mycket bättre den är än en annan bunt. Anta till exempel att en nyttofunktion anger att paket A ger 10 nyttigheter och paket B 20 nyttigheter. Vi säger inte att paket B är dubbelt så bra eller 10 nyttigheter bättre, utan bara att konsumenten föredrar paket B. Anta att en vän till exempel deltar i ett lopp och berättar att hon kom på tredje plats. Denna information är ordinal: Du vet att hon var snabbare än fjärdeplaceringen och långsammare än andraplaceringen. Du vet bara i vilken ordning löparna kom i mål. De individuella tiderna är kardinala: Om den som kom först i mål sprang loppet på exakt en timme och din vän kom i mål på en timme och sex minuter vet du att din vän var exakt 10 % långsammare än den snabbaste löparen. eftersom nyttofunktioner är ordinala kan många olika nyttofunktioner representera samma preferenser. Detta gäller så länge ordningsföljden bibehålls.
Tag till exempel nyttofunktionen U som beskriver preferenser för varubundlar A och B: U(A,B). Vi kan tillämpa vilken positiv monoton omvandling som helst på denna funktion (vilket i huvudsak innebär att vi inte ändrar ordningsföljden) och den nya funktion vi har skapat kommer att representera samma preferenser. Vi kan till exempel multiplicera en positiv konstant, α , eller lägga till en positiv eller negativ konstant, β . Så αU(A,B)+β representerar exakt samma preferenser som U(A,B) eftersom den kommer att ordna buntarna på exakt samma sätt. Detta faktum är ganska användbart eftersom det ibland blir lättare att lösa problem om man tillämpar en positiv monoton omvandling av en nyttofunktion.
2.2 Nyttofunktioner och typiska preferenser
LO2: Identifiera nyttofunktioner utifrån de typiska preferenser som de representerar
Det kan handla om buntar av äpplen, A, och bananer, B. En nyttofunktion som beskriver Isaks preferenser för buntar av äpplen och bananer är funktionen U(A,B). Men vilka är Isaks särskilda preferenser för buntar av äpplen och bananer? Anta att Isak har ganska vanliga preferenser för äpplen och bananer som leder till våra typiska indifferenskurvor: Han föredrar mer framför mindre, och han gillar variation. En nyttofunktion som representerar dessa preferenser kan vara:
U(A,B) = AB
Om äpplen och bananer är perfekta komplement i Isaks preferenser skulle nyttofunktionen se ut ungefär så här:
U(A,B) = MIN,
där MIN-funktionen helt enkelt tilldelar det minsta av de två talen som funktionens värde.
Om äpplen och bananer är perfekta substitut är nyttofunktionen additiv och skulle se ut ungefär så här:
U(A,B) = A + B
En klass av nyttofunktioner som kallas Cobb-Douglas-nyttofunktioner är mycket vanligt förekommande inom ekonomin av två skäl:
1. De representerar ”välskötta” preferenser, t.ex. att mer är bättre och att man föredrar variation.
2. De är mycket flexibla och kan mycket lätt anpassas för att passa till data från den verkliga världen.
Cobb-Douglas nyttofunktioner har denna form:
U(A,B) = AαBβ
Då positiva monotona omvandlingar representerar samma preferenser kan en sådan omvandling användas för att ställa in α + β = 1 , vilket vi senare kommer att se är ett bekvämt villkor som förenklar en del matematik i konsumentvalsproblemet.
Ett annat sätt att omvandla nyttofunktionen på ett användbart sätt är att ta den naturliga loggen av funktionen, vilket skapar en ny funktion som ser ut så här:
U(A,B) = αln(A) + βln(B)
För att härleda denna ekvation tillämpar du helt enkelt reglerna för naturliga loggar. . Det är viktigt att komma ihåg abstraktionsnivån här. Vi kan vanligtvis inte göra specifika nyttofunktioner som exakt beskriver individuella preferenser. Förmodligen skulle ingen av oss kunna beskriva våra egna preferenser med en enda ekvation. Men så länge konsumenterna i allmänhet har preferenser som följer våra grundläggande antaganden kan vi göra ett ganska bra jobb med att hitta nyttofunktioner som matchar verkliga konsumtionsdata. Vi kommer att se bevis för detta senare i kursen.
Tabell 2.1 sammanfattar de preferenser och nyttofunktioner som beskrivs i det här avsnittet.
|
Tabell 2.1 Typer av preferenser och de nyttofunktioner som representerar dem |
||
|
PREFERENSER |
NÖJTFunktioner. FUNKTION |
Typ av funktion |
|
Kärlek till variation eller ”välmående” |
U(A,B) = AB |
Cobb-Douglas |
|
Love of Variety or ”Well Behaved” |
U(A,B) = AαBβ |
Cobb-Douglas |
|
Love of Variety or ”Well Behaved” |
U(A,B) = αln(A) + βln(B) |
Naturlig log Cobb-Douglas |
|
Fullkomliga komplement |
U(A,B) = MIN |
Min funktion |
|
Perfekta substitut |
U(A,B) = A + B |
Additiv |
2.3 Relatering av nyttofunktioner och kartor med indifferenskurvor
LO3: Förklara hur man kan härleda en indifferenskurva från en nyttofunktion
Indifferenskurvor och nyttofunktioner är direkt relaterade. Eftersom indifferenskurvor representerar preferenser grafiskt och nyttofunktioner representerar preferenser matematiskt följer det faktiskt att indifferenskurvor kan härledas från nyttofunktioner.
I univariata funktioner plottas den beroende variabeln på den vertikala axeln och den oberoende variabeln på den horisontella axeln, som grafen för y=f(x). Däremot är graferna för bi-variata funktioner tredimensionella, som U=U(A,B). Figur 2.1 visar en graf för U=A^\frac{1}{2}B^\frac{1}{2}. Tredimensionella grafer är användbara för att förstå hur nyttan ökar med ökad konsumtion av både A och B.
Figur 2.1 U=A^\frac{1}{2}B^\frac{1}{2}
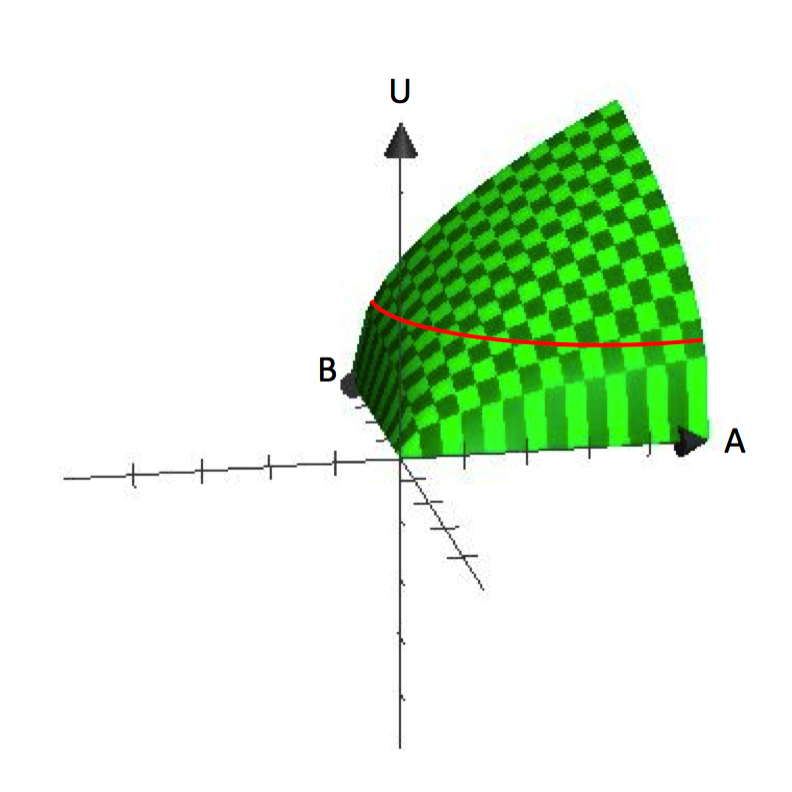
Figur 2.1 visar tydligt antagandet att konsumenterna har en preferens för variation. Varje bunt som innehåller en viss mängd av A och B representerar en punkt på ytan. Ytans vertikala höjd representerar nyttonivån. Genom att öka både A och B kan en konsument nå högre punkter på ytan.
Varifrån kommer då indifferenskurvor? Minns att en indifferenskurva är en samling av alla paket som en konsument är likgiltig inför, med avseende på vilket paket han eller hon ska konsumera. Matematiskt sett är detta likvärdigt med att säga att alla buntar, när de sätts in i nyttofunktionen, ger samma funktionella värde. Om vi fastställer ett värde för nyttan, Ū, och hittar alla kombinationer av A och B som ger detta värde, kommer vi att definiera en indifferenskurva. Observera att detta är likvärdigt med att hitta alla buntar som får konsumenten till samma höjd på den tredimensionella ytan i figur 2.1.
Indifferenskurvor är en representation av höjden (nyttonivån) på en plan yta. På så sätt är de analoga med en höjdkurva på en topografisk karta. Genom att föra tillbaka den tredimensionella grafen till det tvådimensionella rummet – A, B-rummet – kan vi visa de konturlinjer/indifferenskurvor som representerar olika höjder eller nyttonivåer. Från grafen i figur 2.1 kan man redan se hur denna nyttofunktion ger indifferenskurvor som är ”böjda” eller konkava mot ursprunget.
Indifferenskurvor följer alltså direkt av nyttofunktioner och är ett användbart sätt att representera nyttofunktioner i en tvådimensionell graf.
2.4 Hitta marginalnytta och marginell substitutionsgrad
LO4: Härled marginalnytta och MRS för typiska nyttofunktioner.
Marginalnytta är den extra nytta som en konsument får genom att konsumera ytterligare en enhet av en vara. Matematiskt uttrycker vi detta som:
MU_{a}=\frac{\Delta \cup }{\Delta A}
eller förändringen av nyttan från en förändring av mängden A som konsumeras, där Δ representerar en förändring av varans värde. Så,
MU_{a}=\frac{\Delta \cup }{\Delta A}=\frac{\cup (A+\Delta A,B)-U(A,B)}{\Delta A}
Bemärk att när vi undersöker marginalnyttan av konsumtionen av A, håller vi B konstant.
Med hjälp av kalkyl är marginalnyttan detsamma som den partiella derivatan av nyttofunktionen med avseende på A:
MU_{A}\frac{\partial U(A,B)}{\partial A}
Tänk på en konsument som sätter sig ner för att äta en måltid med sallad och pizza. Anta att vi håller mängden sallad konstant – en sallad till en middag, till exempel. Låt oss nu öka antalet pizzasnittar antar att med 1snitt är nyttan 10, med 2 är den 18, med 3 är den 24 och med 4 är den 28. Låt oss plotta dessa siffror på en graf som har nyttan på den vertikala axeln och pizzan på den horisontella axeln (figur 2.2).
Figur 2.2: Graf och tabell över avtagande marginalnytta
|
Pizzabitar |
Nytta |
Marginalnytta |
. Utility |
|
1 |
10 |
|
|
|
2 |
18 |
8 |
|
|
3 |
24 |
6 |
|
|
4 |
28 |
4 |
|
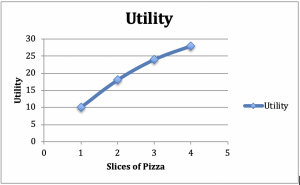
Från den positiva lutningen på grafen, kan vi se den ökade nyttan av ytterligare pizzabitar. Från den konkava formen på grafen kan vi se ett annat vanligt fenomen: Den extra nytta som konsumenten får från varje extra pizzabit minskar med antalet pizzabitar som konsumeras.
Det faktum att den extra nyttan blir mindre med varje extra pizzabit kallas för principen om minskande marginalnytta. Denna princip gäller för välfungerande preferenser där blandade paket är att föredra.
Marginal substitution Rate of Substitution (MRS) är den mängd av en vara som en konsument är villig att ge upp för att få ytterligare en enhet av en annan vara. Det är därför det är samma sak som lutningen på indifferenskurvan – eftersom vi håller tillfredsställelsenivån konstant förblir vi på samma indifferenskurva, vi rör oss bara längs den när vi byter en vara mot en annan. Hur mycket av den ena du är villig att byta för en mer av den andra beror på den marginella nyttan av var och en.
Om vi använder vårt tidigare exempel, om du genom att konsumera ytterligare en sidosallad ökar din nytta med 10, kan du vid en nuvarande konsumtion av 4 pizzasnittar ge upp 2 pizzasnittar och gå från 28 till 18 nyttor. 10 mer nyttor från salladen och 10 mindre nyttor genom att ge upp 2 pizzabitar gör att den totala nyttan förblir oförändrad – så vi måste fortfarande befinna oss på samma indifferenskurva. När du rör dig längs indifferenskurvan måste du rida på lutningen, det vill säga du måste ge upp varan på den vertikala axeln för mer av varan på den horisontella axeln, vilket ger en negativ uppgång över en positiv uppgång.
Vi kan gå direkt från marginalnytta till MRS genom att inse sambandet mellan de två begreppen. I vårt fall, för en nyttofunktion U=U(A,B) , representeras MRS som:
MRS=-\frac{MU_{A}}{MU_{B}}
Bemärk att när vi ersätter kan vi förenkla ekvationen:
MRS=-\frac{MU_{A}}{MU_{B}}=-\frac{\frac{\Delta U}{\Delta A}}{\frac{\Delta U}{\Delta B}}=-\frac{\Delta B}{\Delta A}
Inför beräkningen motsvarar det:
MRS=-\frac{\frac{\frac{\partial U(A,B)}{\partial A}}{\frac{\partial U(A,B)}{\partial B}}
2.5 Politisk fråga
Vi fastställde i modul 1 att det relevanta konsumentbeslutet mellan fler körda mil och annan konsumtion förmodligen överensstämmer med standardantagandena om konsumentval. Därför är det ett bra val att använda Cobb-Douglas nyttofunktion för att representera en konsument som både gillar att köra bil och att konsumera andra varor, och som ser dem som en avvägning (pengar som spenderas på bensin är pengar som inte spenderas på andra konsumtionsvaror). Den har också fördelarna av att både överensstämma med antagandena och vara flexibel:
U(MD,C)=MD^{a}C^{\beta } ,
där MD = körda mil och C = annan konsumtion.
Funktionen i sig kan faktiskt användas för verkliga data där parametrarna och kan uppskattas för denna marknad, marknaden för körda mil i konsumentens bil.
Figur 2.3 Diagram över indifferenskurvor för det politiska exemplet
Undersökning av de politiska frågorna:
1 . Skulle andra preferenstyper vara mer lämpliga i det här exemplet?
2. Vad måste vara sant för att perfekta komplement ska vara den lämpliga preferenstypen att använda för att analysera den här politiken?
Vad måste vara sant för perfekta substitut? Med tanke på att vi betraktar en ”typisk” konsument som kör bil, är det lämpligt att välja en ”typisk” nyttofunktion?
4. Är det bara en gissning eller har vi någon teoretisk grund för att stödja vårt val av ”välskötta” preferenser eller en Cobb-Douglas-nyttofunktion?
SAMMANFATTNING
Översyn: Ämnen och relaterade lärandemål
2.1 Nyttofunktioner
LO 2.1: Beskriv en nyttofunktion
2.2 Nyttofunktioner och typiska preferenser
LO 2.2: Identifiera nyttofunktioner utifrån de typiska preferenser de representerar
2.3 Relatera nyttofunktioner och kartor med indifferenskurvor
LO 2.3: Förklara hur man kan härleda en indifferenskurva från en nyttofunktion
2.4 Hitta marginalnytta och marginell substitutionsgrad
LO 2.4: Härled marginalnytta och MRS för typiska nyttofunktioner
2.5. Policy Question
Lär dig: Nyckeltermer och grafer
Bi-variata funktioner
Kardinalfunktion
Konturlinje
Minskande marginalnytta
Funktion
Marginell substitutionsgrad (MRS)
Marginalnytta
Ordinell
Univariella funktioner
Util
Nytta
Nyttafunktion
Grafer
3D-nyttafunktion och konturlinje
Svårdsräkningar
Cobb-Douglas
Perfekta komplement
Perfekta substitut