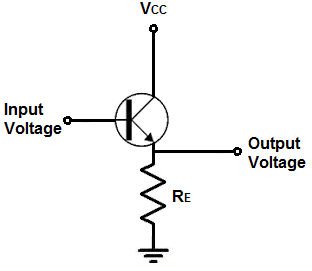
I det här projektet kommer vi att visa hur man bygger en buffert med en transistor. med några resistorer och kondensatorer.
En buffert är en anordning som ger ut samma spänning som matas in i den.Den kan tjäna en myriad av användningsområden, till exempel tillåta maximal spänningsöverföring och orsaka låg strömbelastning från en strömförsörjning.
Denna krets använder inte en integrerad krets som en IC-buffert.
Den använder endast enkla komponenter.
Den typ av transistor som vi använder är en bipolär junctiontransistor av NPN-typ. vilken som helst kan användas; populära är 2N3904 och 2N2222.
Transistorkretsen kommer att konfigureras som en emitterföljare (ett annat namn ärcommon collector circuit).
En emitterföljarkrets är en transistorkrets där spänningen vid emittern följer ingångsspänningen. Den är så att säga en spegelbild av ingångsspänningen. Därför är spänningen vid utgången densamma som spänningen vid ingången.
Då utgångsspänningen är en spegelbild av ingångsspänningen och ingångsimpedansen är stor och utgångsimpedansen är liten fungerar emitterföljaren som en buffert.
Om en spänningsledning behöver buffras kan den därför anslutas till ingången i denna krets och belastningen som behöver strömförsörjas ansluts till utgången i denna krets.
Detta är bra när man inte har ett buffertchip tillgängligt eller ett logikchip som man kan omvandla till en buffert.
I vår krets, specifikt, kommer ingångsimpedansen att vara över 50KΩ och utgångsimpedansen kommer att vara ungefär 5Ω. Detta är skapar en ganska bra buffertverkan på alla spänningar som behöver buffras.
Vi kommer att konstruera denna typ av transistorkrets för att fungera som en buffert.
För att korrekt konstruera en emitterföljarkrets måste flera faktorer beaktas, bland annat hur mycket likspänning som tillförs transistorens kollektor, hur mycket ström som önskas passera genom transistorn och frekvenskopplingen av de växelströmssignaler som kommer in i ingången.
Vi kommer att gå igenom alla dessa begrepp mycket ingående nedan. Vi kommer i den här kretsen att visa hur man konfigurerar den och hur man väljer värdena på motstånden och kondensatorerna, vilket kallas transistorbiasing.
Komponenter som behövs
- 2N3904 NPN-transistor
- 1KΩ motstånd
- 1.1KΩ motstånd
- 500Ω motstånd
- 16μF elektrolytkondensator
- 1600μF elektrolytkondensator
Transistorn som väljs kan egentligen vara vilken BJT NPN transistor som helst. För den här kretsen väljer vi transistorn 2N3904.
För många av värdena för de komponenter som vi faktiskt beräknar kommer du inte att kunna hitta dessa exakta värden. Nedan beräknar vi till exempel ett av motstånden till 565Ω. Detta motstånd existerar inte. Så vi gör en uppskattning. Det är möjligt att hitta ett motstånd på 500Ω och även om du inte kan det kan du sätta 2 motstånd på 1 KΩ parallellt för att få ett ekvivalent motstånd på 500Ω.
Ett motstånd på 1,1 KΩ hittar du inte heller. Så du kan antingen approximera ner till 1KΩ eller sätta ett 1KΩ-motstånd i serie med ett 100Ω-motstånd. För alla grundläggande ändamål är detta inte nödvändigt. Du kan helt enkelt ansluta ett 1KΩ-motstånd i stället för 1,1KΩ. Det ger liknande resultat.
Samma approximationer bör användas för kondensatorvärdena. Hitta ett värde som ligger så nära de beräknade kondensatorvärdena som möjligt och använd dessa.
Transistorbufferkrets
Bufferkretsen som vi ska bygga med en enda NPN BJT-transistoroch några motstånd och kondensatorer visas nedan.
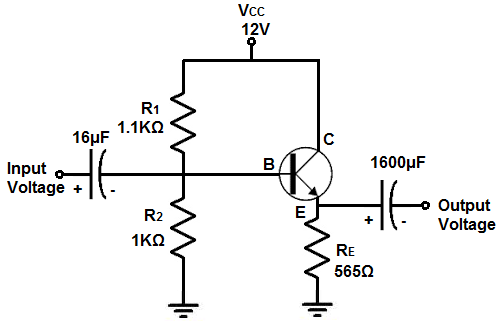
Brödbrädapparatskretsen av kretsen ovan visas nedan. 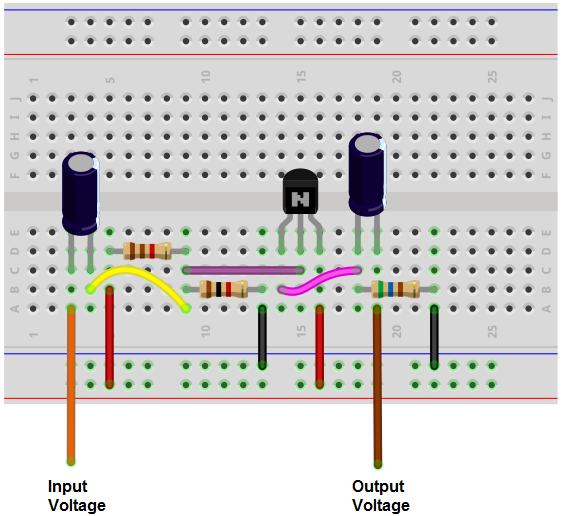
Så kretsen ovan fungerar som en buffert. Den ledning som du vill buffra ansluts till ingången och den belastning som du vill ha påslagen ansluts till kretsens utgång.
Vi kommer nu att gå in på detaljerna om varför de olika komponenterna behövs för kretsen och hur man väljer värden för dem.
Det första är alltså att vi bestämmer hur mycket spänning vi ska tillföra kretsen. Detta är den spänning, VCC, som läggs på transistorens kollektor. Du kan egentligen välja vilket värde som helst från över VB, basspänningen, till det maximala värdet som transistorn klarar av på kollektorn. Detta är vanligtvis 40-60 V på de flesta transistorer. För vår krets kommer vi att välja ett rimligt spänningsvärde på 12 för VCC, så detta är det första övervägandet.
Nästan, nu när vi känner till VCC, biasar vi kretsens basspänning, vilket innebär att vi väljer den spänning som vi vill ska falla över transistorens bas. vilket värde vill vi ha över basen? För att svara på detta tittar vi på hela bilden. Mängden växelspänning som kan finnas vid transistorens utgång är beroende av det likspänningsområde som kretsen har. I ena änden av spektrumet kan transistorn svänga upp till 12V, vilket är VCC. I den andra änden av spektrumet kan transistorn svänga ner till nära jord, ca 0,7 V. Anledningen till att transistorn inte kan svänga helt till jord är att transistorn inte kommer att slå på om inte dioden slås på och det sker vid ungefär 0,7V, barriärspänningen för den interna dioden. Därför är 0,7V kretsens golv och inte jord eller 0V. Med en strömförsörjning på 12 V och en jord 0,7 V kan transistorn därför svänga från 0,7 V upp till 12 V. Varför detta har betydelse för den spänning som vi levererar till basen är att oavsett vilken spänning som kommer in i kretsen har den ett golv på 0,7V och ett tak på 12V. Därför vill vi förspänna basspänningen så att den faller mellan dessa värden. Detta ger en maximal topp-till-topp-utslag för signalen och ger den mest utrymme för att fungera utan att klippa. Om basspänningen är felaktigt polariserad eller ligger långt från mitten, kan transistorn få betydande clipping som ger dålig utgångseffekt. För ett tak på 12 V och ett golv på 0,7 V skulle medelvärdet vara (12 – 0,7 V)/2 +0,7 V= 6,35 V. Vi måste ta hänsyn till diodspänningsfallet eftersom värdet vid basen är 0,7V högre än vid utgången. Genom att förspänna basspänningen mitt i mitten av taket och golvet möjliggörs maximal svängning av växelströmssignalen, så kallad maximal peak-to-peak-exkursion. När man polariserar en transistorkrets som hanterar växelströmssignaler, motsvarar den växelströmssignal som kommer att kunna förekomma vid utgången utan att klippet begränsasDC-biasering. Växelströmssignalen kan bara svänga så långt som likspänningen tillåter den. Om spänningen är 20 V och golvet är 0,7 V kan transistorn svänga från ett toppvärde på 20 V till ett golv på 0,7 V. Genom att placera transistorn i mitten av dessa spänningar kan växelströmssignalen svänga maximalt från taket till golvet. Detta är den optimala DC-driftspunkten för kretsen, kallad Q-punkten eller vilopunkten.Om du väljer ett DC-värde som är för lågt kommer du att få signalen att klippa tidigare i botten av vågformen. Om du väljer en för hög likströmsdriftsspänning kommer du att få signalen att klippa i toppen av vågformen.
Så baserat på denna punkt vill vi att spänningen vid basen ska ligga mitt emellan 12V, matningsspänningen, och 0,7V, som representerar golvet. Så att VB= 0,7V + (12V-0,7V)/2, vilket är 6,35V. Så för att få denna spänning måste vi välja våra motstånd så att denna spänning kan uppstå vid basen. Spänningen vid basen är förspänd genom två motstånd. Motstånden bildar en spänningsdelare och delar upp matningsspänningen. Vi kan dela vår matningsspänning till vilken spänning som helst som är lägre än matningsspänningen genom att välja rätt värde på motstånden. Basspänningen VB= VCC * (R2/R1+R2). För att lösa denna ekvation väljer vi värdet på ett motstånd och beräknar sedan värdet på det andra motståndet utifrån denna formel. För motståndet R2 väljs alltså ett värde på 1 KΩ som referenspunkt för det andra motståndet. Genom att sätta in dessa värden i formeln får viVB= VCC * (R2/R1+R2)= 6,35V (12V) (1KΩ). /(R1+1KΩ). Om man räknar på detta, ger det ett värde på R1= 1,1 KΩ. Så för att få ett värde på 6,35V vid basen är motstånden R1 lika med 1,1KΩ och R2=1KΩ.
Nästan måste vi bestämma värdet på motståndet RE. Värdet som vi väljer är integrerat så att vi inte överhettar och eventuellt förstör transistorn. Hur vi väljer RE baseras på värdet på strömmen, IE som vi vill följa genom transistorn och vad som är en säker ström att flöda genom transistorn. Så vi väljer bara ett intervall som är en säker ström som kan flöda genom transistorn och som inte bränner ut den. En säker ström är 10 mA. Det är en anständig mängd ström och en som inte kommer att bränna ut transistorn. Emittermotståndet, RE= VE/IE, där VE är spänningen över emittern och IE är strömmen som flyter genom emittern. VE=VB-0,7V = 5,65V. Den enda skillnaden i spänning mellan basspänningen och emitterspänningen är diodspänningsfallet mellan de två förbindningarna. Eftersom transistorn har en diod i sig från basen till emittern har transistorn ett internt spänningsfall. Därför är emitterspänningen lika med basspänningen minus spänningsfallet över dioden. Formeln RE= VE/IE= 5,65V/10mA= 565Ω. Så ett RE-motstånd på cirka 500Ω skulle räcka bra för den här kretsen.
Nu sist måste vi välja värdet på kondensatorerna i den här kretsen. Båda kondensatorerna har samma funktion. De tillåter endast växelströmssignalen att passera och blockerar likströmmen från att passera. De fungerar alltså som kopplingskondensatorer.
Vi ska först visa hur man beräknar värdet på kondensatorn vid ingången.
För att korrekt välja ett lämpligt värde på kondensatorn måste vi ta hänsyn till många saker, som vi nu ska diskutera.
En, vi måste bestämma kretsens gränsfrekvens. Detta är den frekvens som vi vill filtrera bort. Om du har att göra med ljudsignaler är det frekvensområde som är hörbart för människor 20 Hz till 20 000 Hz. Om du bygger vår transistor så att vi bara vill att hörbara signaler ska passera igenom är 20 Hz en bra gränsfrekvens att välja. Detta innebär att alla frekvenser i det intervallet eller lägre kommer att filtreras ut till jord. Så vi kommer att välja 20 Hz som vår avgränsningsfrekvens. Om vi tar 20 Hz och tillämpar det på vinkelfrekvensen, ω=2πf, får vi ω=2πf≈125s-1. Detta är en del av ekvationen.
Nästa sak vi måste ta hänsyn till är värdet på det motstånd som kondensatorn ser. Den första delen av denna krets från kondensatorn och motståndet som den ser ner till jord bildar ett högpassfilter, ett RC-högpassfilter. Ett RC-högpassfilter är en krets som består av en kondensator med ett motstånd kopplat till jord.
Om du visualiserade strömmen som flödar in i kretsen kan strömmen gå antingen 1 av 3 vägar. Strömmen kan gå genom kondensatorn och genom motståndet R2 och ner till jord. Strömmen kan gå genom kondensatorn och genom motståndet R1. Eller så kan strömmen röra sig genom transistorn och röra sig genom motståndet RE ner till jord. Det kan tyckas märkligt att strömmen kan flöda genom R1-resistorn, men växelströmssignaler ser likspänningsnivåer som jord också. Så även om det är en likströmsnivå på 12 V (genom R1) kan det för växelströmssignaler också vara en jord, vilket är anledningen till att detta också kan vara en väg ner till jord.
Dessa är alltså de 3 sätt som strömmen kan flöda i kretsen. Även om strömmen kan ta dessa vägar är det i slutändan vad en kondensator ser som bestämmer det verkliga motståndet som den möter. Så vi ska prata om detta nu. Resistorerna R1och R2 är parallella. Därför ser kondensatorn det ekvivalenta motståndet för dessa två parallella motstånd. Kondensatorn ser alltså 1 KΩ parallellt med motståndet 1,1 KΩ. Det ekvivalenta motståndet för dessa motstånd är ungefär 500Ω. Så detta är det motstånd som kondensatorn ser vid en väg. Den andra vägen är när strömmen går genom transistorn och genom motstånd RE. Detta motstånd blir βRE. Med β lika med ungefär 100, om man gör denna matematik, beräknas detta motstånd till56KΩ.
Håll dig i minnet att strömmen alltid tar den väg som ger minst motstånd. Så mellan alternativen 500Ω eller 56KΩ kommer strömmen uppenbarligen att ta vägen med 500Ω.
Så 500Ω är det ekvivalenta motstånd som RC-högpassfilternätverket ser och vi vet att vi vill ha en gränsfrekvens på 20 Hz. Och genom att beräkna vinkelfrekvensen för 20 Hz får vi ω=2πf≈125s-1.
Så om vi går till ekvationen, REQC1= 1/125s-1= (500Ω)C1= 0,008s. Om man räknar på det, ger det ett C1-värde på 16µF. Så den första kondensatorn är 16µF.
Nu går vi vidare till den andra kondensatorn. Och den väljs på samma sätt som den första kondensatorn.
Vi vill att den andra kondensatorn skall reagera på samma sätt som den första, när det gäller den frekvens som vi har att göra med. Detta beror på att samma frekvenssignal som går in också går ut. Så du vill matcha frekvensresponsen för båda kondensatorerna. Så för utgångskondensatorn beräknar vi också den enligt dess frekvensrespons på 20 Hz. Genom att beräkna vinkelfrekvensen får vi återigen ω=2πf≈125s-1.
Vi använder samma formel igen, REQC2= 1/125s-1.
Vad är REQ i det här fallet? REQ är det motstånd som utgångskondensatorn ser i kretsen. Om vi tittar från kondensatorn tillbaka till ingångssidan ser kondensatorn ett motstånd på (R1 || R2)/β= (1,1KΩ || 1KΩ)/100= (523Ω/100) ≈ 5Ω. Så utgångskondensatorn ser ett ekvivalent motstånd på 5Ω när den tittar tillbaka till kretsens ingång.
Så genom att sätta in dessa värden i ekvationen får man REQC2= 1/125s-1= (5Ω)C2= 0,008s. Genom att lösa C2 får vi 1600µF. Detta är alltså värdet på utgångskondensatorn.
Och nu har vi löst alla värden för komponenterna i kretsen.
Du kan se utifrån beräkningarna att kretsen har en hög ingångsimpedans och en låg utgångsimpedans. Som vi beräknade är ingångsimpedansen βRE, som vi beräknade till 56KΩ. Utgångsimpedansen beräknade vi till 5Ω. Så du kan se hur den här kretsen har hög ingångsimpedans och låg utgångsimpedans.
Så den fungerar mycket bra som buffert.
Den här kretsen kan läggas till på en spänningsledning som behöver buffras, vilket gör att all spänning kan föras över, samtidigt som den ger en utgång med låg impedans så att en belastning kan strömförsörjas.
Vet att det här är en grundläggande buffertkrets. Den är inte lika exakt som ett riktigt buffertchip. För det första har ett buffertchip större impedans och lägre utgångsimpedans. För det andra är det inte en helt korrekt spänningsföljarkrets. Eftersom transistorn har en intern diod som har ett spänningsfall som ungefär motsvarar 0.7V, förlorar den denna spänning vid utgången. Utgångssignalen är alltså 0,7 V lägre än ingångssignalen. Så du kan se att det inte helt och hållet är en spänningsföljare.
För alla grundläggande ändamål fungerar den dock mycket bra som en buffert med låg precision.