I den här lektionen kommer vi att visa en enkel strategi för att lösa följande problem: hur man hittar arean av en likbent triangel.
Låt oss omsätta ett antal av de egenskaper som vi hittills har bevisat i praktiken i följande geometriproblem:
Problem
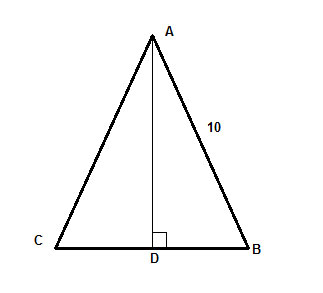
I en likbent triangel, ΔABC, med benlängden 10, är höjden till basen lika med två tredjedelar av basen. Hitta triangelns area.
Strategi
För att lösa detta problem arbetar vi baklänges från vad vi behöver göra.
Vi behöver hitta triangelns area, som vi vet ges av formeln (basen gånger höjden)/2.
Ett problem som vi har är att vi inte vet vare sig basens längd eller höjden. Men vi får förhållandet mellan dem, vilket är en antydan om vad vi måste göra. Låt oss kalla basens längd, BC, för x.
Därefter vet vi att höjden, AD, är 2x/3, vilket anges i problemet.
Så svaret vi letar efter är (basen gånger höjden)/2, eller x gånger 2x/3, dividerat med två.
Men hur hittar vi x? Det finns ytterligare två saker som vi fick i problemet som vi inte har använt ännu – benets längd (10) och det faktum att detta är en likbent triangel. Vi behöver förmodligen använda dessa två saker för att lösa problemet.
Låt oss gå igenom egenskaperna hos likbenta trianglar. En sak som omedelbart borde falla oss in är att som vi har visat, i en likbent triangel är höjden till basen bisektrisk, så CD=DB=x/2.
Slutligen är AD höjden, vilket innebär att vinkeln ∠ADC är en rät vinkel, och vi har en rätvinklig triangel, ΔADC, vars hypotenusa vi känner till (10) och kan använda för att hitta benen med hjälp av Pythagoras sats, c2 =a2+b2,
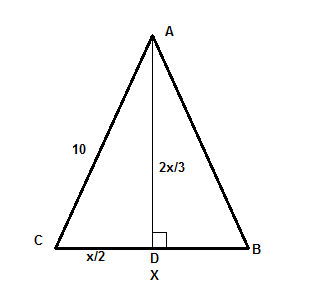
där c= 10 , a = x/2 och b=2x/3 . Och vi är klara, resten är bara algebraisk lösning av x.
Bevis:
(1) ΔADC är en rätvinklig triangel //given, eftersom AD är höjden till basen
(2) AC2 =CD2 + AD2 /Pythagoras sats
(3) AC= 10 //given
(4) CB = x
(5) CD = x/2 /Höjden till basen i den likbenta triangeln halverar basen
(6) AD = 2x/3 //given
(7) 102 = (x/2)2 + (2x/3)2 //Substituera i (2)
(8) 100 = x2/4+4×2/9 /förenkla
(9) 100*36 = 9×2 +16×2 //multiplicera båda sidor med 36
(10) 100*36 = 25×2 //samla liknande termer