Standardavvikelsen är den genomsnittliga mängden variabilitet i ditt dataset. Den talar om hur långt varje värde i genomsnitt ligger från medelvärdet.
En hög standardavvikelse innebär att värdena i allmänhet ligger långt från medelvärdet, medan en låg standardavvikelse indikerar att värdena är grupperade nära medelvärdet.
Vad säger standardavvikelsen om dig?
Standardavvikelsen är ett användbart mått på spridningen för normalfördelningar.
I normalfördelningar är data symmetriskt fördelade utan snedfördelning. De flesta värden grupperar sig runt ett centralt område, med värden som avtar när de kommer längre bort från centrum. Standardavvikelsen talar om hur utspridda dina data i genomsnitt är från fördelningens centrum.
Många vetenskapliga variabler följer normalfördelningar, t.ex. längd, standardiserade testresultat eller betyg på arbetstillfredsställelse. När du har standardavvikelserna för olika urval kan du jämföra deras fördelningar med hjälp av statistiska tester för att dra slutsatser om de större populationer som de kommer från.
Medelbetygen (M) är desamma för varje grupp – det är värdet på x-axeln när kurvan är på sin topp. Deras standardavvikelser (SD) skiljer sig dock från varandra.
Standardavvikelsen återspeglar spridningen i fördelningen. Kurvan med den lägsta standardavvikelsen har en hög topp och en liten spridning, medan kurvan med den högsta standardavvikelsen är mer platt och utbredd.
Den empiriska regeln
Standardavvikelsen och medelvärdet kan tillsammans tala om för dig var de flesta av värdena i din fördelning ligger om de följer en normalfördelning.
Den empiriska regeln, eller 68-95-99,7-regeln, talar om för dig var dina värden ligger:
- Omkring 68 % av poängen ligger inom 2 standardavvikelser från medelvärdet,
- Omkring 95 % av poängen ligger inom 4 standardavvikelser från medelvärdet,
- Omkring 99.7% av poängen ligger inom 6 standardavvikelser från medelvärdet.
Följs den empiriska regeln:
- Omkring 68 % av poängen ligger mellan 40 och 60.
- Omkring 95 % av poängen ligger mellan 30 och 70.
- Omkring 99,7 % av poängen ligger mellan 20 och 80.
Den empiriska regeln är ett snabbt sätt att få en överblick över dina data och kontrollera om det finns några outliers eller extremvärden som inte följer detta mönster.
För icke-normala fördelningar är standardavvikelsen ett mindre tillförlitligt mått på variabilitet och bör användas i kombination med andra mått som intervallet eller interkvartilintervallet.
Standardavvikelseformler för populationer och stickprov
Differentierade formler används för att beräkna standardavvikelser beroende på om du har data från en hel population eller ett stickprov.
Populationens standardavvikelse
När du har samlat in data från varje medlem av den population som du är intresserad av kan du få ett exakt värde för populationens standardavvikelse.
Formeln för populationens standardavvikelse ser ut så här:
| Formel | Förklaring |
|---|---|
 |
|
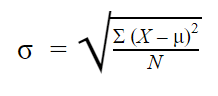Samplingens standardavvikelse
När du samlar in data från ett stickprov används stickprovets standardavvikelse för att göra uppskattningar eller slutsatser om populationens standardavvikelse.
Formeln för urvalets standardavvikelse ser ut så här:
| Formel | Förklaring |
|---|---|
 |
|
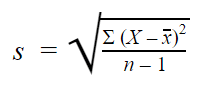Med prover använder vi n – 1 i formeln, eftersom användning av n skulle ge en snedvriden skattning som konsekvent underskattar variabiliteten. Standardavvikelsen i urvalet skulle tendera att vara lägre än den verkliga standardavvikelsen i populationen.
Reducerar man urvalet n till n – 1 blir standardavvikelsen artificiellt stor, vilket ger en konservativ uppskattning av variabiliteten.
Detta är visserligen inte en fördomsfri uppskattning, men det är en mindre fördomsfri uppskattning av standardavvikelsen: det är bättre att överskatta än att underskatta variabiliteten i stickprov.
Steg för att beräkna standardavvikelsen
Standardavvikelsen beräknas vanligtvis automatiskt av den programvara du använder för din statistiska analys. Men du kan också beräkna den för hand för att bättre förstå hur formeln fungerar.
Det finns sex huvudsteg för att hitta standardavvikelsen för hand. Vi kommer att använda ett litet dataset med 6 poäng för att gå igenom stegen.
| Dataset | |||||
|---|---|---|---|---|---|
| 46 | 69 | 32 | 60 | 52 | 41 |
Steg 1: Hitta medelvärdet
För att hitta medelvärdet adderar du alla poäng och dividerar dem sedan med antalet poäng.
x̅ = (46 + 69 + 32 + 60 + 52 + 41) ÷ 6 = 50
Steg 2: Hitta varje poängs avvikelse från medelvärdet
Subtrahera medelvärdet från varje poäng för att få avvikelserna från medelvärdet.
Då x̅ = 50, drar vi här bort 50 från varje poäng.
| Poäng | Avvikelse från medelvärdet |
|---|---|
| 46 | 46 – 50 = -.4 |
| 69 | 69 – 50 = 19 |
| 32 | 32 – 50 = -18 |
| 60 | 60 – 50 = 10 |
| 52 | 52 – 50 = 2 |
| 41 | 41 – 50 = -9 |
Steg 3: Kvadrera varje avvikelse från medelvärdet
Multiplicera varje avvikelse från medelvärdet med sig själv. Detta kommer att resultera i positiva tal.
(-4)2 = 4 × 4 = 16
192 = 19 × 19 = 361
(-18)2 = -18 × -18 = 324
102 = 10 × 10 = 100
22 = 2 × 2 = 4
(-9)2 = -9 × -9 = 81
Steg 4: Hitta summan av kvadraterna
Addera alla kvadrerade avvikelser. Detta kallas summan av kvadraterna.
16 + 361 + 324 + 100 + 4 + 81 = 886
Steg 5: Hitta variansen
Divider summan av kvadraterna med n – 1 (för ett urval) eller N (för en population) – detta är variansen.
Då vi arbetar med ett urval på 6 kommer vi att använda n – 1, där n = 6.
886 ÷ (6 – 1) = 886 ÷ 5 = 177.2
Steg 6: Hitta kvadratroten av variansen
För att hitta standardavvikelsen tar vi kvadratroten av variansen.
√177,2 = 13,31
Från att lära sig att SD = 13.31 kan vi säga att varje poäng avviker från medelvärdet med 13,31 poäng i genomsnitt.
Varför är standardavvikelse ett användbart mått på variabilitet?
Och även om det finns enklare sätt att beräkna variabilitet väger formeln för standardavvikelse ojämnt utspridda prover mer än jämnt utspridda prover. En högre standardavvikelse visar att fördelningen inte bara är mer utspridd, utan också mer ojämnt utspridd.
Detta innebär att den ger dig en bättre uppfattning om variabiliteten i dina data än enklare mått, t.ex. den absoluta medelavvikelsen (MAD).
Den absoluta medelavvikelsen (MAD) liknar standardavvikelsen, men är enklare att beräkna. Först uttrycker du varje avvikelse från medelvärdet i absoluta värden genom att omvandla dem till positiva tal (till exempel blir -3 till 3). Sedan beräknar du medelvärdet av dessa absoluta avvikelser.
Till skillnad från standardavvikelsen behöver du inte beräkna kvadrater eller kvadratrötter av tal för MAD. Men av den anledningen ger den dig ett mindre exakt mått på variabiliteten.
Låt oss ta två prover med samma centrala tendens men olika mycket variabilitet. Prov B är mer variabelt än prov A.
| Värden | Medelvärde | Medelvärde absolut avvikelse | Standardavvikelse | |
|---|---|---|---|---|
| Prov A | 66, 30, 40, 64 | 50 | 15 | 17.8 |
| Prov B | 51, 21, 79, 49 | 50 | 15 | 23,7 |
För prover med lika stora genomsnittliga avvikelser från medelvärdet kan MAD inte skilja mellan olika nivåer av spridning. Standardavvikelsen är mer exakt: den är högre för urvalet med större variation i avvikelser från medelvärdet.
Då standardavvikelsen kvadrerar skillnaderna från medelvärdet återspeglar standardavvikelsen ojämn spridning på ett mer exakt sätt. Detta steg väger extrema avvikelser tyngre än små avvikelser.
Detta gör dock också standardavvikelsen känslig för outliers.
Frekventa frågor om standardavvikelse
Variabilitet mäts oftast med följande beskrivande statistik:
- Intervall: Skillnaden mellan det högsta och lägsta värdet
- Interkvartilområde: Standardavvikelse: genomsnittligt avstånd från medelvärdet
- Varians: genomsnittet av kvadrerade avstånd från medelvärdet
Standardavvikelsen är den genomsnittliga mängden variabilitet i din datamängd. Den talar om för dig hur långt varje värde i genomsnitt ligger från medelvärdet.
I normalfördelningar innebär en hög standardavvikelse att värdena i allmänhet ligger långt från medelvärdet, medan en låg standardavvikelse indikerar att värdena är grupperade nära medelvärdet.
I en normalfördelning är data symmetriskt fördelade utan skevhet. De flesta värden samlas kring ett centralt område, och värdena avtar ju längre bort från centrum de kommer.
Måtten för den centrala tendensen (medelvärde, läge och median) är exakt desamma i en normalfördelning.
Den empiriska regeln, eller 68-95-99,7-regeln, talar om var de flesta värdena ligger i en normalfördelning:
- Omkring 68 % av värdena ligger inom 1 standardavvikelse från medelvärdet.
- Omkring 95 % av värdena ligger inom 2 standardavvikelser från medelvärdet.
- Omkring 99.7 % av värdena ligger inom 3 standardavvikelser från medelvärdet.
Den empiriska regeln är ett snabbt sätt att få en överblick över dina data och kontrollera om det finns outliers eller extrema värden som inte följer detta mönster.
Varians är den genomsnittliga kvadrerade avvikelsen från medelvärdet, medan standardavvikelsen är kvadratroten av detta tal. Båda måtten återspeglar variabiliteten i en fördelning, men deras enheter skiljer sig åt:
- Standardavvikelsen uttrycks i samma enheter som de ursprungliga värdena (t.ex. minuter eller meter).
- Varians uttrycks i mycket större enheter (t.ex. meter i kvadrat).
Även om enheterna för varians är svårare att förstå intuitivt, så är varians viktig i statistiska tester.