I den moderna ljudåldern kan du inte undvika att nämna ”Hi-Res” och 24-bitars ”Studio Quality”-musik. Om du inte har upptäckt trenden i avancerade smartphones – Sonys LDAC Bluetooth codec – och streamingtjänster som Tidal, måste du verkligen börja läsa den här webbplatsen mer.
Löftet är enkelt – överlägsen lyssningskvalitet tack vare mer data, även kallad bitdjup. Det är 24 bitar av digitala ettor och nollor jämfört med den ynka 16-bitars baksmälla från CD-eran. Naturligtvis måste du betala extra för dessa produkter och tjänster av högre kvalitet, men fler bitar är säkert bättre, eller hur?
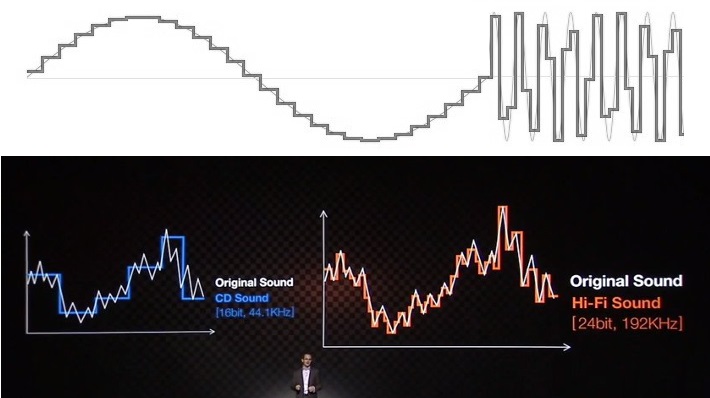
”Lågupplöst” ljud visas ofta upp som en vågform i form av en trappa. Detta är inte hur sampling av ljud fungerar och inte heller hur ljudet ser ut när det kommer ut ur en enhet.
Inte nödvändigtvis. Behovet av högre och högre bitdjup är inte baserat på vetenskaplig verklighet, utan snarare på en förvrängning av sanningen och utnyttjande av konsumenternas bristande medvetenhet om ljudets vetenskap. I slutändan har företag som marknadsför 24-bitars ljud mycket mer att vinna i vinst än vad du har i överlägsen uppspelningskvalitet.
Bitdjup och ljudkvalitet:
För att antyda att 24-bitars ljud är ett måste, drar företagen (och alltför många andra som försöker förklara detta ämne) fram den mycket välkända ljudkvalitetstrappan till himlen. 16-bitarsexemplet visar alltid en ojämn, kuperad återgivning av en sinusvåg eller annan signal, medan 24-bitarsekvivalenten ser vackert jämn ut och har högre upplösning. Det är ett enkelt visuellt hjälpmedel, men ett som bygger på okunskap om ämnet och vetenskapen för att leda konsumenterna till fel slutsatser.
För att någon ska bita huvudet av mig, så är det tekniskt sett så att dessa trappstegsexempel i viss mån korrekt skildrar ljud i den digitala domänen. Men en stamdiagram/ollipopdiagram är en mer exakt grafik för visuell provtagning av ljud än dessa trappsteg. Tänk på det så här – ett prov innehåller en amplitud vid en mycket specifik tidpunkt, inte en amplitud som hålls under en specifik tidslängd.

Användningen av trappgrafer är medvetet vilseledande när stamdiagram ger en mer korrekt representation av digitalt ljud. Dessa två grafer visar samma datapunkter men trappdiagrammet verkar mycket mindre exakt.
Det är dock korrekt att en analog till digital omvandlare (ADC) måste passa in en oändlig analog ljudsignal i ett ändligt antal bitar. En bit som faller mellan två nivåer måste avrundas till närmaste approximation, vilket kallas kvantiseringsfel eller kvantiseringsbrus. (Kom ihåg detta, eftersom vi kommer att återkomma till det.)
Hursomhelst, om du tittar på ljudutgången från någon digital-analog ljudomvandlare (DAC) som byggts det här århundradet (och förmodligen långt innan dess), kommer du inte att upptäcka några trappsteg. Inte ens om man matar ut en 8-bitars signal. Så vad är det som händer?

En 8-bitars, 10 kHz sinusvågsutgång fångad från en billig Pixel 3a-smartphone. Vi kan se en del brus men inga märkbara trappsteg som så ofta skildras av ljudföretag.
För det första är det som de här trappstegsdiagrammen beskriver, om vi tillämpar dem på en ljudutgång, något som kallas för en DAC med nollordning. Detta är en mycket enkel och billig DAC-teknik där en signal växlas mellan olika nivåer varje nytt sampel för att ge en utgång. Detta används inte i några professionella eller halvbra konsumentljudprodukter. Du kanske hittar den i en mikrokontroller för 5 dollar, men definitivt inte någon annanstans. Att förvränga ljudutgångar på detta sätt innebär en förvrängd, felaktig vågform, men det är inte vad du får.

I verkligheten är en modern ∆Σ DAC-utgång en översamplad 1-bitars PDM-signal (till höger), snarare än en nollhållningssignal (till vänster). Den senare ger en analog utgång med lägre brus när den filtreras.
Audioklassade ADC:er och DAC:er är huvudsakligen baserade på delta-sigma (∆Σ)-modulering. Komponenter av denna kaliber omfattar interpolering och översampling, brusformning och filtrering för att jämna ut och minska bruset. Delta-sigma DAC:er omvandlar ljudprover till en 1-bit ström (pulse-density modulation) med en mycket hög samplingsfrekvens. När detta filtreras ger det en jämn utgångssignal med brus som skjuts långt bort från hörbara frekvenser.
I ett nötskal: moderna DAC:er ger inte ut grova, ojämna ljudprover – de ger ut en bitström som är brusfiltrerad till en mycket noggrann, jämn utgångssignal. Den här trappstegsvisualiseringen är fel på grund av något som kallas ”kvantiseringsbrus.”
Förståelse av kvantiseringsbrus
I alla ändliga system förekommer avrundningsfel. Det är sant att en 24-bitars ADC eller DAC kommer att ha ett mindre avrundningsfel än en 16-bitars motsvarighet, men vad betyder det egentligen? Ännu viktigare, vad hör vi egentligen? Är det distorsion eller fuzz, går detaljerna förlorade för alltid?
Det är faktiskt lite av båda beroende på om du befinner dig i den digitala eller analoga världen. Men nyckelbegreppet för att förstå båda är att få grepp om brusgolvet och hur detta förbättras när bitdjupet ökar. För att demonstrera detta tar vi ett steg tillbaka från 16 och 24 bitar och tittar på mycket små exempel på bitdjup.
Skillnaden mellan 16 och 24 bitdjup är inte noggrannheten i vågformens form, utan den tillgängliga gränsen innan det digitala bruset stör vår signal.
Det finns en hel del saker att kolla upp i exemplet nedan, så först en snabb förklaring av vad vi tittar på. Vi har våra ingående (blå) och kvantiserade (orange) vågformer i de övre diagrammen, med bitdjup på 2, 4 och 8 bitar. Vi har också lagt till en liten mängd brus till vår signal för att bättre simulera verkligheten. I botten har vi en graf över kvantiseringsfelet eller avrundningsbruset, som beräknas genom att subtrahera den kvantiserade signalen från insignalen.

Kvantiseringsbruset ökar ju mindre bitdjupet är, genom avrundningsfel.
Om bitdjupet ökar blir den kvantiserade signalen helt klart en bättre överensstämmelse med insignalen. Det är dock inte det som är viktigt, observera den mycket större fel/brus-signalen för de lägre bitdjupen. Den kvantiserade signalen har inte tagit bort data från vår indata, den har faktiskt lagt in den felsignalen. Additiv syntes säger oss att en signal kan reproduceras genom summan av två andra signaler, inklusive signaler i obalans som fungerar som subtraktion. Det är så som brusavlägsnande fungerar. Så dessa avrundningsfel introducerar en ny bullersignal.
Detta är inte bara teoretiskt, man kan faktiskt höra mer och mer buller i ljudfiler med lägre bitdjup. För att förstå varför kan du undersöka vad som händer i 2-bitarsexemplet med mycket små signaler, till exempel före 0,2 sekunder. Klicka här för en inzoomad grafik. Mycket små förändringar i ingångssignalen ger stora förändringar i den kvantiserade versionen. Detta är avrundningsfelet i aktion, som har effekten att det förstärker bruset från små signaler. Så återigen blir bruset starkare när bitdjupet minskar.
Kvantisering tar inte bort data från vår indata, utan lägger faktiskt till en bullrig felsignal.
Tänk på det här i omvänd ordning också: det är inte möjligt att fånga upp en signal som är mindre än storleken på kvantiseringssteget – ironiskt nog känt som den minst signifikanta biten. Små signalförändringar måste hoppa upp till närmaste kvantiseringsnivå. Större bitdjup har mindre kvantiseringssteg och därmed mindre nivåer av brusförstärkning.
Det viktigaste är dock att notera att kvantiseringsbrusets amplitud förblir konstant, oavsett amplitud på insignalerna. Detta visar att brus förekommer på alla de olika kvantiseringsnivåerna, så det finns en konsekvent nivå av brus för varje given bitdjup. Större bitdjup ger mindre brus. Vi bör därför tänka på skillnaderna mellan 16 och 24 bitdjup inte som noggrannheten i en vågforms form, utan som den tillgängliga gränsen innan digitalt brus stör vår signal.
Bitdjup handlar om brus
När vi nu pratar om bitdjup i termer av brus, låt oss gå tillbaka till vår ovanstående grafik en sista gång. Lägg märke till hur 8-bitars exemplet ser ut som en nästan perfekt matchning för vår bullriga insignal. Detta beror på att dess 8-bitars upplösning faktiskt är tillräcklig för att fånga nivån på bakgrundsbruset. Med andra ord: kvantiseringsstegstorleken är mindre än brusets amplitud, eller så är signal-brusförhållandet (SNR) bättre än bakgrundsbrusnivån.
Ekvationen 20log(2n), där n är bitdjupet, ger oss SNR. En 8-bitarssignal har ett SNR på 48 dB, 12-bitar är 72 dB, medan 16-bitar når 96 dB och 24-bitar hela 144 dB. Detta är viktigt eftersom vi nu vet att vi bara behöver en bitdjup med tillräckligt SNR för att tillgodose det dynamiska intervallet mellan vårt bakgrundsbrus och den högsta signal vi vill fånga för att återge ljudet så perfekt som det uppträder i den verkliga världen. Det blir lite knepigt att gå från de relativa skalorna i den digitala världen till de ljudtrycksbaserade skalorna i den fysiska världen, så vi ska försöka hålla det enkelt.
Vi behöver en bitdjup med tillräckligt SNR för att ta hänsyn till vårt bakgrundsbrus för att fånga upp vårt ljud så perfekt som det låter i den verkliga världen.
Ditt öra har en känslighet som sträcker sig från 0dB (tystnad) till cirka 120dB (smärtsamt högt ljud), och den typiska förmågan att urskilja volymer ligger bara 1dB ifrån varandra. Ditt örats dynamiska omfång är alltså ungefär 120 dB, eller nära 20 bitar.
Det går dock inte att höra allt detta på en gång, eftersom trumhinnan, eller trumhinnan, dras åt för att minska den volym som faktiskt når innerörat i högljudda miljöer. Du kommer inte heller att lyssna på musik i närheten av så här högljudd, för då blir du döv. Dessutom är de miljöer du och jag lyssnar på musik i inte så tysta som friska öron kan höra. En välbehandlad inspelningsstudio kan ta oss ner till under 20 dB för bakgrundsbrus, men att lyssna i ett livligt vardagsrum eller på bussen kommer uppenbarligen att försämra förhållandena och minska vårt behov av ett högt dynamiskt omfång.
Det mänskliga örat har ett enormt dynamiskt omfång, men bara inte allt på en gång. Maskering och hörselskydd minskar dess effektivitet.
Ovanpå allt detta: När ljudstyrkan ökar får maskering av högre frekvenser effekt i örat. Vid låga volymer på 20 till 40 dB uppstår ingen maskering förutom för ljud som ligger nära varandra i tonhöjd. Men vid 80 dB maskeras ljud under 40 dB, medan ljud under 70 dB vid 100 dB är omöjliga att höra. Öronets och lyssningsmaterialets dynamiska natur gör det svårt att ange en exakt siffra, men det verkliga dynamiska området för din hörsel ligger troligen i storleksordningen 70 dB i en genomsnittlig miljö, ner till bara 40 dB i mycket högljudda miljöer. Ett bitdjup på bara 12 bitar skulle förmodligen räcka till för de flesta, så 16-bitars CD-skivor ger oss gott om utrymme.

hyperfysik Högfrekvensmaskering uppstår vid höga lyssningsvolymer, vilket begränsar vår uppfattning av tystare ljud.
De flesta instrument och inspelningsmikrofoner ger också upphov till brus (särskilt gitarrförstärkare), även i mycket tysta inspelningsstudior. Det har också gjorts några studier om dynamiskt omfång för olika genrer, bland annat den här som visar ett typiskt dynamiskt omfång på 60 dB. Föga förvånande visade genrer med en större förkärlek för tysta partier, såsom kör, opera och piano, maximala dynamiska intervall runt 70 dB, medan ”högre” rock-, pop- och rapgenrer tenderade att ligga på 60 dB eller lägre. I slutändan produceras och spelas musik bara in med en viss grad av fidelitet.
Du kanske också känner till musikindustrins ”loudness wars”, som verkligen motverkar syftet med dagens Hi-Res-ljudformat. Kraftig användning av komprimering (som förstärker brus och dämpar toppar) minskar det dynamiska omfånget. Modern musik har betydligt mindre dynamiskt omfång än skivor från 30 år sedan. Teoretiskt sett skulle modern musik kunna distribueras med lägre bithastigheter än gammal musik. Du kan kolla det dynamiska omfånget för en rad många album här.

CD-kvalitet må vara ”bara” 16 bitar, men det är överdrivet för kvaliteten.
16 bitar är allt du behöver
Det här har varit en lång resa, men förhoppningsvis har du fått en mycket mer nyanserad bild av bitdjup, brus och dynamiskt omfång än de vilseledande trappstegsexempel som du så ofta ser.
Bit-djup handlar om brus, och ju fler databitar du har för att lagra ljud: desto mindre kvantiseringsbrus kommer att införas i din inspelning. På samma sätt kommer du också att kunna fånga upp mindre signaler mer exakt, vilket bidrar till att driva det digitala brusgolvet under inspelnings- eller lyssningsmiljön. Det är allt vi behöver bitdjup för att göra. Det finns ingen fördel med att använda enorma bitdjup för ljudmaster.
Overraskande nog räcker 12 bitar förmodligen till för en hyfsat klingande musikmaster och för att tillgodose det dynamiska omfånget i de flesta lyssningsmiljöer. Digitalt ljud transporterar dock mer än bara musik, och exempel som tal eller miljöinspelningar för TV kan använda sig av ett större dynamiskt område än vad den mesta musiken gör. Dessutom har lite utrymme för separation mellan högt och tyst aldrig skadat någon.
På det hela taget kan 16 bitar (96 dB dynamiskt omfång eller 120 dB med dithering) tillgodose ett brett spektrum av ljudtyper, liksom gränserna för den mänskliga hörseln och typiska lyssningsmiljöer. De perceptuella ökningarna av 24-bitars kvalitet är högst diskutabla om inte helt enkelt en placebo, vilket jag hoppas att jag har visat. Dessutom gör ökningen av filstorlekar och bandbredd dem onödiga. Den typ av komprimering som används för att minska filstorleken på ditt musikbibliotek eller din stream har en mycket mer märkbar inverkan på ljudkvaliteten än om det är en 16- eller 24-bitarsfil.