MesopotamisktEdit
Perioden 2700-2300 f.Kr. var den första gången som den sumeriska abakusen uppträdde, en tabell med på varandra följande kolumner som avgränsade de på varandra följande storleksordningarna i deras sexagesimala talsystem.
Vissa forskare pekar på ett tecken i babylonisk kilskrift som kan ha härletts från en avbildning av abakusen. Gamla babyloniska forskare som Carruccio anser att de gamla babylonierna ”kan ha använt abakusen för addition och subtraktion; denna primitiva anordning visade sig dock vara svår att använda för mer komplexa beräkningar”.
EgyptianEdit
Användningen av abakusen i det gamla Egypten nämns av den grekiske historikern Herodotos, som skriver att egyptierna manipulerade stenarna från höger till vänster, i motsatt riktning till den grekiska metoden från vänster till höger. Arkeologer har hittat antika skivor i olika storlekar som tros ha använts som räknare. Väggskildringar av detta instrument har dock inte upptäckts.
PersianEdit
Under det achemenidiska riket, omkring 600 f.Kr. började perserna för första gången använda abakusen. Under de parthiska, sassanidiska och iranska rikena koncentrerade sig de lärda på att utbyta kunskap och uppfinningar med länderna runt omkring dem – Indien, Kina och Romarriket, då den tros ha exporterats till andra länder.
GreekEdit
De tidigaste arkeologiska beläggen för användningen av den grekiska abakusen härrör från 500-talet f.Kr. Även Demosthenes (384 f.Kr.-322 f.Kr.) talade om behovet av att använda stenar för beräkningar som var för svåra för huvudet. I en pjäs av Alexis från 400-talet f.Kr. nämns en abakus och stenar för redovisning, och både Diogenes och Polybius nämner män som ibland stod för mer och ibland för mindre, som stenarna på en abakus. Den grekiska abakusen var ett bord av trä eller marmor som var förinställt med små räknare i trä eller metall för matematiska beräkningar. Denna grekiska abakus användes i det akemenidiska Persien, den etruskiska civilisationen, det antika Rom och, fram till franska revolutionen, i den västerländska kristna världen.
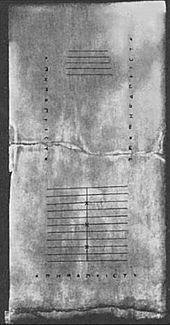
En tavla som hittades på den grekiska ön Salamis 1846 e.Kr. (Salamistavlan), daterar sig till 300 f.Kr. vilket gör den till den äldsta räknebräda som hittills har upptäckts. Det är en platta av vit marmor som är 149 cm lång, 75 cm bred och 4,5 cm tjock, på vilken det finns 5 grupper av markeringar. I mitten av tavlan finns en uppsättning av 5 parallella linjer som delas lika mycket av en vertikal linje och som kröns av en halvcirkel i skärningspunkten mellan den nedersta horisontella linjen och den enda vertikala linjen. Under dessa linjer finns ett brett utrymme med en horisontell spricka som delar det. Under denna spricka finns ytterligare en grupp av elva parallella linjer, återigen uppdelade i två delar genom en linje som är vinkelrät mot dem, men med halvcirkeln högst upp i skärningspunkten; den tredje, sjätte och nionde av dessa linjer är markerade med ett kryss där de skär den vertikala linjen. Från den här tidsramen grävdes också Darius-vasen upp 1851. Den var täckt med bilder, bland annat en ”skattmästare” som håller en vaxtavla i ena handen samtidigt som han manipulerar räknare på ett bord med den andra.
ChineseEdit

| Abacus | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Traditionell kinesiska | 算盤 | |||||||||||||||
| Simplifierad kinesiska | 算盘 | |||||||||||||||
| Bokstavligt talat betydelse | ”räknebricka” | |||||||||||||||
| Transkriptioner | Standardmandarin | Hanyu Pinyin | IPA | Yue: Kantonesiska | Yale Romanization | Jyutping | IPA | Southern Min | Hokkien POJ | Tâi-lô | ||||||
Den tidigaste kända skriftliga dokumentationen om det kinesiska abakuset härrör från det andra århundradet före Kristus.
Den kinesiska abakusen, känd som suanpan (算盤/算盘, lit. ”räknebricka”), är vanligtvis 20 cm hög och finns i olika bredder beroende på användaren. Den har vanligtvis mer än sju stavar. Det finns två pärlor på varje stav i det övre däcket och fem pärlor vardera i det nedre. Pärlorna är vanligen rundade och tillverkade av lövträ. Pärlorna räknas genom att flytta dem uppåt eller nedåt mot balken; pärlor som flyttas mot balken räknas, medan de som flyttas bort från den inte räknas. En av de övre pärlorna är 5, medan en av de nedre pärlorna är 1. Varje stav har en siffra under sig som visar platsvärdet.Suanpanen kan omedelbart återställas till utgångsläget genom en snabb rörelse längs den horisontella axeln för att snurra alla pärlor bort från den horisontella balken i mitten.
Prototypen till den kinesiska abakusen dök upp under Han-dynastin, och pärlorna är ovala. Songdynastin och tidigare använde sig av abakus av typen 1:4 eller fyra pärlor som liknar det moderna abakuset, inklusive formen på pärlorna som är allmänt kända som abakus i japansk stil.
Under den tidiga Mingdynastin började abakuset dyka upp i form av 1:5 abakus. Det övre däcket hade en pärla och det nedre hade fem pärlor.
I slutet av Mingdynastin uppträdde abakusstilarna i form av 2:5. Det övre däcket hade två pärlor och det nedre hade fem pärlor.
För Suanpan utarbetades olika beräkningstekniker som möjliggjorde effektiva beräkningar. Det finns för närvarande skolor som lär eleverna att använda den.
I den långa skriftrullen Längs floden under Qingming-festivalen målad av Zhang Zeduan under Songdynastin (960-1297) syns en suanpan tydligt bredvid en räkenskapsbok och läkarrecept på disken i ett apotek (Feibao).
Likheten mellan den romerska abakusen och den kinesiska antyder att den ena kan ha inspirerat den andra, eftersom det finns vissa bevis för handelsförbindelser mellan Romarriket och Kina. Något direkt samband kan dock inte påvisas, och likheten mellan abakusen kan vara en tillfällighet, eftersom båda i slutändan uppstod genom att räkna med fem fingrar per hand. Medan den romerska modellen (liksom de flesta moderna koreanska och japanska) har 4 plus 1 pärla per decimalplats, har den standardiserade suanpan 5 plus 2. Detta gör det möjligt att använda ett hexadecimalt siffersystem (eller vilken bas som helst upp till 18) som kan ha använts för traditionella kinesiska viktmått. (Istället för att löpa på trådar som i de kinesiska, koreanska och japanska modellerna löper pärlorna i den romerska modellen i spår, vilket förmodligen gör aritmetiska beräkningar mycket långsammare.
En annan möjlig källa till suanpanen är kinesiska räknepinnar, som fungerade med ett decimalsystem men saknade begreppet nolla som en platshållare. Nollan introducerades troligen för kineserna under Tangdynastin (618-907) då resor i Indiska oceanen och Mellanöstern skulle ha gett dem direktkontakt med Indien, vilket gjorde att de kunde skaffa sig begreppet nollan och decimalpunkten från indiska köpmän och matematiker.
RomanEdit

Den normala beräkningsmetoden i det antika Rom, liksom i Grekland, var att flytta räknare på ett slätt bord. Ursprungligen användes stenar (calculi). Senare, och i det medeltida Europa, tillverkades jetons. Markerade linjer angav enheter, femmor, tior etc. som i det romerska siffersystemet. Detta system med ”räknestugor” fortsatte under det sena romerska imperiet och i det medeltida Europa och användes i begränsad omfattning ända in på 1800-talet. Tack vare påven Sylvester II:s återinförande av abakusen med ändringar blev den återigen allmänt använd i Europa under 1000-talet Denna abakus använde pärlor på trådar, till skillnad från de traditionella romerska räkneplattorna, vilket innebar att abakusen kunde användas mycket snabbare.
Horace, som skrev på 1000-talet f.Kr., hänvisar till vaxabakusen, en bräda som var täckt med ett tunt lager svart vax på vilket kolumner och figurer skrevs in med hjälp av en stylus.
Ett exempel på ett arkeologiskt bevis på den romerska abakusen, som här visas i en rekonstruktion, härstammar från 1000-talet e.Kr. Den har åtta långa spår med upp till fem pärlor i varje och åtta kortare spår med antingen en eller inga pärlor i varje. Spåret markerat med I anger enheter, X tiotal och så vidare upp till miljoner. Pärlorna i de kortare spåren anger femmor – fem enheter, fem tiotal osv., i huvudsak i ett tvåkvinärt kodat decimalsystem som är besläktat med de romerska siffrorna. De korta spåren till höger kan ha använts för att markera romerska ”ounces” (dvs. bråkdelar).
IndianEdit
The Abhidharmakośabhāṣya av Vasubandhu (316-396), ett sanskritverk om buddhistisk filosofi, säger att filosofen Vasumitra från andra århundradet e.Kr. sade att ”om man placerar en veke (sanskrit vartikā) på talet ett (ekāṅka) betyder det att det är ett ett, medan om man placerar veken på talet hundra betyder det att det kallas hundra, och på talet tusen betyder det att det är ett tusen”. Det är oklart exakt vad detta arrangemang kan ha varit. Redan runt 500-talet hittade indiska kontorister nya sätt att registrera innehållet i abakusen. I hinduiska texter användes termen śūnya (noll) för att beteckna den tomma kolumnen på abakusen.
JapaneseEdit

På japanska kallas abakusen soroban (算盤, そろばん, lit. ”Räknebricka”), importerad från Kina på 1300-talet. Den användes troligen av arbetarklassen ett århundrade eller mer innan den härskande klassen började, eftersom klasstrukturen inte tillät att anordningar som användes av underklassen antogs eller användes av den härskande klassen. 1/4-abakusen, som tar bort den sällan använda andra och femte pärlan blev populär på 1940-talet.
Dagens japanska abakus är av typen 1:4. Fyra pärlars abakus introducerades från Kina under Muromachi-eran. Den antar formen med det övre däcket en pärla och det nedre fyra pärlor. Den översta pärlan på det övre däcket var lika med fem och den nedre är lika med ett som den kinesiska eller koreanska abakusen, och decimaltalet kan uttryckas, så abakusen är utformad som en fyra abakus. Pärlorna är alltid i form av en diamant. Kvotdivisionen används i allmänhet i stället för divisionsmetoden; för att multiplikations- och divisionssiffrorna ska vara konsekventa används samtidigt divisionsmultiplikationen. Senare hade Japan en 3:5 abakus kallad 天三算盤, som nu finns i Ize Rongji-samlingen i Shansi Village i Yamagata City. Det fanns också abakus av typen 2:5.
Med den fyrpärliga abakusen spridd är det också vanligt att använda japanska abakus runt om i världen. Det finns också förbättrade japanska abakus på olika platser. Ett av de japansktillverkade abakus som tillverkas i Kina är ett abakus med aluminiumram av plastpärlor. Filen är bredvid de fyra pärlorna och ”clearing”-knappen, tryck på clearingknappen, sätt omedelbart den övre pärlan till det övre läget, den nedre pärlan är uppringd till det nedre läget, omedelbart clearing, lätt att använda.
Abakusen tillverkas fortfarande i Japan i dag, även med spridningen, det praktiska och överkomliga priset på elektroniska miniräknare i fickformat. Användningen av soroban lärs fortfarande ut i japanska grundskolor som en del av matematiken, främst som ett hjälpmedel för snabbare mental beräkning. Med hjälp av visuella bilder av en soroban kan man komma fram till svaret på samma tid som, eller till och med snabbare än vad som är möjligt med ett fysiskt instrument.
KoreanEdit
Den kinesiska abakusen migrerade från Kina till Korea omkring 1400 e.Kr. Koreanerna kallar det för jupan (주판), supan (수판) eller jusan (주산). 4-pärlars abakus( 1:4 ) infördes till Korea Goryeo Dynasty från Kina under Song Dynasty, senare infördes 5-pärlars abakus (5:1) abakus till Korea från Kina under Ming Dynasty.
Native AmericanEdit


Vissa källor nämner användningen av ett abakus som kallas nepohualtzintzin i den gamla aztekiska kulturen. Denna mesoamerikanska abakus använde ett femsiffrigt bas-20-system. ordet Nepōhualtzintzin kommer från nahuatl och bildas av rötterna; Ne – personlig -; pōhual eller pōhualli – kontot -; och tzintzin – små liknande element. Dess fullständiga innebörd togs som: räkna med små liknande element av någon. Dess användning lärdes ut i Calmecac till temalpouhqueh , som var elever som var dedikerade till att ta räkenskaperna av himlen, från barndomen.
Nepōhualtzintzin var uppdelad i två huvuddelar som skiljdes åt av en bar eller ett mellanliggande snöre. I den vänstra delen fanns fyra pärlor, som i den första raden har enhetliga värden (1, 2, 3 och 4), och i den högra delen fanns tre pärlor med värden på 5, 10 respektive 15. För att veta värdet av respektive pärlor i de övre raderna räcker det att multiplicera med 20 (av varje rad), värdet av motsvarande konto i den första raden.
Totalt fanns det 13 rader med 7 pärlor i var och en av dem, vilket utgjorde 91 pärlor i varje Nepōhualtzintzin. Detta var ett grundläggande tal för att förstå, 7 gånger 13, ett nära samband tänkt mellan naturfenomen, underjorden och himlarnas cykler. En Nepōhualtzintzin (91) representerade antalet dagar som en årstid på året varar, två Nepōhualtzintzin (182) är antalet dagar i majsens cykel, från sådd till skörd, tre Nepōhualtzintzin (273) är antalet dagar i en babys dräktighet, och fyra Nepōhualtzintzin (364) fullbordar en cykel och motsvarar ungefär ett år (11/4 dagar kort). Översatt till modern datoraritmetik uppgick Nepōhualtzintzin till rang från 10 till 18 i floating point, som beräknade såväl stellära som infinitesimala belopp med absolut precision, vilket innebar att ingen avrundning var tillåten.
Den återupptäckten av Nepōhualtzintzin berodde på den mexikanske ingenjören David Esparza Hidalgo, som under sina vandringar i Mexiko hittade diverse gravyrer och målningar av detta instrument och rekonstruerade flera av dem gjorda i guld, jade, sköldpaddsinklädnader osv. Det har också hittats mycket gamla Nepōhualtzintzin som tillskrivs Olmec-kulturen, och till och med några armband av mayaursprung, samt en mångfald av former och material från andra kulturer.
George I. Sanchez, ”Arithmetic in Maya”, Austin-Texas, 1961 hittade en annan bas 5, bas 4 abakus på Yucatánhalvön som också beräknade kalenderdata. Detta var en fingerabakus, på ena handen användes 0, 1, 2, 3 och 4 och på andra handen användes 0, 1, 2 och 3. Notera användningen av noll i början och slutet av de två cyklerna. Sanchez arbetade med Sylvanus Morley, en känd mayaforskare.
Inkafolkets quipu var ett system av färgade knutna snören som användes för att registrera numeriska data, likt avancerade tallypinnar – men som inte användes för att utföra beräkningar. Beräkningar utfördes med hjälp av en yupana (quechua för ”räkneverktyg”; se figur) som fortfarande användes efter erövringen av Peru. Principen för hur en yupana fungerar är okänd, men 2001 föreslog den italienske matematikern Nicolino De Pasquale en förklaring av den matematiska grunden för dessa instrument. Genom att jämföra formen på flera yupanas fann forskarna att beräkningarna baserades på Fibonacci-sekvensen 1, 1, 2, 3, 5 och potenser av 10, 20 och 40 som platsvärden för de olika fälten i instrumentet. Att använda Fibonacci-sekvensen skulle hålla antalet korn inom ett och samma fält på ett minimum.
RussianEdit

Det ryska abakuset, schoty (ryska: счёты, plural från ryska: счёт, räkna), har vanligtvis ett enda snedställt däck, med tio pärlor på varje tråd (utom en tråd, vanligtvis placerad nära användaren, med fyra pärlor för bråkdelar i kvartsrubel). Äldre modeller har ytterligare en tråd med fyra pärlor för kvarts-kopeks, som präglades fram till 1916. Den ryska abakusen används ofta vertikalt, med varje tråd från vänster till höger som rader i en bok. Trådarna är vanligtvis böjda så att de böljar uppåt i mitten, för att hålla pärlorna fast på någon av de två sidorna. Den rensas när alla pärlor flyttas till höger. Under manipuleringen flyttas pärlorna till vänster. För att underlätta visningen har de två mittersta pärlorna på varje tråd (den femte och sjätte pärlan) vanligtvis en annan färg än de övriga åtta pärlorna. På samma sätt kan den vänstra pärlan på tusentalstråden (och miljontråden, om den finns) ha en annan färg.
Som en enkel, billig och pålitlig anordning användes den ryska abakusen i alla affärer och på alla marknader i hela f.d. Sovjetunionen, och användningen av den lärdes ut i de flesta skolor fram till 1990-talet. Inte ens 1874 års uppfinning av den mekaniska kalkylatorn, Odhners aritmometer, hade ersatt dem i Ryssland; enligt Jakov Perelman var det till och med på hans tid känt att vissa affärsmän som försökte importera sådana apparater till det ryska imperiet gav upp och lämnade landet i förtvivlan efter att ha fått se en skicklig abakusoperatörs arbete. Likaså har massproduktionen av Felix aritmometrar sedan 1924 inte minskat användningen av dem nämnvärt i Sovjetunionen. Den ryska abakusen började förlora i popularitet först efter att massproduktionen av mikrokalkylatorer hade börjat i Sovjetunionen 1974. Idag betraktas den som en arkaism och har ersatts av den handhållna miniräknaren.
Den ryska abakusen fördes till Frankrike omkring 1820 av matematikern Jean-Victor Poncelet, som tjänstgjorde i Napoleons armé och hade varit krigsfånge i Ryssland. Abakusen hade fallit ur bruk i Västeuropa på 1500-talet i och med framväxten av decimalnotering och algoritmiska metoder. För Poncelets franska samtida var det något nytt. Poncelet använde den, inte för något tillämpat ändamål, utan som ett hjälpmedel för undervisning och demonstrationer. Turkarna och armenierna använde också abakus som liknade den ryska schoty. Den kallades coulba av turkarna och choreb av armenierna.