A Concise Introduction to Logic

9.1 Ett historiskt exempel

Filosofen David Hume (1711-1776) är ihågkommen för att ha varit en lysande skeptisk empirist. En person är skeptiker när det gäller ett ämne om personen både har mycket strikta normer för vad som utgör kunskap om det ämnet och också tror att vi inte kan uppfylla dessa strikta normer. Empirism är uppfattningen att vi i första hand får kunskap genom erfarenhet, särskilt erfarenheter från våra sinnen. I sin bok, An Inquiry Concerning Human Understanding, lägger Hume fram sina principer för kunskap och råder oss sedan att städa upp i våra bibliotek:

När vi kör över biblioteken, övertygade om dessa principer, vilken förödelse måste vi då åstadkomma? Om vi till exempel tar i vår hand någon volym av gudomlighet eller skolmetafysik, låt oss fråga: Innehåller den något abstrakt resonemang om kvantitet eller antal? Nej. Innehåller den några experimentella resonemang om fakta och existens? Nej. Lämna den då till lågorna, för den kan inte innehålla något annat än sofisteri och illusioner.

Hume ansåg att de enda källorna till kunskap var logiska eller matematiska resonemang (som han ovan kallar ”abstrakta resonemang om kvantitet eller antal”) eller sinneserfarenheter (”experimentella resonemang om sakförhållanden och existens”). Hume föranleds att hävda att alla påståenden som inte baseras på den ena eller andra metoden är värdelösa.

Vi kan rekonstruera Humes argumentation på följande sätt. Anta att t är något ämne som vi hävdar att vi har kunskap om. Anta att vi inte har fått denna kunskap genom erfarenhet eller logik. Skrivet på engelska kan vi rekonstruera hans argument på följande sätt:

Vi har kunskap om t om och endast om våra påståenden om t är inlärda från experimentella resonemang eller från logik eller matematik.

Våra påståenden om t lär vi oss inte genom experimentella resonemang.

Våra påståenden om t lär vi oss inte genom logik eller matematik.

Vi har ingen kunskap om t.

Vad betyder frasen ”om och endast om”? Filosofer menar att den, och flera synonyma fraser, används ofta i resonemang. Om vi lämnar ”om och endast” oförklarat för tillfället kan vi använda följande översättningsnyckel för att skriva upp argumentet i en blandning av vår påståendelogik och engelska.

P: Vi har kunskap om t.

Q: Våra påståenden om t har vi lärt oss genom experimentella resonemang.

R: Våra påståenden om t har vi lärt oss från logik eller matematik.

Och så har vi:

P om och endast om (QvR)

¬Q

¬R

¬P

Vår uppgift är att till vårt logiska språk lägga till en motsvarighet till ”om och endast om”. Därefter kan vi utvärdera denna omformulering av Humes argument.

9.2 Det bikonditionella

Innan vi introducerar en symbol som är synonym med ”om och endast om”, och sedan lägger ut dess syntax och semantik, bör vi börja med en observation. En fras som ”P om och endast om Q” verkar vara ett förkortat sätt att säga ”P om Q och P endast om Q”. När vi väl har noterat detta behöver vi inte försöka urskilja innebörden av ”if and only if” med hjälp av vår expertförståelse av engelska. Istället kan vi urskilja innebörden av ”if and only if” med hjälp av våra redan rigorösa definitioner av ”if”, ”and” och ”only if”. Specifikt kommer ”P om Q och P endast om Q” att översättas med ”((Q→P)^(P→Q))”. (Om detta är oklart för dig kan du gå tillbaka och läsa igenom avsnitt 2.2.) Låt oss nu göra en sanningstabell för denna formel.

P	Q	(Q → P)	(P → Q)	((Q→P)^(P→Q))
T	T	T	T	T
T	F	T	F	F
F	T	F	T	F
F	F	T	T	T

Vi har fastställt semantiken för ”om och endast om”. Vi kan nu införa en ny symbol för detta uttryck. Det är traditionellt att använda dubbelpilen, ”↔”. Vi kan nu uttrycka syntaxen och semantiken för ”↔”.

Om Φ och Ψ är meningar, då

(Φ↔Ψ)

är en mening. Denna typ av mening kallas vanligtvis för en ”bikonditionell”.

Semantiken ges av följande sanningstabell.

.

Φ	Ψ	(Φ↔Ψ)
T	T	T
T	F	F
F	T	F
F	F	T

Ett glädjande resultat av vår redogörelse för bikonditionalitet är att den gör det möjligt för oss att kortfattat förklara det syntaktiska begreppet logisk ekvivalens. Vi säger att två meningar Φ och Ψ är ”ekvivalenta” eller ”logiskt ekvivalenta” om (Φ↔Ψ) är en sats.

9.3 Alternativa fraser

På engelska verkar det som om det finns flera fraser som vanligen har samma betydelse som bikonditional. Var och en av följande meningar skulle översättas med (P↔Q).

P om och endast om Q.

P bara om Q.

P är nödvändig och tillräcklig för Q.

P är likvärdig med Q.

9.4 Resonera med bikonditionaliteten

Hur kan vi resonera med hjälp av en bikonditionalitet? Till en början verkar det som om den inte ger någon större vägledning. Om jag vet att (P↔Q) vet jag att P och Q har samma sanningsvärde, men enbart utifrån den meningen vet jag inte om de båda är sanna eller falska. Trots detta kan vi dra nytta av semantiken för bikonditionalitet för att observera att om vi också känner till sanningsvärdet för en av de meningar som utgör bikonditionalitet kan vi härleda sanningsvärdet för den andra meningen. Detta ger upphov till en enkel uppsättning regler. Det kommer i själva verket att handla om fyra regler, men vi kommer att samla dem under ett enda namn, ”ekvivalens”:

och

och

och

Vad händer om vi istället försöker visa ett bikonditionellt? Här kan vi återvända till insikten att bikonditionalen (Φ↔Ψ) är likvärdig med ((Φ→Ψ)^(Ψ→Φ)). Om vi kan bevisa både (Φ→Ψ) och (Ψ→Φ) vet vi att (Φ↔Ψ) måste vara sant.

Vi kan kalla denna regel för ”bikondition”. Den har följande form:

(Φ→Ψ)

(Ψ→Φ)

(Φ↔Ψ)

Detta innebär att vi ofta, när vi har som mål att bevisa ett bikonditionellt villkor, kommer att genomföra två konditionsavledningar för att härleda två konditionella påståenden och sedan använda regeln om bikondition. Det vill säga, många bevis för bikonditionaler har följande form:

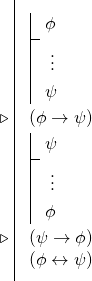
9.5 Återgå till Hume

Vi kan nu se om vi kan bevisa Humes argument. Givet nu den nya bikonditionella symbolen kan vi börja ett direkt bevis med våra tre premisser.

Vi har redan observerat att vi tror att (QvR) är falsk eftersom ¬Q och ¬R. Så låt oss bevisa ¬(QvR). Denna mening kan inte bevisas direkt, med tanke på de premisser vi har, och den kan inte bevisas med ett villkorligt bevis, eftersom den inte är ett villkor. Så låt oss försöka med ett indirekt bevis. Vi tror att ¬(QvR) är sann, så vi antar att detta förnekas och visar en motsägelse.

Humes argument, åtminstone så som vi har rekonstruerat det, är giltigt.

Är Humes argument giltigt? Huruvida det är giltigt beror på den första förutsättningen ovan (eftersom den andra och tredje förutsättningen är abstraktioner om något ämne t). Mer specifikt beror det på påståendet att vi har kunskap om något bara för att vi kan visa det med experiment eller logik. Hume hävdar att vi bör misstro – ja, vi bör bränna texter som innehåller påståenden som inte kommer från experiment och observation eller från logik och matematik. Men betänk detta påstående: Vi har kunskap om ett ämne t om och endast om våra påståenden om t är lärda från experiment eller om våra påståenden om t är lärda från logik eller matematik.

Otäckte Hume detta påstående genom experiment? Eller upptäckte han det genom logik? Vilket öde skulle Humes bok drabbas av om vi följde hans råd?

9.6 Några exempel

Det kan vara till hjälp att bevisa några satser som använder sig av bikonditionalitet, för att illustrera hur vi kan resonera med bikonditionalitet.

Här är en användbar princip. Om två meningar har samma sanningsvärde som en tredje mening, så har de samma sanningsvärde som varandra. Vi anger detta som (((P↔Q)^(R↔Q))→(P↔R)). För att illustrera resonemang med bikonditionalitet, låt oss bevisa denna sats.

Denna sats är ett villkor, så den kommer att kräva en villkorlig härledning. Konsekvensen av villkoret är en bikonditionell, så vi kommer att förvänta oss att behöva två villkorliga härledningar, en för att bevisa (P→R) och en för att bevisa (R→P). Beviset kommer att se ut så här. Studera det noga.

Vi har tidigare nämnt de principer som vi förknippar med matematikern Augustus De Morgan (1806-1871) och som i dag kallas ”De Morgans lagar” eller ”De Morgans ekvivalenser”. Dessa är erkännandet att ¬(PvQ) och (¬P^¬Q) är likvärdiga, och även att ¬(P^Q) och (¬Pv¬Q) är likvärdiga. Vi kan nu uttrycka dessa med bikonditionalitet. Följande är satser i vår logik:

(¬(PvQ)↔(¬P^¬Q))

(¬(P^Q)↔(¬Pv¬Q))

Vi ska bevisa den andra av dessa satser. Detta är kanske det svåraste beviset vi har sett; det kräver inbäddade indirekta bevis och en hel del smarthet för att hitta vad den relevanta motsägelsen kommer att vara.

9.7 Användning av satser

Varje mening i vår logik är, i semantiska termer, av ett av tre slag. Den är antingen en tautologi, en motsägelsefull mening eller en betingad mening. Vi har redan definierat ”tautologi” (en mening som måste vara sann) och ”motsägelsefull mening” (en mening som måste vara falsk). En kontingent mening är en mening som varken är en tautologi eller en motsägelsefull mening. En kontingent mening är alltså en mening som kan vara sann eller falsk.

Här är ett exempel på varje typ av mening:

(Pv¬P)

(P↔¬P)

P

P

Den första är en tautologi, den andra är en motsägelsefull mening och den tredje är kontingent. Vi kan se detta med hjälp av en sanningstabell.

.

P	¬P	(Pv¬P)	(P↔¬P)	P
T	F	T	F	T
F	T	T	F	F

Observera att negationen av en tautologi är en motsägelse, negationen av en motsägelse är en tautologi, och negationen av en kontingent mening är en kontingent mening.

¬(Pv¬P)

¬(P↔¬P)

¬P

.

P	¬P	(Pv¬P)	¬(Pv¬P)	¬(Pv¬P)	(P↔¬P)	¬(P↔¬P)
T	F	T	F	F	F	T
F	T	T	F	F	T

Ett ögonblicks eftertanke kommer att avslöja att det skulle vara en riktig katastrof om antingen en motsägelsefull mening eller en betingad mening var en sats i vår satslogik. Vår logik har utformats för att endast producera giltiga argument. Argument som inte har några premisser, konstaterade vi, bör ha slutsatser som måste vara sanna (återigen, detta följer av att en mening som kan bevisas utan premisser kan bevisas med vilka premisser som helst, och därför är det bäst att den är sann oavsett vilka premisser vi använder). Om en sats var motsägelsefull skulle vi veta att vi kunde bevisa en osanning. Om en sats är kontingent kan vi ibland bevisa en osanning (dvs. vi kan bevisa en mening som under vissa förutsättningar är falsk). Och med tanke på att vi har antagit indirekt härledning som bevismetod följer att när vi väl har en motsägelse eller en motsägelsefull mening i ett argument kan vi bevisa vad som helst.

Satser kan vara mycket användbara för oss i argument. Anta att vi vet att varken Smith eller Jones kommer att åka till London, och vi vill därför bevisa att Jones inte kommer att åka till London. Om vi tillåter oss att använda ett av De Morgans teorem kan vi snabbt klara av argumentet. Anta följande nyckel:

P: Smith kommer att åka till London.

Q: Jones kommer att åka till London.

Och vi har följande argument:

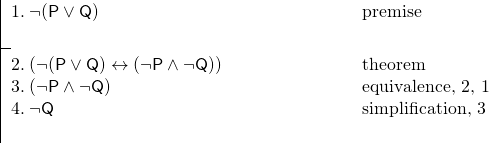
Det här beviset gjordes mycket enkelt genom att vi använde oss av satsen på rad 2.

Det finns två saker att notera om detta. För det första bör vi tillåta oss själva att göra detta, för om vi vet att en mening är en sats, så vet vi att vi kan bevisa den satsen i ett underbevis. Det vill säga, vi skulle kunna ersätta rad 2 ovan med ett långt underbevis som bevisar (¬(P v Q)↔(¬P ^ ¬Q))), som vi sedan skulle kunna använda. Men om vi är säkra på att (¬(P v Q)↔(¬P ^ ¬Q)) är en sats bör vi inte behöva göra detta bevis om och om igen, varje gång vi vill använda oss av satsen.

Den andra frågan som vi bör inse är mer subtil. Det finns oändligt många meningar av samma form som vår sats, och vi borde kunna använda även dessa. Till exempel skulle följande meningar var och en ha ett bevis som är identiskt med vårt bevis för satsen (¬(P v Q)↔(¬P ^ ¬Q)), förutom att bokstäverna skulle vara olika:

(¬(R v S) ↔ (¬R ^ ¬S))

(¬(T v U) ↔ (¬T ^ ¬U))

(¬(V v W) ↔ (¬V ^ ¬W))

Detta är förhoppningsvis uppenbart. Ta beviset för (¬(P v Q)↔(¬P ^ ¬Q)), och ersätt i det beviset varje instans av P med R och varje instans av Q med S, och du skulle få ett bevis för (¬(R v S)↔(¬R ^ ¬S)).

Men här är något som kanske är mindre uppenbart. Var och en av följande kan betraktas som liknande satsen (¬(P v Q)↔(¬P ^ ¬Q)).

(¬((P^Q) v (R^S))↔(¬(P^Q) ^ ¬(R^S)))

(¬(T v (Q v V))↔(¬T ^ ¬(Q v V))

(¬((Q↔P) v (¬R→¬Q))↔(¬(Q↔P) ^ ¬(¬R→¬Q)))

Till exempel, om man tog ett bevis för (¬(P v Q)↔(¬P ^ ¬Q)) och ersatte varje initial instans av P med (Q↔P) och varje initial instans av Q med (¬R→¬Q), skulle man få ett bevis för satsen (¬((Q↔P) v (¬R→¬Q))↔(¬(Q↔P) ^ ¬(¬R→¬Q))).

Vi kan fånga denna insikt på två sätt. Vi skulle kunna ange teorem i vårt metallspråk och tillåta att dessa har instanser. Vi skulle alltså kunna ta (¬(Φ v Ψ) ↔ (¬Φ ^ ¬Ψ)) som en sats i metallspråket, där vi skulle kunna ersätta varje Φ med en mening och varje Ψ med en mening och få en särskild instans av en sats. Ett alternativ är att tillåta att vi från en sats kan producera andra satser genom substitution. För enkelhetens skull kommer vi att välja denna andra strategi.

Vår regel kommer att vara följande. När vi väl har bevisat en sats kan vi när som helst citera den i ett bevis. Vår motivering är att påståendet är en sats. Vi tillåter substitution av en atomär sats i satsen med en annan sats om och endast om vi ersätter varje inledande instans av den atomära satsen i satsen med samma sats.

Innan vi tar upp ett exempel är det fördelaktigt att räkna upp några användbara satser. Det finns oändligt många teorem i vårt språk, men dessa tio är ofta mycket användbara. Några av dem har vi bevisat. De andra kan bevisas som en övning.

T1 (P v ¬P)

T2 (¬(P→Q) ↔ (P^¬Q))

T3 (¬(P v Q) ↔ (¬P ^ ¬Q))

T4 ((¬P v ¬Q) ↔ ¬(P ^ Q))

T5 (¬(P ↔ Q) ↔ (P ↔ ¬Q))

T6 (¬P → (P → Q))

T7 (P → (Q → P))

T8 ((P→(Q→R)) → ((P→Q) → (P→R)))

T9 ((¬P→¬Q) → ((¬P→Q) →P))

T10 ((P→Q) → (¬Q→¬P))

Några exempel kommer att göra fördelen med att använda satser tydlig. Betrakta ett annat argument som bygger på det ovanstående. Vi vet att det varken är så att om Smith åker till London kommer han att åka till Berlin, eller att om Jones åker till London kommer han att åka till Berlin. Vi vill bevisa att det inte är så att Jones kommer att åka till Berlin. Vi lägger till följande till vår nyckel:

R: Smith kommer att åka till Berlin.

S: Jones kommer att åka till Berlin.

Och vi har följande argument:

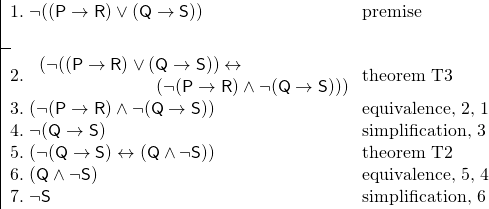
Användningen av satser gjorde det här beviset mycket kortare än det annars skulle ha varit. Dessutom gör teorem ofta ett bevis lättare att följa, eftersom vi känner igen teoremen som tautologier – som meningar som måste vara sanna.

9.8 Problem

1. Bevisa att vart och ett av följande argument är giltigt.

1. Premisser: P, ¬Q. Slutsats: Slutsats: ¬(P↔Q).
2. Premisser: (¬PvQ), (Pv¬Q). Slutsats: (P↔Q).
3. Premisserna: (P↔Q).
4. Premisserna: (P↔Q): (P↔Q), (R↔S) . Slutsats: ((P^R)↔(Q^S)).

1. Bevisa var och en av följande satser.

1. T1
2. T2
3. T5
4. T6
5. T7
6. T8
7. T9
8. ((P^Q)↔¬(¬Pv¬Q))
9. ((P→Q)↔¬(P^¬Q))

1. Skriv på normal vardaglig engelska ett eget giltigt argument med minst två premisser, varav minst en är en bikonditionell. Ditt argument ska bara vara ett stycke (inte en ordnad lista med meningar eller något annat som ser ut som formell logik). Översätt det till påståendelogik och bevisa att det är giltigt.
2. Skriv på normal vardaglig engelska ett eget giltigt argument med minst två premisser och med en slutsats som är en bikonditionell. Ditt argument ska bara vara ett stycke (inte en ordnad lista med meningar eller något annat som ser formellt ut som logik). Översätt det till påståendelogik och bevisa att det är giltigt.