Răspuns 7 – 7 – 7 – 7 = 73 Se citește „șapte la cub.”

Înțelegerea exponenților și a rădăcinilor pătrate

Obiectivul (obiectivele) de învățare

– Evaluați expresii care conțin exponenți.

– Scrieți factori repetați folosind notația exponențială.

– Găsiți o rădăcină pătrată a unui pătrat perfect.

Exponenții oferă un mod special de a scrie înmulțiri repetate. Numerele scrise în acest mod au o formă specifică, fiecare parte furnizând informații importante despre număr. Scrierea numerelor folosind exponenți poate economisi, de asemenea, mult spațiu. Operația inversă de înmulțire a unui număr cu el însuși se numește găsirea rădăcinii pătrate a unui număr. Această operație este utilă pentru problemele legate de aria unui pătrat.

Notația exponențială este un mod special de a scrie factori repetați, de exemplu 7 – 7. Notația exponențială are două părți. O parte a notației se numește bază. Baza este numărul care se înmulțește cu el însuși. Cealaltă parte a notației este exponentul, sau puterea. Acesta este numărul mic scris sus, în dreapta bazei. Exponentul, sau puterea, indică de câte ori trebuie folosită baza ca factor în înmulțire. În exemplul de mai sus, 7 – 7 poate fi scris ca 72, 7 este baza și 2 este exponentul. Exponentul 2 înseamnă că există doi factori.

72 = 7 – 7 = 49

Puteți citi 72 ca „șapte la pătrat”. Acest lucru se datorează faptului că înmulțirea unui număr cu el însuși se numește „ridicarea la pătrat a unui număr”. În mod similar, ridicarea unui număr la o putere de 3 se numește „cubarea numărului”. Puteți citi 73 ca „șapte la cub.”

Puteți citi 25 ca „doi la puterea a cincea” sau „doi la puterea cinci”. Citiți 84 ca „opt la puterea a patra” sau „opt la puterea a patra”. Acest format poate fi utilizat pentru a citi orice număr scris în notație exponențială. De fapt, în timp ce 63 se citește cel mai frecvent „șase la cub”, poate fi citit și „șase la puterea a treia” sau „șase la puterea a treia.”

Pentru a afla valoarea unui număr scris în formă exponențială, rescrieți numărul ca o înmulțire repetată și efectuați înmulțirea. Două exemple sunt prezentate mai jos.

Găsește valoarea lui 43.

A) 12

B) 64

C) 256

D) 43

Scrierea înmulțirii repetate în notație exponențială poate economisi timp și spațiu. Luați în considerare exemplul 5 – 5 – 5 – 5 – 5 – 5. Putem folosi notația exponențială pentru a scrie această înmulțire repetată ca 54. Deoarece 5 este înmulțit, acesta este scris ca bază. Deoarece baza este folosită de 4 ori în înmulțire, exponentul este 4. Expresia 5 – 5 – 5 – 5 – 5 – 5 poate fi rescrisă în notație exponențială prescurtată ca 54 și se citește, „cinci la puterea a patra” sau „cinci la puterea 4.”

Pentru a scrie înmulțirea repetată a aceluiași număr în notație exponențială, scrieți mai întâi numărul care se înmulțește ca bază. Apoi numărați de câte ori este folosit acel număr în înmulțire și scrieți acel număr ca exponent. Asigurați-vă că numărați numerele, nu semnele de înmulțire, pentru a determina exponentul.

Scrieți 10 – 10 – 10 – 10 – 10 – 10 – 10 – 10 în notație exponențială.

A) 1.000.000

B) 60

C) 105

D) 106

Cum ați văzut mai devreme, 52 se numește „cinci la pătrat”. „Cinci la pătrat” înseamnă să înmulțești cinci cu el însuși. În matematică, numim înmulțirea unui număr cu el însuși „ridicarea la pătrat” a numărului. Numim rezultatul ridicării la pătrat a unui număr întreg un pătrat sau un pătrat perfect. Un pătrat perfect este orice număr care poate fi scris ca un număr întreg ridicat la puterea 2. De exemplu, 9 este un pătrat perfect. Un număr perfect pătrat poate fi reprezentat sub forma unui pătrat, așa cum se arată mai jos. Vedem că 1, 4, 9, 16, 25 și 36 sunt exemple de pătrate perfecte.

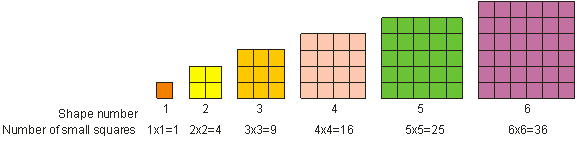
Pentru a ridica un număr la pătrat, înmulțiți numărul cu el însuși. 3 la pătrat = 32 = 3 – 3 = 9.

Mai jos sunt alte câteva exemple de pătrate perfecte.

Operația inversă de ridicare la pătrat a unui număr se numește găsirea rădăcinii pătrate a unui număr. Găsirea rădăcinii pătrate este ca și cum ai întreba: „ce număr înmulțit cu el însuși îmi va da acest număr?”. Rădăcina pătrată a lui 25 este 5, deoarece 5 înmulțit cu el însuși este egal cu 25. Rădăcinile pătrate se scriu cu ajutorul unui simbol matematic, numit semn radical, care arată astfel: . „Rădăcina pătrată a lui 25” se scrie .

Găsește .

A) 6

B) 18

C) 72

D) 7

Notația exponențială este o modalitate prescurtată de scriere a înmulțirii repetate a aceluiași număr. Un număr scris în notație exponențială are o bază și un exponent, iar fiecare dintre aceste părți oferă informații pentru găsirea valorii expresiei. Baza spune ce număr este înmulțit în mod repetat, iar exponentul spune de câte ori este folosită baza în înmulțire. Exponenții 2 și 3 au denumiri speciale. Ridicarea unei baze la o putere de 2 se numește „ridicarea la pătrat” a unui număr. Ridicarea unei baze la o putere de 3 se numește „cubarea” unui număr. Inversul ridicării la pătrat a unui număr este găsirea rădăcinii pătrate a unui număr. Pentru a găsi rădăcina pătrată a unui număr, întrebați-vă: „Ce număr pot înmulți cu el însuși pentru a obține acest număr?”

.