9.1 Un exemplu istoric
Filosoful David Hume (1711-1776) este amintit pentru că a fost un strălucit empirist sceptic. O persoană este sceptică cu privire la un subiect dacă acea persoană are atât standarde foarte stricte cu privire la ceea ce constituie cunoașterea despre acel subiect, cât și dacă crede că nu putem îndeplini aceste standarde stricte. Empirismul este punctul de vedere conform căruia dobândim cunoștințe în primul rând prin experiență, în special prin experiențele simțurilor noastre. În cartea sa, An Inquiry Concerning Human Understanding, Hume expune principiile sale pentru cunoaștere, iar apoi ne sfătuiește să ne curățăm bibliotecile:
Când alergăm peste biblioteci, convinși de aceste principii, ce ravagii trebuie să facem? Dacă luăm în mână vreun volum de divinitate sau de metafizică școlară, de exemplu, să ne întrebăm: Conține vreun raționament abstract despre cantitate sau număr? Nu. Conține vreun raționament experimental referitor la materia de fapt și la existență? Nu. Atunci aruncați-l în flăcări, pentru că nu poate conține decât sofisme și iluzii.
Hume considera că singurele surse de cunoaștere sunt raționamentul logic sau matematic (pe care îl numește mai sus „raționament abstract privind cantitatea sau numărul”) sau experiența senzorială („raționament experimental privind materia de fapt și existența”). Hume este condus să susțină că orice afirmație care nu se bazează pe una sau pe cealaltă metodă este lipsită de valoare.
Potem reconstrui argumentul lui Hume în felul următor. Să presupunem că t este un subiect despre care pretindem că avem cunoștințe. Să presupunem că nu am obținut această cunoaștere din experiență sau din logică. Scris în engleză, putem reconstrui argumentul său în felul următor:
Avem cunoștințe despre t dacă și numai dacă afirmațiile noastre despre t sunt învățate din raționamente experimentale sau din logică sau matematică.
Afirmațiile noastre despre t nu sunt învățate din raționamente experimentale.
Afirmațiile noastre despre t nu sunt învățate din logică sau matematică.
Nu avem cunoștințe despre t.
Ce înseamnă această expresie „dacă și numai dacă”? Filozofii cred că ea, precum și mai multe sintagme sinonime, sunt folosite des în raționamente. Lăsând „dacă și numai dacă” neexplicat deocamdată, putem folosi următoarea cheie de traducere pentru a scrie argumentul într-un amestec al logicii noastre propoziționale și al limbii engleze.
P: Avem cunoștințe despre t.
Q: Afirmațiile noastre despre t sunt învățate din raționamente experimentale.
R: Afirmațiile noastre despre t sunt învățate din logică sau matematică.
Și astfel avem:
P dacă și numai dacă (QvR)
¬Q
¬R
¬P
Sarcina noastră este să adăugăm limbajului nostru logic un echivalent pentru „dacă și numai dacă”. Apoi putem evalua această reformulare a argumentului lui Hume.
9.2. Bicondiționalul
Înainte de a introduce un simbol sinonim cu „dacă și numai dacă” și de a-i expune apoi sintaxa și semantica, trebuie să începem cu o observație. O frază de genul „P dacă și numai dacă Q” pare a fi un mod abreviat de a spune „P dacă Q și P numai dacă Q”. Odată ce observăm acest lucru, nu trebuie să încercăm să discernem sensul lui „dacă și numai dacă” folosind înțelegerea noastră de experți în limba engleză. În schimb, putem discerne sensul expresiei „dacă și numai dacă” folosind definițiile noastre deja riguroase de „dacă”, „și” și „numai dacă”. Mai exact, „P dacă Q și P numai dacă Q” va fi tradus „((Q→P)^(P→Q)))”. (Dacă acest lucru nu vă este clar, reveniți și revedeți secțiunea 2.2.) Acum, să realizăm un tabel de adevăr pentru această formulă.
| P | Q | (Q → P) | (P → Q) | ((Q→P)^(P→Q)) | |
| T | T | T | T | T | |
| T | F | T | T | F | F |
| F | T | F | T | T | F |
| F | F | T | T | T |
Am stabilit semantica pentru „dacă și numai dacă”. Acum putem introduce un nou simbol pentru această expresie. Este tradițional să folosim săgeata dublă, „↔”. Acum putem exprima sintaxa și semantica lui „↔”.
Dacă Φ și Ψ sunt propoziții, atunci
(Φ↔Ψ)
este o propoziție. Acest tip de propoziție se numește în mod obișnuit „bicondițional”.
Semantica este dată de următorul tabel de adevăr.
| Φ | Ψ | (Φ↔Ψ) |
| T | T | T |
| T | F | F |
| F | ||
| F | T | F |
| F | F | T |
Un rezultat plăcut al relatării noastre despre bicondițional este că ne permite să explicăm succint noțiunea sintactică de echivalență logică. Spunem că două propoziții Φ și Ψ sunt „echivalente” sau „echivalente din punct de vedere logic” dacă (Φ↔Ψ) este o teoremă.
9.3 Expresii alternative
În limba engleză, se pare că există mai multe expresii care au, de obicei, același sens ca și bicondiționalul. Fiecare dintre următoarele propoziții s-ar traduce prin (P↔Q).
P dacă și numai dacă Q.
P doar în cazul în care Q.
P este necesar și suficient pentru Q.
P este echivalent cu Q.
9.4 Raționamentul cu bicondiționalul
Cum putem raționa folosind un bicondițional? La început, ar părea să ofere puține indicații. Dacă știu că (P↔Q), știu că P și Q au aceeași valoare de adevăr, dar numai din această propoziție nu știu dacă ambele sunt ambele adevărate sau ambele false. Cu toate acestea, putem profita de semantica bicondiționalului pentru a observa că, dacă cunoaștem și valoarea de adevăr a uneia dintre propozițiile care constituie bicondiționalul, atunci putem deduce valoarea de adevăr a celeilalte propoziții. Acest lucru sugerează un set simplu de reguli. Acestea vor fi, de fapt, patru reguli, dar le vom grupa sub un singur nume, „echivalență”:
(Φ↔Ψ)
Φ
_____
Ψ
și
(Φ↔Ψ)
Ψ
_____
Φ
și
(Φ↔Ψ)
.
¬Φ
_____
¬Ψ
și
(Φ↔Ψ)
.
¬Ψ
_____
¬Φ
Ce se întâmplă dacă, în schimb, încercăm să arătăm un bicondițional? Aici ne putem întoarce la ideea că bicondiționalul (Φ↔Ψ) este echivalent cu ((Φ→Ψ)^(Ψ→Φ)). Dacă am putea demonstra atât (Φ→Ψ), cât și (Ψ→Φ), vom ști că (Φ↔Ψ) trebuie să fie adevărată.
Potem numi această regulă „bicondiție”. Ea are următoarea formă:
(Φ→Ψ)
(Ψ→Φ)
(Φ↔Ψ)
Acest lucru înseamnă că, adesea, atunci când ne propunem să demonstrăm o bicondiție, vom întreprinde două derivări condiționale pentru a obține două condiționale, iar apoi vom folosi regula bicondiției. Adică, multe demonstrații ale bicondiționalelor au următoarea formă:
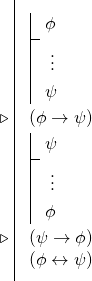
9.5. Revenind la Hume
Acum putem vedea dacă suntem capabili să demonstrăm argumentul lui Hume. Dat fiind acum noul simbol bicondițional, putem începe o demonstrație directă cu cele trei premise ale noastre.

Am observat deja că noi credem că (QvR) este falsă pentru că ¬Q și ¬R. Să demonstrăm deci că ¬(QvR). Această propoziție nu poate fi demonstrată direct, date fiind premisele pe care le avem; și nu poate fi demonstrată cu o demonstrație condițională, deoarece nu este o condițională. Așadar, să încercăm o dovadă indirectă. Credem că ¬(QvR) este adevărată, așa că vom presupune negarea acesteia și vom arăta o contradicție.

Argumentul lui Hume, cel puțin așa cum l-am reconstruit, este valid.
Este argumentul lui Hume solid? Faptul că este solid depinde de prima premisă de mai sus (deoarece a doua și a treia premisă sunt abstracțiuni despre un subiect t). Mai precis, depinde de afirmația că avem cunoștințe despre ceva doar în cazul în care putem demonstra acest lucru cu ajutorul experimentului sau al logicii. Hume susține că ar trebui să nu avem încredere – de fapt, ar trebui să ardem textele care conțin – afirmații care nu provin din experimente și observații sau din logică și matematică. Dar luați în considerare această afirmație: avem cunoștințe despre un subiect t dacă și numai dacă afirmațiile noastre despre t sunt învățate din experiment sau afirmațiile noastre despre t sunt învățate din logică sau matematică.
Hume a descoperit această afirmație prin experimente? Sau a descoperit-o prin logică? Ce soartă ar avea cartea lui Hume, dacă i-am urma sfatul?
9.6 Câteva exemple
Pot fi utile demonstrarea unor teoreme care se folosesc de bicondițional, pentru a ilustra cum putem raționa cu bicondiționalul.
Iată un principiu util. Dacă două propoziții au aceeași valoare de adevăr cu o a treia propoziție, atunci ele au aceeași valoare de adevăr una cu cealaltă. Enunțăm acest lucru sub forma ((((P↔Q)^(R↔Q))→(P↔R)). Pentru a ilustra raționamentul cu bicondiționalul, să demonstrăm această teoremă.
Această teoremă este un condițional, deci va necesita o derivare condițională. Consecventul condiționalului este un bicondițional, deci ne vom aștepta să avem nevoie de două derivări condiționale, una pentru a demonstra (P→R) și una pentru a demonstra (R→P). Demonstrația va arăta în felul următor. Studiați-o cu atenție.

Am menționat mai înainte principiile pe care le asociem cu matematicianul Augustus De Morgan (1806-1871) și care astăzi sunt numite „Legile lui De Morgan” sau „Echivalențele lui De Morgan”. Acestea constau în recunoașterea faptului că ¬(PvQ) și (¬P^¬Q) sunt echivalente și, de asemenea, că ¬(P^Q) și (¬Pv¬Q) sunt echivalente. Putem acum să le exprimăm cu ajutorul bicondiționalului. Următoarele sunt teoreme ale logicii noastre:
(¬(PvQ)↔(¬P^¬Q))
(¬(P^Q)↔(¬Pv¬Q))
Vom demonstra cea de-a doua dintre aceste teoreme. Aceasta este poate cea mai dificilă demonstrație pe care am văzut-o; ea necesită dovezi indirecte imbricate și o bună doză de inteligență în a găsi care va fi contradicția relevantă.

9.7 Utilizarea teoremelor
Care propoziție din logica noastră este, în termeni semantici, una din trei tipuri. Ea este fie o tautologie, fie o propoziție contradictorie, fie o propoziție contingentă. Am definit deja „tautologia” (o propoziție care trebuie să fie adevărată) și „propoziția contradictorie” (o propoziție care trebuie să fie falsă). O propoziție contingentă este o propoziție care nu este nici o tautologie, nici o propoziție contradictorie. Astfel, o propoziție contingentă este o propoziție care ar putea fi adevărată sau ar putea fi falsă.
Iată un exemplu pentru fiecare tip de propoziție:
(Pv¬P)
(P↔¬P)
P
P
Prima este o tautologie, a doua este o propoziție contradictorie, iar a treia este contingentă. Putem vedea acest lucru cu ajutorul unui tabel de adevăr.
| P | ¬P | (Pv¬P) | (P↔¬P) | P | |
| T | F | T | F | F | T |
| F | T | T | F | F | F |
Observați că negația unei tautologii este o contradicție, negația unei contradicții este o tautologie, iar negația unei propoziții contingente este o propoziție contingentă.
¬(Pv¬P)
¬(P↔¬P)
¬P
| P | ¬P | (Pv¬P) | ¬(Pv¬P) | ¬(Pv¬P) | (P↔¬P) | ¬(P↔¬P) | ||
| T | F | T | F | F | F | T | T | T |
| F | T | T | F | F | T | T |
Un moment de reflecție ne va arăta că ar fi un adevărat dezastru dacă fie o propoziție contradictorie, fie o propoziție contingentă ar fi o teoremă a logicii noastre propoziționale. Logica noastră a fost concepută pentru a produce numai argumente valide. Argumentele care nu au premise, am observat, ar trebui să aibă concluzii care trebuie să fie adevărate (din nou, acest lucru rezultă pentru că o propoziție care poate fi demonstrată fără premise ar putea fi demonstrată cu orice premise, și astfel ar fi bine să fie adevărată indiferent de premisele pe care le folosim). Dacă o teoremă ar fi contradictorie, am ști că am putea demonstra un fals. Dacă o teoremă ar fi contingentă, atunci, uneori, am putea demonstra un fals (adică am putea demonstra o propoziție care, în anumite condiții, este falsă). Și, având în vedere că am adoptat derivarea indirectă ca metodă de demonstrație, rezultă că, odată ce avem o contradicție sau o propoziție contradictorie într-un argument, putem demonstra orice.
Teoremele ne pot fi foarte utile în argumente. Să presupunem că știm că nici Smith și nici Jones nu vor merge la Londra și vrem să demonstrăm, prin urmare, că Jones nu va merge la Londra. Dacă ne-am permite să folosim una dintre teoremele lui De Morgan, am putea să rezolvăm rapid argumentul. Să presupunem următoarea cheie.
P: Smith va merge la Londra.
Q: Jones va merge la Londra.
Și avem următorul argument:
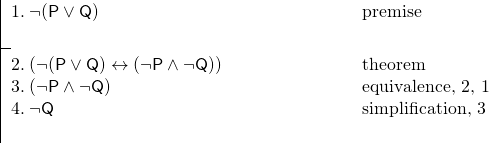
Această demonstrație a fost făcută foarte ușor prin utilizarea teoremei de la linia 2.
Există două lucruri de remarcat în legătură cu aceasta. În primul rând, ar trebui să ne permitem să facem acest lucru, deoarece dacă știm că o propoziție este o teoremă, atunci știm că am putea demonstra acea teoremă într-o subprobă. Adică, am putea înlocui linia 2 de mai sus cu o subprobă lungă care dovedește (¬(P v Q)↔(¬P ^ ¬Q))), pe care am putea apoi să o folosim. Dar dacă suntem siguri că (¬(P v Q)↔(¬P ^ ¬Q)) este o teoremă, nu ar trebui să fie nevoie să facem această dovadă din nou și din nou, de fiecare dată când dorim să folosim teorema.
A doua problemă pe care ar trebui să o recunoaștem este mai subtilă. Există infinit de multe propoziții de forma teoremei noastre, și ar trebui să le putem folosi și pe acestea. De exemplu, următoarele propoziții ar avea fiecare o demonstrație identică cu demonstrația teoremei noastre (¬(P v Q)↔(¬P ^ ¬Q)), cu excepția faptului că literele ar fi diferite:
(¬(R v S) ↔ (¬R ^ ¬S))
(¬(T v U) ↔ (¬T ^ ¬U))
(¬(V v W) ↔ (¬V ^ ¬W))
Să sperăm că acest lucru este evident. Luați dovada lui (¬(P v Q)↔(¬P ^ ¬Q)), și în acea dovadă înlocuiți fiecare instanță a lui P cu R și fiecare instanță a lui Q cu S, și veți avea o dovadă a lui (¬(R v S)↔(¬R ^ ¬S)).
Dar iată ceva care poate este mai puțin evident. Fiecare dintre cele ce urmează poate fi gândit ca fiind similar cu teorema (¬(P v Q)↔(¬P ^ ¬Q)).
(¬((P^Q) v (R^S))↔(¬(P^Q) ^ ¬(R^S)))
(¬(T v (Q v V))↔(¬T ^ ¬(Q v V))
(¬((Q↔P) v (¬R→¬Q))↔(¬(Q↔P) ^ ¬(¬R→¬Q)))
De exemplu:
, dacă se ia o dovadă de (¬(P v Q)↔(¬P ^ ¬Q)) și se înlocuiește fiecare instanță inițială a lui P cu (Q↔P) și fiecare instanță inițială a lui Q cu (¬R→¬Q), atunci s-ar obține o dovadă a teoremei (¬((Q↔P) v (¬R→¬Q))↔(¬(Q↔P) ^ ¬(¬R→¬Q)))).
Am putea surprinde această perspectivă în două moduri. Am putea enunța teoreme ale metalimbajului nostru și permite ca acestea să aibă instanțe. Astfel, am putea lua (¬(Φ v Ψ) ↔ (¬Φ ^ ¬Ψ))) ca o teoremă a metalimbajului, în care am putea înlocui fiecare Φ cu o propoziție și fiecare Ψ cu o propoziție și am putea obține o instanță particulară a unei teoreme. O alternativă este de a permite ca, pornind de la o teoremă, să putem produce alte teoreme prin substituire. Pentru ușurință, vom adopta această a doua strategie.
Regula noastră va fi următoarea. Odată ce am demonstrat o teoremă, o putem cita oricând într-o demonstrație. Justificarea noastră este că afirmația este o teoremă. Permitem înlocuirea oricărei propoziții atomice din teoremă cu orice altă propoziție dacă și numai dacă înlocuim fiecare instanță inițială a acelei propoziții atomice din teoremă cu aceeași propoziție.
Înainte de a considera un exemplu, este benefic să enumerăm câteva teoreme utile. Există infinit de multe teoreme ale limbii noastre, dar aceste zece sunt adesea foarte utile. Câteva dintre ele le-am demonstrat. Celelalte pot fi demonstrate ca un exercițiu.
T1 (P v ¬P)
T2 (¬(P→Q) ↔ (P^¬Q))
T3 (¬(P v Q) ↔ (¬P ^ ¬Q))
T4 ((¬P v ¬Q) ↔ ¬(P ^ Q))
T5 (¬(P ↔ Q) ↔ (P ↔ ¬Q))
T6 (¬P → (P → Q))
T7 (P → (Q → P))
T8 ((P→(Q→R)) → ((P→Q) → (P→R)))
T9 ((¬P→¬Q) → ((¬P→Q) →P))
T10 ((P→Q) → (¬Q→¬P))
Câteva exemple vor face clar avantajul utilizării teoremelor. Luați în considerare un argument diferit, pornind de la cel de mai sus. Știm că nu este cazul nici că dacă Smith merge la Londra, va merge la Berlin, nici că dacă Jones merge la Londra, va merge la Berlin. Dorim să demonstrăm că nu este cazul ca Jones să meargă la Berlin. Adăugăm la cheia noastră următoarele:
R: Smith va merge la Berlin.
S: Jones va merge la Berlin.
Și avem următorul argument:
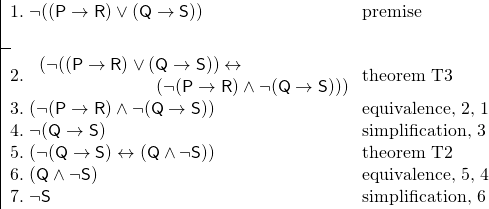
Utilizarea teoremelor a făcut ca această demonstrație să fie mult mai scurtă decât ar fi putut fi altfel. De asemenea, teoremele fac adesea ca o demonstrație să fie mai ușor de urmărit, deoarece recunoaștem teoremele ca tautologii – ca propoziții care trebuie să fie adevărate.
9.8 Probleme
- Demonstrați că fiecare dintre următoarele argumente este valid.
- Premise: P, ¬Q. Concluzie: ¬(P↔Q).
- Premise: (¬PvQ), (Pv¬Q). Concluzie: (P↔Q).
- Premise: (P↔Q), (R↔S) . Concluzia: ((P^R)↔(Q^S)).
- Dovadă fiecare dintre următoarele teoreme.
- T1
- T2
- T5
- T6
- T7
- T8
- T9
- T9
- ((P^Q)↔¬(¬Pv¬Q))).
- ((P→Q)↔¬(P^¬Q))
- În engleză colocvială normală, scrieți propriul argument valid cu cel puțin două premise, dintre care cel puțin una este bicondițională. Argumentul tău trebuie să fie doar un paragraf (nu o listă ordonată de propoziții sau orice altceva care să semene cu logica formală). Traduceți-l în logica propozițională și dovediți că este valid.
- În engleză colocvială normală, scrieți propriul argument valid cu cel puțin două premise și cu o concluzie care să fie bicondițională. Argumentul tău ar trebui să fie doar un paragraf (nu o listă ordonată de propoziții sau orice altceva care să arate formal ca o logică). Traduceți-l în logica propozițională și dovediți că este valid.
Din Enquiry Concerning Human Understanding a lui Hume, p.161 în Selby-Bigge și Nidditch (1995 ).