
Întrebarea de politică: Creditul fiscal pentru achiziționarea de mașini hibride – Este cea mai bună alegere a guvernului pentru a reduce consumul de combustibil și emisiile de carbon?
Locuitorii SUA și guvernul sunt îngrijorați de dependența de petrolul străin importat și de eliberarea de carbon în atmosferă. În 2005, Congresul a adoptat o lege pentru a oferi consumatorilor credite fiscale pentru achiziționarea de autovehicule electrice și hibride.
Acest credit fiscal poate părea o alegere politică bună, dar este costisitor, deoarece scade în mod direct valoarea veniturilor pe care le colectează guvernul SUA. Există abordări mai eficiente pentru reducerea dependenței de combustibilii fosili și a emisiilor de carbon? Cum putem decide care este cea mai bună politică? Pentru a răspunde la această întrebare, factorii de decizie politică trebuie să prevadă cu o anumită acuratețe modul în care consumatorii vor reacționa la această politică fiscală înainte ca acești factori de decizie politică să cheltuiască milioane de dolari federali.
Putem aplica conceptul de utilitate la această întrebare politică. În acest modul, vom studia utilitatea și funcțiile de utilitate. Vom putea apoi să folosim o funcție de utilitate adecvată pentru a deriva curbele de indiferență care descriu întrebarea noastră de politică.
Explorarea întrebării de politică
Să presupunem că creditul fiscal pentru subvenționarea achizițiilor de mașini hibride are un succes nebunesc și dublează economia medie de combustibil a tuturor mașinilor de pe drumurile din SUA – un rezultat care în mod clar nu este realist, dar care este util pentru discuțiile noastre ulterioare. Ce credeți că s-ar întâmpla cu consumul de combustibil al tuturor automobiliștilor din SUA? Ar trebui ca guvernul să se aștepte ca, drept răspuns, consumul de combustibil și emisiile de carbon ale automobilelor să scadă la jumătate? De ce sau de ce nu?
2.1 Funcții de utilitate
LO 2.1: Descrieți o funcție de utilitate.
2.2 Funcții de utilitate și preferințe tipice
LO 2.2: Identificați funcțiile de utilitate pe baza preferințelor tipice pe care le reprezintă.
2.3 Relaționarea funcțiilor de utilitate și a hărților curbelor de indiferență
LO 2.3: Explicați cum să derivați o curbă de indiferență dintr-o funcție de utilitate.
2.4 Găsirea utilității marginale și a ratei marginale de substituție
LO 2.4: Derivați utilitatea marginală și RMS pentru funcții de utilitate tipice.
2.5. Întrebare de politică
2.1 Funcții de utilitate
LO1: Descrieți o funcție de utilitate.
Preferințele noastre ne permit să facem comparații între diferite pachete de consum și să alegem pachetele preferate. Am putea, de exemplu, să determinăm ordinea de rang a unui întreg set de pachete pe baza preferințelor noastre. O funcție de utilitate este o funcție matematică care clasifică pachetele de bunuri de consum prin atribuirea unui număr pentru fiecare dintre ele, unde numerele mai mari indică pachetele preferate. Funcțiile de utilitate au proprietățile pe care le-am identificat în modulul 1 cu privire la preferințe. Adică: sunt capabile să ordoneze pachete, sunt complete și tranzitive, mai mult este preferat mai mult decât mai puțin și, în cazuri relevante, pachetele mixte sunt mai bune.
Numărul pe care funcția de utilitate îl atribuie unui anumit pachet este cunoscut sub numele de utilitate, adică satisfacția pe care un consumator o obține de la un anumit pachet. Numărul de utilitate pentru fiecare pachet nu înseamnă nimic în termeni absoluți; nu există o scală uniformă în raport cu care să măsurăm satisfacția. Singurul său scop este în termeni relativi: putem folosi utilitatea pentru a determina ce pachete sunt preferate față de altele.
Dacă utilitatea din pachetul A este mai mare decât utilitatea din pachetul B, este echivalent cu a spune că un consumator preferă pachetul A în locul pachetului B. Prin urmare, funcțiile de utilitate clasifică preferințele consumatorilor prin atribuirea unui număr fiecărui pachet. . Putem utiliza o funcție de utilitate pentru a trasa hărțile curbelor de indiferență descrise în modulul 1. Deoarece toate pachetele de pe aceeași curbă de indiferență oferă aceeași satisfacție și, prin urmare, niciunul nu este preferat, fiecare pachet are aceeași utilitate. Prin urmare, putem trasa o curbă de indiferență prin determinarea tuturor pachetelor care returnează același număr din funcția de utilitate.
Economiștii spun că funcțiile de utilitate sunt mai degrabă ordinale decât cardinale. Ordinal înseamnă că funcțiile de utilitate clasifică doar pachetele – ele indică doar care dintre ele este mai bun, nu cu cât este mai bun decât un alt pachet. Să presupunem, de exemplu, că o funcție de utilitate indică faptul că pachetul A returnează 10 utilități și pachetul B 20 de utilități. Nu spunem că pachetul B este de două ori mai bun sau 10 utilități mai bun, ci doar că consumatorul preferă pachetul B. De exemplu, să presupunem că o prietenă s-a înscris la o cursă și v-a spus că s-a clasat pe locul al treilea. Această informație este ordinală: Știți că a fost mai rapidă decât a patra clasată și mai lentă decât a doua clasată. Știți doar ordinea în care au terminat alergătorii. Timpii individuali sunt cardinale: Dacă primul clasat a alergat în exact o oră, iar prietenul dvs. a terminat cursa într-o oră și șase minute, știți că prietenul dvs. a fost cu exact 10% mai lent decât cel mai rapid alergător. deoarece funcțiile de utilitate sunt ordinale, multe funcții de utilitate diferite pot reprezenta aceleași preferințe. Acest lucru este adevărat atâta timp cât se păstrează ordinea.
Să luăm de exemplu funcția de utilitate U care descrie preferințele asupra pachetelor de bunuri A și B: U(A,B). Putem aplica orice transformare monotonică pozitivă acestei funcții (ceea ce înseamnă, în esență, că nu schimbăm ordinea) și noua funcție pe care am creat-o va reprezenta aceleași preferințe. De exemplu, am putea înmulți o constantă pozitivă, α , sau adăuga o constantă pozitivă sau negativă, β . Așadar, αU(A,B)+β reprezintă exact aceleași preferințe ca și U(A,B), deoarece va ordona pachetele în exact același mod. Acest fapt este destul de util deoarece, uneori, aplicarea unei transformări monotonice pozitive a unei funcții de utilitate facilitează rezolvarea problemelor.
2.2 Funcții de utilitate și preferințe tipice
LO2: Identificați funcțiile de utilitate pe baza preferințelor tipice pe care le reprezintă
Considerați pachetele de mere, A, și de banane, B. O funcție de utilitate care descrie preferințele lui Isaac pentru pachetele de mere și banane este funcția U(A,B). Dar care sunt preferințele particulare ale lui Isaac pentru pachetele de mere și banane? Să presupunem că Isaac are preferințe destul de standard pentru mere și banane, care conduc la curbele noastre tipice de indiferență: El preferă mai mult decât mai puțin și îi place varietatea. O funcție de utilitate care să reprezinte aceste preferințe ar putea fi:
U(A,B) = AB
Dacă merele și bananele sunt completări perfecte în preferințele lui Isaac, funcția de utilitate ar arăta cam așa:
U(A,B) = MIN,
unde funcția MIN atribuie pur și simplu cel mai mic dintre cele două numere ca valoare a funcției.
Dacă merele și bananele sunt înlocuitori perfecți, funcția de utilitate este aditivă și ar arăta cam așa:
U(A,B) = A + B
O clasă de funcții de utilitate cunoscute sub numele de funcții de utilitate Cobb-Douglas sunt foarte frecvent utilizate în economie din două motive:
1. Ele reprezintă preferințe „bine comportate”, cum ar fi „mai mult este mai bine” și preferința pentru varietate.
2. Ele sunt foarte flexibile și pot fi ajustate foarte ușor pentru a se potrivi datelor din lumea reală.
Funcțiile de utilitate Cobb-Douglas au această formă:
U(A,B) = AαBβ
Pentru că transformările monotonice pozitive reprezintă aceleași preferințe, o astfel de transformare poate fi folosită pentru a seta α + β = 1 , ceea ce mai târziu vom vedea că este o condiție convenabilă care simplifică unele calcule matematice în problema alegerii consumatorului.
O altă modalitate de a transforma funcția de utilitate într-un mod util este de a lua logaritmul natural al funcției, ceea ce creează o nouă funcție care arată astfel:
U(A,B) = αln(A) + βln(B)
Pentru a obține această ecuație, pur și simplu se aplică regulile logaritmilor naturali . Este important să se țină cont de nivelul de abstractizare de aici. De obicei, nu putem realiza funcții de utilitate specifice care să descrie cu precizie preferințele individuale. Probabil că niciunul dintre noi nu și-ar putea descrie propriile preferințe cu o singură ecuație. Dar, atâta timp cât consumatorii în general au preferințe care respectă ipotezele noastre de bază, putem face o treabă destul de bună pentru a găsi funcții de utilitate care să corespundă datelor de consum din lumea reală. Vom vedea dovezi în acest sens mai târziu în cursul nostru.
Tabelul 2.1 rezumă preferințele și funcțiile de utilitate descrise în această secțiune.
|
Tabelul 2.1 Tipuri de preferințe și funcțiile de utilitate care le reprezintă |
||
|
PREFERINȚE |
UTILITATE FUNCȚIE |
TIP DE FUNCȚIE UTILITARĂ |
|
Iubire de varietate sau „bine crescută” |
U(A,B) = AB |
Cobb-Douglas |
|
Love of Variety or „Well Behaved” |
U(A,B) = AαBβ |
Cobb-Douglas |
|
Love of Variety or „Well Behaved” |
U(A,B) = αln(A) + βln(B) |
Log natural Cobb-Douglas |
|
Complemente perfecte |
U(A,B) = MIN |
Funcția Min |
|
Înlocuitori perfecți |
U(A,B) = A + B |
Additiv |
2.3 Relaționarea funcțiilor de utilitate și a hărților curbelor de indiferență
LO3: Explicarea modului în care se obține o curbă de indiferență dintr-o funcție de utilitate
Curbele de indiferență și funcțiile de utilitate sunt direct legate. De fapt, din moment ce curbele de indiferență reprezintă preferințele grafic, iar funcțiile de utilitate reprezintă preferințele matematic, rezultă că curbele de indiferență pot fi derivate din funcțiile de utilitate.
În funcțiile uni-variate, variabila dependentă este reprezentată pe axa verticală, iar variabila independentă este reprezentată pe axa orizontală, precum graficul lui y=f(x). În schimb, graficele funcțiilor bi-variate sunt tridimensionale, cum ar fi U=U(A,B). Figura 2.1 prezintă un grafic al lui U=A^\frac{1}{2}B^frac{1}{2}. Graficele tridimensionale sunt utile pentru a înțelege modul în care utilitatea crește odată cu creșterea consumului atât de A, cât și de B.
Figura 2.1 U=A^\frac{1}{2}B^\frac{1}{2}
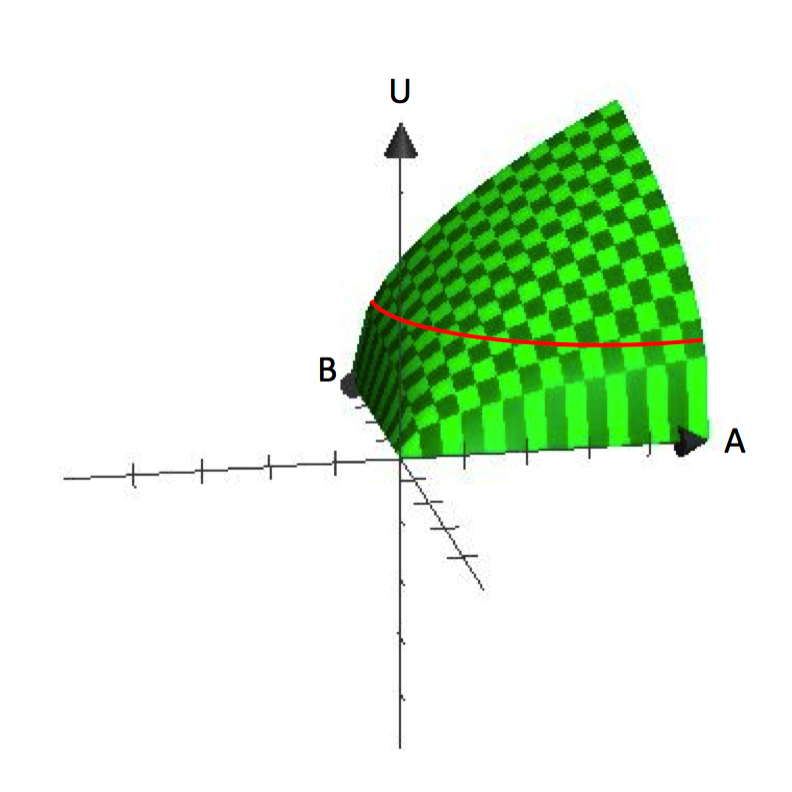
Figura 2.1 arată clar ipoteza că consumatorii au o preferință pentru varietate. Fiecare pachet care conține o anumită cantitate de A și B reprezintă un punct de pe suprafață. Înălțimea verticală a suprafeței reprezintă nivelul de utilitate. Prin creșterea atât a lui A, cât și a lui B, un consumator poate atinge puncte mai înalte pe suprafață.
Atunci de unde vin curbele de indiferență? Reamintim că o curbă de indiferență este o colecție a tuturor pachetelor care îi sunt indiferente unui consumator, în ceea ce privește pe care să le consume. Din punct de vedere matematic, acest lucru este echivalent cu a spune că toate pachetele, atunci când sunt puse în funcția de utilitate, returnează aceeași valoare funcțională. Așadar, dacă stabilim o valoare pentru utilitate, Ū, și găsim toate pachetele A și B care generează această valoare, vom defini o curbă de indiferență. Observați că acest lucru este echivalent cu găsirea tuturor pachetelor care îl duc pe consumator la aceeași înălțime pe suprafața tridimensională din figura 2.1.
Curbele de indiferență sunt o reprezentare a înălțimii (nivelului de utilitate) pe o suprafață plană. În acest fel, ele sunt analoage cu o curbă de nivel pe o hartă topografică. Prin readucerea graficului tridimensional în spațiul bidimensional – spațiul A, B – putem arăta liniile de contur/curbele de diferență care reprezintă diferite înălțimi sau niveluri de utilitate. Din graficul din figura 2.1, puteți vedea deja cum această funcție de utilitate produce curbe de indiferență care sunt „arcuite” sau concave față de origine.
Deci, curbele de indiferență decurg direct din funcțiile de utilitate și sunt o modalitate utilă de a reprezenta funcțiile de utilitate într-un grafic bidimensional.
2.4 Găsirea utilității marginale și a ratei marginale de substituție
LO4: Să se deducă utilitatea marginală și RMS pentru funcții de utilitate tipice.
Utilitatea marginală este utilitatea suplimentară pe care o primește un consumator dacă consumă o unitate suplimentară dintr-un bun. Din punct de vedere matematic, o exprimăm astfel:
MU_{a}=\frac{\Delta \cup }{\Delta A}
sau variația utilității ca urmare a unei modificări a cantității de A consumate, unde Δ reprezintă o modificare a valorii bunului. Așadar,
MU_{a}=\frac{\Delta \cup }{\Delta A}=\frac{\cup (A+\Delta A,B)-U(A,B)}{\Delta A}
Rețineți că, atunci când examinăm utilitatea marginală a consumului lui A, menținem B constant.
Utilizând calculul, utilitatea marginală este aceeași cu derivata parțială a funcției de utilitate în raport cu A:
MU_{A}\frac{\partial U(A,B)}{\partial A}
Considerăm un consumator care se așează să mănânce o masă de salată și pizza. Să presupunem că menținem constantă cantitatea de salată – o salată de garnitură la o cină, de exemplu. Acum să creștem numărul de felii de pizza presupunem că cu 1 felie utilitatea este de 10, cu 2 este de 18, cu 3 este de 24 și cu 4 este de 28. Să reprezentăm aceste numere pe un grafic care are utilitatea pe axa verticală și pizza pe axa orizontală (figura 2.2).
Figura 2.2: Graficul și tabelul utilității marginale descrescătoare
|
Pizza felii |
Utilitate |
Utilitate |
Marginală Utilități |
|
1 |
10 |
|
|
|
2 |
18 |
8 |
|
|
3 |
24 |
6 |
|
|
4 |
28 |
4 |
|
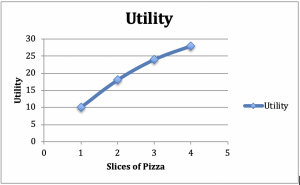
Din panta pozitivă a graficului, putem observa creșterea utilității din cauza feliilor suplimentare de pizza. Din forma concavă a graficului, putem observa un alt fenomen comun: Utilitatea suplimentară pe care consumatorul o primește de la fiecare felie suplimentară de pizza scade odată cu numărul de felii consumate.
Faptul că utilitatea suplimentară devine mai mică cu fiecare felie suplimentară de pizza se numește principiul utilității marginale descrescătoare. Acest principiu se aplică preferințelor bine comportate în care sunt preferate pachetele mixte.
Rata marginală de substituție (MRS) este cantitatea dintr-un bun la care un consumator este dispus să renunțe pentru a obține încă o unitate dintr-un alt bun. Acesta este motivul pentru care este același lucru cu panta curbei de indiferență – din moment ce menținem constant nivelul de satisfacție, rămânem pe aceeași curbă de indiferență, doar că ne deplasăm de-a lungul ei pe măsură ce schimbăm un bun pentru altul. Cât de mult din unul sunteți dispus să schimbați pentru încă unul din altul depinde de utilitatea marginală de la fiecare.
Utilizând exemplul nostru anterior, dacă consumând încă o salată laterală utilitatea dumneavoastră crește cu 10, atunci la un consum actual de 4 felii de pizza, ați putea renunța la 2 felii de pizza și ați putea trece de la 28 la 18 utilități. 10 utilități în plus de la salată și 10 utilități în minus prin renunțarea la 2 felii de pizza lasă utilitatea generală neschimbată – deci trebuie să ne aflăm în continuare pe aceeași curbă de indiferență. Pe măsură ce vă deplasați de-a lungul curbei de indiferență, trebuie să vă deplasați pe pantă, adică trebuie să renunțați la bunul de pe axa verticală pentru mai mult bun pe axa orizontală, ceea ce produce o creștere negativă pe o cursă pozitivă.
Potem trece direct de la utilitatea marginală la MRS recunoscând legătura dintre cele două concepte. În cazul nostru, pentru o funcție de utilitate U=U(A,B) , MRS se reprezintă astfel:
MRS=-\frac{MU_{A}}{MU_{B}}
Rețineți că atunci când înlocuim putem simplifica ecuația:
MRS=-\frac{MU_{A}}}{MU_{B}}=-\frac{\frac{\Delta U}{\Delta A}}{\frac{\Delta U}{\Delta B}}=-\frac{\Delta B}{\Delta A}
Inserând calculul, aceasta echivalează cu:
MRS=-\frac{\frac{\parțial U(A,B)}{\parțial A}}{\frac{\parțial U(A,B)}{\parțial B}}
2.5 Întrebare de politică
Am stabilit în modulul 1 că decizia relevantă a consumatorului între mai mulți kilometri parcurși și alte tipuri de consum este probabil conformă cu ipotezele standard privind alegerea consumatorului. Prin urmare, utilizarea funcției de utilitate Cobb-Douglas pentru a reprezenta un consumator căruia îi place să conducă o mașină, precum și să consume alte bunuri, și care le vede ca pe un compromis (banii cheltuiți pe benzină sunt bani care nu sunt cheltuiți pe alte bunuri de consum), este o alegere bună. De asemenea, are avantajul de a fi atât conformă cu ipotezele, cât și flexibilă:
U(MD,C)=MD^{a}C^{\beta } ,
unde MD = Milele parcurse, iar C = Alt consum.
De fapt, funcția însăși poate fi dusă la date din lumea reală, unde parametrii și pot fi estimați pentru această piață, piața kilometrilor parcurși în mașina consumatorului.
Figura 2.3 Graficul curbelor de indiferență pentru exemplul de politică
Explorarea întrebărilor de politică:
1 . Ar fi alte tipuri de preferințe mai adecvate în acest exemplu?
2. Ce ar trebui să fie adevărat pentru ca complementele perfecte să fie tipul de preferință adecvat de utilizat pentru a analiza această politică?
Ce ar trebui să fie adevărat pentru înlocuitorii perfecți? 3. Având în vedere că avem în vedere un consumator „tipic” care conduce, este adecvat să alegem o funcție de utilitate „tipică”?
4. Suntem doar niște presupuneri sau avem o bază teoretică pentru a susține alegerea preferințelor „bine comportate” sau a unei funcții de utilitate Cobb-Douglas?
REZUMAT
Revizuire: Subiecte și rezultate ale învățării aferente
2.1 Funcții de utilitate
LO 2.1: Descrieți o funcție de utilitate
2.2 Funcții de utilitate și preferințe tipice
LO 2.2: Identificați funcțiile de utilitate pe baza preferințelor tipice pe care le reprezintă
LO 2.3 Relaționarea funcțiilor de utilitate și a hărților curbelor de indiferență
LO 2.3: Explicați cum să derivați o curbă de indiferență dintr-o funcție de utilitate
LO 2.4 Găsirea utilității marginale și a ratei marginale de substituție
LO 2.4: Deduceți utilitatea marginală și RMS pentru funcții de utilitate tipice.
LO 2.5: Explicați cum să obțineți utilitatea marginală și RMS pentru funcții de utilitate tipice. Întrebare de politică
Învățați: Termeni cheie și grafice
Bi-funcții variate
Cardinal
Linia de contur
Utilitate marginală descrescătoare
Funcție
Rata marginală de substituție (MRS)
Utilitate marginală
.
Funcții ordonate
Funcții univariate
Utilități
Utilitate
Funcție de utilitate
Grafice
Funcție de utilitate 3D și curbă de nivel
Equații
Cobb-Douglas
Complemente perfecte
Înlocuitori perfecți
.