
Savantul grec clasic Aristotel (384-322 î.Hr.) a fost primul care a acordat o atenție serioasă curcubeului. Potrivit lui Raymond L. Lee și Alistair B. Fraser: „În ciuda numeroaselor sale defecte și a apelului său la numerologia pitagoreică, explicația calitativă a lui Aristotel a dat dovadă de o inventivitate și de o coerență relativă care nu a mai fost egalată timp de secole. După moartea lui Aristotel, o mare parte din teoretizarea curcubeului a constat în reacții la opera sa, deși nu toate au fost lipsite de critică.”
În Cartea I din Naturales Quaestiones (c. 65 d.Hr.), filozoful roman Seneca cel Tânăr discută pe larg diverse teorii ale formării curcubeului, inclusiv pe cele ale lui Aristotel. El observă că curcubeele apar întotdeauna vizavi de soare, că apar în apa pulverizată de un vâslaș, în apa scuipată de un bici pe haine întinse cu cleștele sau în apa pulverizată printr-o gaură mică dintr-o țeavă spartă. El a vorbit chiar despre curcubeele produse de mici tije de sticlă (virgulae), anticipând experimentele lui Newton cu prisme. Avea în minte două teorii: una, conform căreia curcubeul era produs de soarele care reflecta fiecare picătură de apă, iar cealaltă, conform căreia era produs de soarele care reflecta un nor sub forma unei oglinzi concave; a preferat-o pe cea din urmă. El a discutat și despre alte fenomene legate de curcubeu: misterioasele „virgas” (tije), halourile și parheliile.
Potrivit lui Hüseyin Gazi Topdemir, fizicianul și politologul arab Ibn al-Haytham (Alhazen; 965-1039), a încercat să ofere o explicație științifică pentru fenomenul curcubeului. În lucrarea sa Maqala fi al-Hala wa Qaws Quzah , al-Haytham „a explicat formarea curcubeului ca pe o imagine, care se formează într-o oglindă concavă. Dacă razele de lumină care vin de la o sursă de lumină mai îndepărtată se reflectă în orice punct de pe axa oglinzii concave, ele formează cercuri concentrice în acel punct. Dacă se consideră că soarele este o sursă de lumină suplimentară, ochiul privitorului este un punct pe axa oglinzii și un nor este o suprafață reflectantă, atunci se poate observa că se formează cercuri concentrice pe axă”. El nu a putut verifica acest lucru deoarece teoria sa conform căreia „lumina soarelui este reflectată de un nor înainte de a ajunge la ochi” nu permitea o posibilă verificare experimentală. Această explicație a fost repetată de Averroes și, deși incorectă, a stat la baza explicațiilor corecte oferite mai târziu de Kamāl al-Dīn al-Fārisī în 1309 și, independent, de Theodoric din Freiberg (cca. 1250 – cca. 1311) – ambii studiaseră Cartea de optică a lui al-Haytham.
Un contemporan al lui Ibn al-Haytham, filosoful și savantul persan Ibn Sīnā (Avicenna, 980-1037), a oferit o explicație alternativă: „că arcul nu se formează în norul întunecat, ci mai degrabă în ceața foarte fină care se află între nor și soare sau observator. Norul, a crezut el, servește doar ca un fundal pentru această substanță subțire, la fel ca atunci când un strat de mercur este plasat pe suprafața din spate a sticlei unei oglinzi. Ibn Sīnā ar muta locul nu numai al arcului, ci și al formării culorii, susținând că irizația este pur și simplu o senzație subiectivă a ochiului”. Cu toate acestea, această explicație era, de asemenea, incorectă. Relatarea lui Ibn Sīnā a acceptat multe dintre argumentele lui Aristotel despre curcubeu.
În China din dinastia Song (960-1279), un polimat și erudit oficial pe nume Shen Kuo (1031-1095) a emis ipoteza – așa cum făcuse anterior un anume Sun Sikong (1015-1076) – că curcubeul se formează printr-un fenomen de întâlnire a luminii solare cu picăturile de ploaie din aer. Paul Dong subliniază că explicația lui Shen despre curcubeu ca fiind un fenomen de refracție atmosferică „este în principiu în conformitate cu principiile științifice moderne”.
Potrivit lui Nader El-Bizri, astronomul persan Qutb al-Din al-Shirazi (1236-1311), a dat o explicație destul de precisă a fenomenului curcubeului. Aceasta a fost dezvoltată de elevul său, Kamāl al-Dīn al-Fārisī (1267-1319), care a oferit o explicație mai satisfăcătoare din punct de vedere matematic a curcubeului. „El a propus un model în care raza de lumină de la soare era refractată de două ori de o picătură de apă, una sau mai multe reflexii având loc între cele două refracții.” A fost efectuat un experiment cu o sferă de sticlă umplută cu apă și al-Farisi a arătat că refracțiile suplimentare datorate sticlei pot fi ignorate în modelul său. După cum se menționează în lucrarea sa Kitab Tanqih al-Manazir , al-Farisi a folosit un vas mare de sticlă transparentă în formă de sferă, care a fost umplut cu apă, pentru a avea un model experimental la scară mare al unei picături de ploaie. Apoi a plasat acest model într-o cameră întunecată care avea o deschidere controlată pentru a permite trecerea luminii. El a proiectat lumina pe sferă și, în cele din urmă, a dedus, prin diverse teste și observații detaliate ale reflexiilor și refracțiilor luminii, că culorile curcubeului sunt fenomene de degradare a luminii.
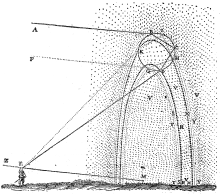
În Europa, Cartea de optică a lui Ibn al-Haytham a fost tradusă în latină și studiată de Robert Grosseteste. Lucrările sale asupra luminii au fost continuate de Roger Bacon, care a scris în lucrarea sa Opus Majus din 1268 despre experimentele cu lumina care strălucește prin cristale și picături de apă și care arată culorile curcubeului. În plus, Bacon a fost primul care a calculat dimensiunea unghiulară a curcubeului. El a precizat că vârful curcubeului nu poate apărea la mai mult de 42° deasupra orizontului. Se știe că Theodoric din Freiberg a oferit o explicație teoretică precisă atât a curcubeelor primare, cât și a celor secundare în 1307 (dezvoltată ulterior de Antonius din Demini în 1611). El a explicat curcubeul primar, observând că „atunci când lumina soarelui cade pe picături individuale de umezeală, razele suferă două refracții (la intrare și la ieșire) și o reflexie (în spatele picăturii) înainte de a fi transmise către ochiul observatorului”. El a explicat curcubeul secundar printr-o analiză similară care implică două refracții și două reflexii.
René Descartes, în tratatul său din 1637, Discurs despre metodă, a avansat și mai mult această explicație. Știind că mărimea picăturilor de ploaie nu pare să afecteze curcubeul observat, a experimentat trecerea razelor de lumină printr-o sferă mare de sticlă umplută cu apă. Măsurând unghiurile la care au apărut razele, a ajuns la concluzia că arcul primar a fost cauzat de o singură reflexie internă în interiorul picăturii de ploaie și că arcul secundar ar putea fi cauzat de două reflexii interne. El a susținut această concluzie cu o derivare a legii refracției (ulterioară, dar independentă de legea lui Snell) și a calculat corect unghiurile pentru ambele arce. Cu toate acestea, explicația sa privind culorile se baza pe o versiune mecanică a teoriei tradiționale conform căreia culorile erau produse printr-o modificare a luminii albe.
Isaac Newton a demonstrat că lumina albă era compusă din lumina tuturor culorilor curcubeului, pe care o prismă de sticlă o putea separa în întregul spectru de culori – descompunerea luminii albe – respingând teoria conform căreia culorile erau produse printr-o modificare a luminii albe. El a arătat, de asemenea, că lumina roșie se refractă mai puțin decât cea albastră, ceea ce a condus la prima explicație științifică a principalelor caracteristici ale curcubeului. Teoria corpusculară a luminii a lui Newton nu a fost capabilă să explice curcubeele supranumerare, pentru care nu s-a găsit nicio explicație satisfăcătoare până când Thomas Young și-a dat seama că lumina se comportă ca o undă în anumite condiții și că poate interfera cu ea însăși.
Lucrarea lui Young, elaborată ulterior în detaliu de Richard Potter, a fost rafinată în anii 1820 de George Biddell Airy, care a explicat că există o dependență între intensitatea culorilor curcubeului și mărimea picăturilor de apă. Descrierile fizice moderne ale curcubeului se bazează pe dispersia Mie, publicată de Gustav Mie în 1908. Progresele în metodele de calcul și în teoria optică continuă să ducă la o înțelegere mai completă a curcubeului. De exemplu, Nussenzveig oferă o privire de ansamblu modernă.

.