În această lecție, vom arăta o strategie ușoară pentru rezolvarea următoarei probleme: cum să găsim aria unui triunghi isoscel.
Să punem în practică o serie de proprietăți pe care le-am demonstrat până acum, în următoarea problemă de geometrie:
Problemă
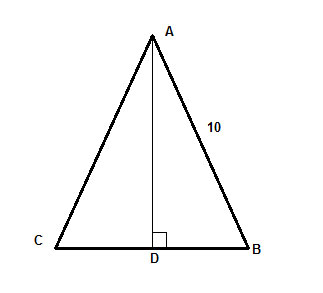
Într-un triunghi isoscel, ΔABC, cu lungimea catetei 10, înălțimea la bază este egală cu două treimi din bază. Găsiți aria triunghiului.
Strategie
Pentru a rezolva această problemă, Vom lucra invers față de ceea ce trebuie să facem.
Trebuie să găsim aria triunghiului, care știm că este dată de formula (baza înmulțită cu înălțimea)/2.
O problemă pe care o avem este că nu cunoaștem nici lungimea bazei, nici înălțimea. Dar, ni se dă relația dintre ele, care este indiciul a ceea ce trebuie să facem. Să numim lungimea bazei, BC, x.
Apoi știm că înălțimea, AD, este 2x/3, așa cum este dat în problemă.
Atunci răspunsul pe care îl căutăm este (baza ori înălțimea)/2, sau x ori 2x/3, împărțit la doi.
Dar cum găsim x? Există două lucruri suplimentare care ne-au fost date în problemă și pe care nu le-am folosit încă – lungimea piciorului (10) și faptul că acesta este un triunghi isoscel. Probabil că trebuie să folosim aceste două lucruri pentru a rezolva problema.
Să recapitulăm proprietățile triunghiurilor isoscele. Un lucru care ar trebui să ne sară imediat în minte este că, așa cum am arătat, într-un triunghi isoscel, înălțimea până la bază bisectează baza, deci CD=DB=x/2.
În cele din urmă, AD este înălțimea, ceea ce înseamnă că unghiul ∠ADC este un unghi dreptunghic și avem un triunghi dreptunghic, ΔADC, a cărui ipotenuză o cunoaștem (10) și o putem folosi pentru a găsi catetele folosind teorema lui Pitagora, c2 =a2+b2,
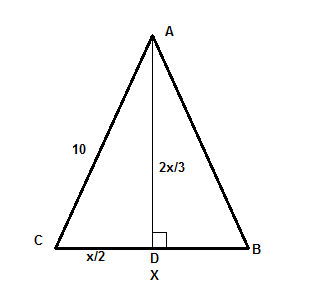
unde c= 10 ,a = x/2 și b=2x/3 . Și am terminat, restul este doar rezolvarea algebrică a lui x.
Probă: aria unui triunghi isoscel
(1) ΔADC este triunghi dreptunghic //datorită, deoarece AD este înălțimea până la bază
(2) AC2 =CD2 + AD2 //Teorema lui Pitagora
(3) AC= 10 //datorită
(4) CB = x
(5) CD = x/2 //înălțimea până la bază în triunghiul isoscel intersectează baza
(6) AD = 2x/3 //datorită
(7) 102 = (x/2)2 + (2x/3)2 //Substituie în (2)
(8) 100 = x2/4+4×2/9 //simplifică
(9) 100*36 = 9×2 +16×2 //multiplică ambele părți cu 36
(10) 100*36 = 25×2 //colectează termenii similari
.