Ecartul standard este valoarea medie a variabilității din setul de date. Ea vă spune, în medie, cât de departe se află fiecare valoare de medie.
O abatere standard mare înseamnă că valorile sunt, în general, departe de medie, în timp ce o abatere standard mică indică faptul că valorile sunt grupate aproape de medie.
Ce vă spune abaterea standard?
Deviația standard este o măsură utilă de răspândire pentru distribuțiile normale.
În distribuțiile normale, datele sunt distribuite simetric, fără distorsiuni. Cele mai multe valori se grupează în jurul unei regiuni centrale, valorile scăzând pe măsură ce se îndepărtează de centru. Abaterea standard vă spune cât de depărtate de centrul distribuției sunt, în medie, datele dumneavoastră.
Multe variabile științifice urmează distribuții normale, inclusiv înălțimea, notele la testele standardizate sau ratingurile de satisfacție la locul de muncă. Atunci când aveți abaterile standard ale unor eșantioane diferite, puteți compara distribuțiile lor folosind teste statistice pentru a face deducții despre populațiile mai mari din care provin.
Evaluările medii (M) sunt aceleași pentru fiecare grup – este valoarea de pe axa x atunci când curba este la vârf. Cu toate acestea, deviațiile lor standard (SD) diferă una de cealaltă.
Deviația standard reflectă dispersia distribuției. Curba cu cea mai mică abatere standard are un vârf ridicat și o dispersie mică, în timp ce curba cu cea mai mare abatere standard este mai plată și mai răspândită.
Regula empirică
Deviația standard și media împreună vă pot spune unde se află cele mai multe dintre valorile din distribuția dvs. dacă acestea urmează o distribuție normală.
Regula empirică, sau regula 68-95-99,7, vă spune unde se află valorile dvs.:
- În jur de 68% din scoruri se situează în limita a 2 abateri standard de la medie,
- În jur de 95% din scoruri se situează în limita a 4 abateri standard de la medie,
- În jur de 99.7% din scoruri se încadrează în 6 deviații standard de la medie.
Să urmăm regula empirică:
- Aproximativ 68% din scoruri sunt cuprinse între 40 și 60.
- Aproximativ 95% din scoruri sunt cuprinse între 30 și 70.
- În jur de 99,7% din scoruri sunt cuprinse între 20 și 80.
Regula empirică este o modalitate rapidă de a obține o imagine de ansamblu a datelor dvs. și de a verifica dacă există valori aberante sau extreme care nu respectă acest model.
Pentru distribuțiile non-normale, abaterea standard este o măsură mai puțin fiabilă a variabilității și ar trebui utilizată în combinație cu alte măsuri, cum ar fi intervalul sau intervalul interquartil.
Formule de calcul al abaterii standard pentru populații și eșantioane
Pentru calcularea abaterilor standard se folosesc formule diferite, în funcție de faptul că aveți date de la o populație întreagă sau de la un eșantion.
Ecartul standard al populației
Când ați colectat date de la fiecare membru al populației care vă interesează, puteți obține o valoare exactă pentru abaterea standard a populației.
Formula abaterii standard a populației arată astfel:
| Formula | Explicație |
|---|---|
 |
|
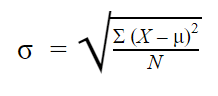Deviația standard a eșantionului
Când se colectează date dintr-un eșantion, deviația standard a eșantionului este folosită pentru a face estimări sau inferențe despre deviația standard a populației.
Formula abaterii standard a eșantionului arată astfel:
| Formula | Explicație |
|---|---|
 |
|
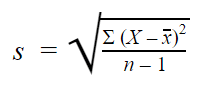În cazul eșantioanelor, folosim n – 1 în formulă, deoarece folosirea lui n ne-ar da o estimare distorsionată care subestimează în mod constant variabilitatea. Abaterea standard a eșantionului ar tinde să fie mai mică decât abaterea standard reală a populației.
Reducând eșantionul n la n – 1, abaterea standard devine artificial de mare, dându-vă o estimare conservatoare a variabilității.
În timp ce aceasta nu este o estimare nepărtinitoare, este o estimare mai puțin părtinitoare a deviației standard: este mai bine să supraestimezi decât să subestimezi variabilitatea în eșantioane.
Pași pentru calcularea abaterii standard
Deviația standard este, de obicei, calculată automat de către orice software pe care îl folosiți pentru analiza statistică. Dar o puteți calcula și manual pentru a înțelege mai bine cum funcționează formula.
Există șase pași principali pentru a găsi abaterea standard manual. Vom folosi un mic set de date de 6 scoruri pentru a parcurge pașii.
| Set de date | |||||
|---|---|---|---|---|---|
| 46 | 69 | 32 | 60 | 52 | 41 |
Pasul 1: Se face un set de date: Găsiți media
Pentru a găsi media, adunați toate scorurile, apoi împărțiți-le la numărul de scoruri.
x̅ = (46 + 69 + 32 + 60 + 52 + 41) ÷ 6 = 50
Pasul 2: Găsiți abaterea fiecărui punctaj de la medie
Substrăgeți media din fiecare punctaj pentru a obține abaterile de la medie.
Din moment ce x̅ = 50, aici scădem 50 din fiecare scor.
| Score | Ecart de la medie |
|---|---|
| 46 | 46 – 50 = -4 |
| 69 | 69 – 50 = 19 |
| 32 | 32 – 50 = -18 |
| 60 | 60 – 50 = 10 |
| 52 | 52 – 50 = 2 |
| 41 | 41 – 50 = -9 |
Pasul 3: Se ridică la pătrat fiecare abatere de la medie
Se înmulțește fiecare abatere de la medie cu ea însăși. Acest lucru va rezulta în numere pozitive.
(-4)2 = 4 × 4 = 16
192 = 19 × 19 = 361
(-18)2 = -18 × -18 = 324
102 = 10 × 10 = 100
22 = 2 × 2 = 4
(-9)2 = -9 × -9 = 81
Pasul 4: Găsiți suma pătratelor
Adunați toate abaterile la pătrat. Aceasta se numește suma pătratelor.
16 + 361 + 324 + 100 + 4 + 81 = 886
Pasul 5: Găsiți varianța
Divizați suma pătratelor cu n – 1 (pentru un eșantion) sau N (pentru o populație) – aceasta este varianța.
Din moment ce lucrăm cu un eșantion de 6, vom folosi n – 1, unde n = 6.
886 ÷ (6 – 1) = 886 ÷ 5 = 177.2
Pasul 6: Găsiți rădăcina pătrată a varianței
Pentru a găsi abaterea standard, luăm rădăcina pătrată a varianței.
√177.2 = 13.31
Din învățarea că SD = 13.31, putem spune că fiecare scor se abate în medie cu 13,31 puncte de la medie.
De ce este abaterea standard o măsură utilă a variabilității?
Deși există modalități mai simple de a calcula variabilitatea, formula abaterii standard cântărește mai mult eșantioanele repartizate inegal decât eșantioanele repartizate uniform. O abatere standard mai mare vă spune că distribuția nu este doar mai răspândită, ci și mai neuniformă.
Aceasta înseamnă că vă oferă o idee mai bună despre variabilitatea datelor dvs. decât măsuri mai simple, cum ar fi abaterea medie absolută (MAD).
DAM este similară cu abaterea standard, dar mai ușor de calculat. În primul rând, exprimați fiecare abatere de la medie în valori absolute, transformându-le în numere pozitive (de exemplu, -3 devine 3). Apoi, calculați media acestor abateri absolute.
Dincolo de abaterea standard, nu trebuie să calculați pătrate sau rădăcini pătrate ale numerelor pentru MAD. Cu toate acestea, din acest motiv, ea vă oferă o măsură mai puțin precisă a variabilității.
Să luăm două eșantioane cu aceeași tendință centrală, dar cu valori diferite de variabilitate. Eșantionul B este mai variabil decât eșantionul A.
| Valori | Mediu | Deviația absolută medie | Deviația standard | |
|---|---|---|---|---|
| Eșantionul A | 66, 30, 40, 64 | 50 | 15 | 17.8 |
| Eșantionul B | 51, 21, 79, 49 | 50 | 15 | 23.7 |
Pentru eșantioane cu abateri medii egale de la medie, MAD nu poate diferenția nivelurile de dispersie. Abaterea standard este mai precisă: este mai mare pentru eșantionul cu o variabilitate mai mare a abaterilor de la medie.
Prin ridicarea la pătrat a diferențelor față de medie, abaterea standard reflectă cu mai multă acuratețe dispersia inegală. Acest pas cântărește mai mult abaterile extreme decât abaterile mici.
Dar, acest lucru face, de asemenea, ca abaterea standard să fie sensibilă la valorile aberante.
Întrebări frecvente despre abaterea standard
Variabilitatea este cel mai frecvent măsurată cu ajutorul următoarelor statistici descriptive:
- Interval: diferența dintre cea mai mare și cea mai mică valoare
- Interval interquartil: intervalul jumătății medii a unei distribuții
- Abaterea standard: distanța medie față de medie
- Varianța: media distanțelor pătratice față de medie
Deviația standard este valoarea medie a variabilității din setul dumneavoastră de date. Ea vă spune, în medie, cât de departe se află fiecare scor de medie.
În distribuțiile normale, o abatere standard mare înseamnă că valorile sunt, în general, departe de medie, în timp ce o abatere standard mică indică faptul că valorile sunt grupate aproape de medie.
Într-o distribuție normală, datele sunt distribuite simetric, fără distorsiuni. Cele mai multe valori se grupează în jurul unei regiuni centrale, valorile scăzând pe măsură ce se îndepărtează de centru.
Măsurile tendinței centrale (media, modul și mediana) sunt exact aceleași într-o distribuție normală.
Regula empirică, sau regula 68-95-99,7, vă spune unde se află majoritatea valorilor într-o distribuție normală:
- În jur de 68% din valori se află în interiorul unei deviații standard a mediei.
- În jur de 95% din valori se află în interiorul a 2 deviații standard a mediei.
- În jur de 99.7% din valori se încadrează în 3 abateri standard de la medie.
Regula empirică este o modalitate rapidă de a obține o imagine de ansamblu a datelor dvs. și de a verifica dacă există valori aberante sau extreme care nu urmează acest model.
Varianța este media abaterilor la pătrat de la medie, în timp ce abaterea standard este rădăcina pătrată a acestui număr. Ambele măsuri reflectă variabilitatea unei distribuții, dar unitățile lor diferă:
- Deviația standard este exprimată în aceleași unități ca și valorile originale (de exemplu, minute sau metri).
- Varianța este exprimată în unități mult mai mari (de exemplu, metri la pătrat).
Deși unitățile de măsură ale varianței sunt mai greu de înțeles intuitiv, varianța este importantă în testele statistice.
.