Resposta 7 – 7 – 7 = 73 Esta passagem é lida como “sete cubos”

Exponentes e Raízes Quadradas

Objectivo(s)-Learning Objective(s)

– Avaliar expressões contendo expoentes.

– Escrever factores repetidos usando notação exponencial.

– Encontrar uma raiz quadrada de um quadrado perfeito.

Exponentes fornecem uma forma especial de escrever multiplicação repetida. Números escritos desta forma têm uma forma específica, com cada parte fornecendo informações importantes sobre o número. Escrever números usando expoentes também pode economizar muito espaço. A operação inversa de multiplicação de um número por si só é chamada de encontrar a raiz quadrada de um número. Esta operação é útil para problemas sobre a área de um quadrado.

Notação Exponencial é uma forma especial de escrever fatores repetidos, por exemplo 7 – 7. Notação exponencial tem duas partes. Uma parte da notação é chamada de base. A base é o número que está sendo multiplicado por si mesma. A outra parte da notação é o expoente, ou poder. Este é o pequeno número escrito no alto à direita da base. O expoente, ou poder, diz quantas vezes usar a base como um fator na multiplicação. No exemplo, 7 – 7 pode ser escrito como 72, 7 é a base e 2 é o expoente. O expoente 2 significa que existem dois fatores.

72 = 7 – 7 = 49

Você pode ler 72 como “sete ao quadrado”. Isto é porque multiplicar um número por si só é chamado de “quadrado um número”. Da mesma forma, elevar um número até uma potência de 3 chama-se “cubar o número”. Você pode ler 73 como “sete ao cubo”

Você pode ler 25 como “dois para a quinta potência” ou “dois para a potência de cinco”. Leia 84 como “oito para a quarta potência” ou “oito para a potência de quatro”. Este formato pode ser usado para ler qualquer número escrito em notação exponencial. Na verdade, enquanto 63 é mais comum ler “seis ao cubo”, também pode ser lido “seis à terceira potência” ou “seis à potência de três”

Para encontrar o valor de um número escrito de forma exponencial, reescreva o número como multiplicação repetida e faça a multiplicação. Dois exemplos são mostrados abaixo.”

Passar a encontrar o valor de 43.

A) 12

B) 64

C) 256

D) 43

Escrever multiplicação repetida em notação exponencial pode poupar tempo e espaço. Considere o exemplo 5 – 5 – 5 – 5 – 5. Podemos usar notação exponencial para escrever esta multiplicação repetida como 54. Como 5 está sendo multiplicado, ele é escrito como a base. Como a base é usada 4 vezes na multiplicação, o expoente é 4. A expressão 5 – 5 – 5 – 5 pode ser reescrita em notação exponencial curta como 54 e é lida, “cinco para a quarta potência” ou “cinco para a potência de 4”

Para escrever multiplicação repetida do mesmo número em notação exponencial, primeiro escreva o número sendo multiplicado como a base. Depois conte quantas vezes esse número é usado na multiplicação, e escreva esse número como o expoente. Certifique-se de contar os números, não os sinais de multiplicação, para determinar o expoente.

Escreve 10 – 10 – 10 – 10 – 10 – 10 – 10 em notação exponencial.

A) 1.000.000

B) 60

C) 105

D) 106

Como você viu antes, 52 é chamado de “cinco ao quadrado”. “Cinco ao quadrado” significa multiplicar cinco por si mesmo. Em matemática, nós chamamos multiplicar um número por si só de “quadrado” o número. Nós chamamos o resultado da quadratura de um número inteiro de um quadrado ou um quadrado perfeito. Um quadrado perfeito é qualquer número que pode ser escrito como um número inteiro elevado à potência de 2. Por exemplo, 9 é um quadrado perfeito. Um número quadrado perfeito pode ser representado como uma forma quadrada, como mostrado abaixo. Vemos que 1, 4, 9, 16, 16, 25 e 36 são exemplos de quadrados perfeitos.

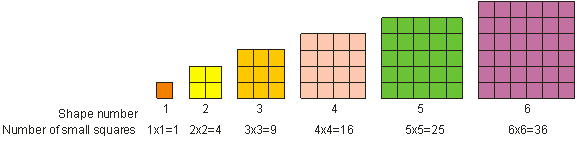
Para ajustar um número ao quadrado, multiplique o número por si mesmo. 3 quadrados = 32 = 3 – 3 = 9.

Below são mais alguns exemplos de quadrados perfeitos.

A operação inversa do quadrado de um número é chamada de encontrar a raiz quadrada de um número. Encontrar uma raiz quadrada é como perguntar: “que número multiplicado por si mesmo me dará este número?” A raiz quadrada de 25 é 5, porque 5 multiplicado por si mesmo é igual a 25. As raízes quadradas são escritas com o símbolo matemático, chamado sinal radical, que se parece com isto: . A “raiz quadrada de 25” é escrita .

Localizar .

A) 6

B) 18

C) 72

D) 7

Notação exponencial é uma forma abreviada de escrever multiplicação repetida do mesmo número. Um número escrito em notação exponencial tem uma base e um expoente, e cada uma destas partes fornece informações para encontrar o valor da expressão. A base diz qual número está sendo multiplicado repetidamente, e o expoente diz quantas vezes a base é usada na multiplicação. Os expoentes 2 e 3 têm nomes especiais. Aumentar uma base para um poder de 2 é chamado de “quadratura” de um número. Aumentar uma base para um poder de 3 é chamado de “cubar” um número. O inverso da quadratura de um número é encontrar a raiz quadrada de um número. Para encontrar a raiz quadrada de um número, pergunte-se: “Que número posso multiplicar por si só para obter este número?”