Odchylenie standardowe jest średnią ilością zmienności w twoim zestawie danych. Mówi ono, średnio, jak daleko każda wartość leży od średniej.
Wysokie odchylenie standardowe oznacza, że wartości są generalnie daleko od średniej, podczas gdy niskie odchylenie standardowe wskazuje, że wartości są skupione blisko średniej.
Co mówi Ci odchylenie standardowe?
Odchylenie standardowe jest użyteczną miarą rozrzutu dla rozkładów normalnych.
W rozkładach normalnych dane są symetrycznie rozłożone bez skosu. Większość wartości skupia się wokół centralnego regionu, a wartości zmniejszają się wraz z oddalaniem się od centrum. Odchylenie standardowe mówi, jak bardzo dane są średnio oddalone od centrum rozkładu.
Wiele zmiennych naukowych ma rozkład normalny, w tym wzrost, wyniki standaryzowanych testów lub oceny zadowolenia z pracy. Kiedy mamy odchylenia standardowe różnych próbek, możemy porównać ich rozkłady za pomocą testów statystycznych, aby wnioskować o większych populacjach, z których pochodzą.
Średnie (M) oceny są takie same dla każdej grupy – jest to wartość na osi x, gdy krzywa jest w punkcie szczytowym. Jednak ich odchylenia standardowe (SD) różnią się od siebie.
Odchylenie standardowe odzwierciedla rozproszenie rozkładu. Krzywa o najniższym odchyleniu standardowym ma wysoki szczyt i małą rozpiętość, podczas gdy krzywa o najwyższym odchyleniu standardowym jest bardziej płaska i rozległa.
Reguła empiryczna
Odchylenie standardowe i średnia razem mogą powiedzieć, gdzie leży większość wartości w twoim rozkładzie, jeśli są one zgodne z rozkładem normalnym.
Reguła empiryczna, lub reguła 68-95-99.7, mówi ci, gdzie leżą twoje wartości:
- Około 68% wyników jest w granicach 2 odchyleń standardowych od średniej,
- Około 95% wyników jest w granicach 4 odchyleń standardowych od średniej,
- Około 99.7% wyników mieści się w granicach 6 odchyleń standardowych od średniej.
Postępując zgodnie z regułą empiryczną:
- Około 68% wyników znajduje się w przedziale od 40 do 60.
- Około 95% wyników znajduje się w przedziale od 30 do 70.
- Około 99,7% wyników znajduje się w przedziale od 20 do 80.
Reguła empiryczna jest szybkim sposobem na uzyskanie przeglądu danych i sprawdzenie, czy nie ma wartości odstających lub skrajnych, które nie podążają za tym wzorcem.
W przypadku rozkładów innych niż normalny, odchylenie standardowe jest mniej wiarygodną miarą zmienności i powinno być używane w połączeniu z innymi miarami, takimi jak zakres lub przedział międzykwartylowy.
Wzory na odchylenie standardowe dla populacji i próbek
Różne wzory są używane do obliczania odchyleń standardowych w zależności od tego, czy mamy dane z całej populacji czy z próbki.
Populacyjne odchylenie standardowe
Gdy masz zebrane dane od każdego członka populacji, którą jesteś zainteresowany, możesz otrzymać dokładną wartość dla populacyjnego odchylenia standardowego.
Sformułowanie na odchylenie standardowe populacji wygląda następująco:
| Formuła | Wyjaśnienie |
|---|---|
 |
|
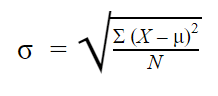Odchylenie standardowe z próby
Gdy zbierasz dane z próby, odchylenie standardowe z próby jest używane do szacowania lub wnioskowania o odchyleniu standardowym populacji.
Sformułowanie na odchylenie standardowe próby wygląda następująco:
| Formuła | Wyjaśnienie |
|---|---|
 |
|
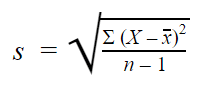W przypadku prób używamy n – 1 we wzorze, ponieważ użycie n dałoby nam tendencyjne oszacowanie, które konsekwentnie niedoszacowuje zmienność. Odchylenie standardowe próbki byłoby zwykle niższe niż rzeczywiste odchylenie standardowe populacji.
Zmniejszenie próbki n do n – 1 powoduje, że odchylenie standardowe jest sztucznie duże, co daje konserwatywne oszacowanie zmienności.
Chociaż nie jest to nieobiektywne oszacowanie, jest to mniej nieobiektywne oszacowanie odchylenia standardowego: lepiej jest przeszacować niż niedoszacować zmienność w próbkach.
Kroki obliczania odchylenia standardowego
Odchylenie standardowe jest zwykle obliczane automatycznie przez dowolne oprogramowanie używane do analizy statystycznej. Ale możesz również obliczyć je ręcznie, aby lepiej zrozumieć jak działa ta formuła.
Istnieje sześć głównych kroków do ręcznego znalezienia odchylenia standardowego. Użyjemy małego zestawu danych z 6 wynikami, aby przejść przez te kroki.
| Zestaw danych | |||||
|---|---|---|---|---|---|
| 46 | 69 | 32 | 60 | 52 | 41 |
Krok 1: Znajdź średnią
Aby znaleźć średnią, zsumuj wszystkie wyniki, a następnie podziel je przez liczbę wyników.
x̅ = (46 + 69 + 32 + 60 + 52 + 41) ÷ 6 = 50
Krok 2: Znajdź odchylenie każdego wyniku od średniej
Od każdego wyniku odejmij średnią, aby otrzymać odchylenia od średniej.
Ponieważ x̅ = 50, tutaj odejmiemy 50 od każdego wyniku.
| Score | Odchylenie od średniej |
|---|---|
| 46 | 46 – 50 = -.4 |
| 69 | 69 – 50 = 19 |
| 32 | 32 – 50 = -18 |
| 60 | 60 – 50 = 10 |
| 52 | 52 – 50 = 2 |
| 41 | 41 – 50 = -9 |
Krok 3: Podnieść do kwadratu każde odchylenie od średniej
Mnożymy każde odchylenie od średniej przez siebie. W ten sposób otrzymamy liczby dodatnie.
(-4)2 = 4 × 4 = 16
192 = 19 × 19 = 361
(-18)2 = -.18 × -18 = 324
102 = 10 × 10 = 100
22 = 2 × 2 = 4
(-9)2 = -9 × -9 = 81
Krok 4: Znajdź sumę kwadratów
Dodaj wszystkie odchylenia kwadratowe. To się nazywa suma kwadratów.
16 + 361 + 324 + 100 + 4 + 81 = 886
Krok 5: Znajdź wariancję
Podziel sumę kwadratów przez n – 1 (dla próbki) lub N (dla populacji) – to jest wariancja.
Ponieważ pracujemy z próbką o liczebności 6, użyjemy n – 1, gdzie n = 6.
886 ÷ (6 – 1) = 886 ÷ 5 = 177.2
Krok 6: Znajdź pierwiastek kwadratowy z wariancji
Aby znaleźć odchylenie standardowe, bierzemy pierwiastek kwadratowy z wariancji.
√177,2 = 13,31
Z dowiadując się, że SD = 13.31, możemy powiedzieć, że każdy wynik odchyla się od średniej średnio o 13,31 punktu.
Dlaczego odchylenie standardowe jest użyteczną miarą zmienności?
Pomimo że istnieją prostsze sposoby obliczania zmienności, wzór na odchylenie standardowe waży nierównomiernie rozłożone próbki bardziej niż równomiernie rozłożone próbki. Wyższe odchylenie standardowe mówi, że rozkład jest nie tylko bardziej rozłożony, ale także bardziej nierównomiernie rozłożony.
To oznacza, że daje lepsze pojęcie o zmienności danych niż prostsze miary, takie jak średnie odchylenie bezwzględne (MAD).
MAD jest podobne do odchylenia standardowego, ale łatwiejsze do obliczenia. Po pierwsze, wyrażamy każde odchylenie od średniej w wartościach bezwzględnych, zamieniając je na liczby dodatnie (na przykład, -3 staje się 3). Następnie obliczamy średnią tych bezwzględnych odchyleń.
W przeciwieństwie do odchylenia standardowego, nie musimy obliczać kwadratów lub pierwiastków kwadratowych liczb dla MAD. Jednak z tego powodu daje ona mniej precyzyjną miarę zmienności.
Weźmy dwie próbki o tej samej tendencji centralnej, ale o różnej zmienności. Próbka B jest bardziej zmienna niż próbka A.
| Wartości | Średnia | Średnie odchylenie bezwzględne | Odchylenie standardowe | |
|---|---|---|---|---|
| Próbka A | 66, 30, 40, 64 | 50 | 15 | 17.8 |
| Próba B | 51, 21, 79, 49 | 50 | 15 | 23.7 |
Dla prób o równych średnich odchyleniach od średniej, MAD nie może rozróżnić poziomów rozrzutu. Odchylenie standardowe jest bardziej precyzyjne: jest wyższe dla próbki z większą zmiennością odchyleń od średniej.
Poprzez podniesienie do kwadratu różnic od średniej, odchylenie standardowe dokładniej odzwierciedla nierównomierne rozproszenie. Ten krok waży skrajne odchylenia bardziej niż małe odchylenia.
Jednakże to również czyni odchylenie standardowe wrażliwym na wartości odstające.
Często zadawane pytania dotyczące odchylenia standardowego
Zmienność jest najczęściej mierzona za pomocą następujących statystyk opisowych:
- Rozstęp: różnica między najwyższą i najniższą wartością
- Rozstęp międzykwartylowy: zakres środkowej połowy rozkładu
- Odchylenie standardowe: średnia odległość od średniej
- Wariancja: średnia kwadratów odległości od średniej
Odchylenie standardowe jest średnią ilością zmienności w twoim zestawie danych. Mówi ci, średnio, jak daleko każdy wynik leży od średniej.
W rozkładzie normalnym, wysokie odchylenie standardowe oznacza, że wartości są generalnie daleko od średniej, podczas gdy niskie odchylenie standardowe wskazuje, że wartości są skupione blisko średniej.
W rozkładzie normalnym, dane są symetrycznie rozłożone bez przechylenia. Większość wartości skupia się wokół centralnego regionu, a wartości zmniejszają się wraz z oddalaniem się od centrum.
Miary tendencji centralnej (średnia, tryb i mediana) są dokładnie takie same w rozkładzie normalnym.
Reguła empiryczna, lub reguła 68-95-99,7, mówi, gdzie leży większość wartości w rozkładzie normalnym:
- Około 68% wartości znajduje się w granicach 1 odchylenia standardowego od średniej.
- Około 95% wartości znajduje się w granicach 2 odchyleń standardowych od średniej.
- Około 99.7% wartości mieści się w granicach 3 odchyleń standardowych od średniej.
Reguła empiryczna to szybki sposób na uzyskanie przeglądu danych i sprawdzenie, czy nie ma wartości odstających lub skrajnych, które nie podążają za tym wzorcem.
Wariancja jest średnim kwadratem odchylenia od średniej, podczas gdy odchylenie standardowe jest pierwiastkiem kwadratowym z tej liczby. Obie miary odzwierciedlają zmienność rozkładu, ale ich jednostki różnią się:
- Odchylenie standardowe jest wyrażane w tych samych jednostkach, co wartości początkowe (np. minuty lub metry).
- Wariancja jest wyrażana w znacznie większych jednostkach (np. metry podniesione do kwadratu).
Mimo że jednostki wariancji są trudniejsze do intuicyjnego zrozumienia, wariancja jest ważna w testach statystycznych.
.