W tej lekcji pokażemy łatwą strategię rozwiązywania następującego problemu: jak znaleźć pole trójkąta równoramiennego.
Wprowadźmy w życie kilka własności, które udowodniliśmy do tej pory, w następującym problemie geometrycznym:
Problem
W trójkącie równoramiennym ΔABC o nodze długości 10, wysokość poprowadzona do podstawy jest równa dwóm trzecim podstawy. Znajdź pole tego trójkąta.
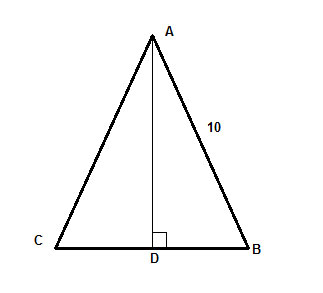
Strategia
Aby rozwiązać ten problem, będziemy pracować wstecz od tego, co musimy zrobić.
Musimy znaleźć pole trójkąta, które, jak wiemy, jest dane wzorem (podstawa razy wysokość)/2.
Problemem, który mamy, jest to, że nie znamy ani długości podstawy, ani wysokości. Ale mamy podaną zależność między nimi, która jest podpowiedzią, co musimy zrobić. Nazwijmy długość podstawy, BC, x.
Wtedy wiemy, że wysokość, AD, jest 2x/3, jak podano w problemie.
Więc odpowiedź, której szukamy to (podstawa razy wysokość)/2, lub x razy 2x/3, podzielone przez dwa.
Ale jak znaleźć x? Są dwie dodatkowe rzeczy, które dostaliśmy w zadaniu, a których jeszcze nie użyliśmy – długość nogi (10) i fakt, że jest to trójkąt równoramienny. Prawdopodobnie będziemy musieli użyć tych dwóch rzeczy do rozwiązania zadania.
Przejrzyjmy własności trójkątów równoramiennych. Jedną z rzeczy, która powinna od razu nasuwać się na myśl jest to, że jak już pokazaliśmy, w trójkącie równoramiennym wysokość poprowadzona do podstawy przecina podstawę, więc CD=DB=x/2.
Wreszcie, AD jest wysokością, co oznacza, że kąt ∠ADC jest kątem prostym i mamy trójkąt prosty, ΔADC, którego hipotensję znamy (10) i możemy użyć do znalezienia nóg używając twierdzenia pitagorejskiego, c2 =a2+b2,
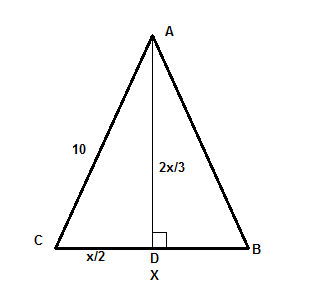
gdzie c= 10 ,a = x/2 i b=2x/3 . I gotowe, reszta to już tylko algebraiczne rozwiązywanie dla x.
Dowód: Pole trójkąta równoramiennego
(1) ΔADC jest trójkątem prostokątnym //dane, ponieważ AD jest wysokością poprowadzoną do podstawy
(2) AC2 =CD2 + AD2 //Twierdzenie Pitagorasa
(3) AC= 10 //dane
(4) CB = x
(5) CD = x/2 //Wysokość poprowadzona do podstawy w trójkącie równoramiennym przecina podstawę
(6) AD = 2x/3 //dane
(7) 102 = (x/2)2 + (2x/3)2 //Substitute into (2)
(8) 100 = x2/4+4×2/9 //simplify
(9) 100*36 = 9×2 +16×2 //multiply both sides by 36
(10) 100*36 = 25×2 //collect similar terms
(10) 100*36 = 25×2