Rozpad neutronu
|
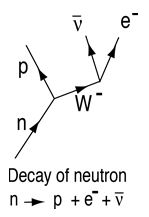
Swobodny neutron rozpada się z czasem połowicznego zaniku około 10,3 minuty, ale jest stabilny, jeśli połączy się z jądrem. Rozpad ten jest przykładem rozpadu beta z emisją elektronu i antyneutrina elektronowego. Rozpad neutronu wiąże się z oddziaływaniem słabym, jak pokazano na diagramie Feynmana po prawej stronie. |
 |
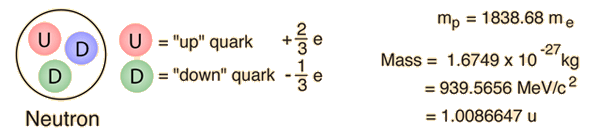
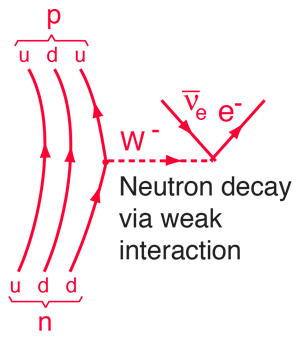 |
Bardziej szczegółowy diagram rozpadu neutronu identyfikuje go jako przemianę jednego z kwarków dołu neutronu w kwark do góry. Jest to przykład tego rodzaju przemian kwarkowych, które są zaangażowane w wiele procesów jądrowych, w tym rozpad beta. |
Rozpad neutronu jest dobrym przykładem obserwacji, które doprowadziły do odkrycia neutrina. Analiza energetyki tego rozpadu może posłużyć do zilustrowania dylematów, przed jakimi stanęli wcześni badacze tego procesu.
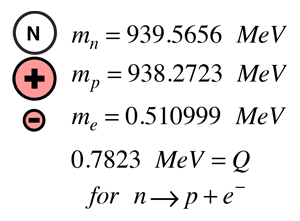 |
Korzystając z pojęcia energii wiązania i reprezentując masy cząstek przez ich energie mas spoczynkowych, można obliczyć wydajność energetyczną z rozpadu neutronu na podstawie mas cząstek. Wydajność energetyczna jest tradycyjnie przedstawiana za pomocą symbolu Q. Ponieważ energia i pęd muszą być zachowane w rozpadzie, zostanie pokazane, że lżejszy elektron będzie zabierał większość energii kinetycznej. Przy tak dużej energii kinetycznej, należy użyć relatywistycznego wyrażenia na energię kinetyczną. |
Na razie zakładamy (błędnie), że rozpad dotyczy tylko protonu i elektronu jako produktów. Wydajność energetyczna Q byłaby wtedy podzielona pomiędzy proton i elektron. Elektron otrzyma większość energii kinetycznej i będzie relatywistyczny, ale proton jest nierelatywistyczny. Bilans energetyczny wynosi wtedy
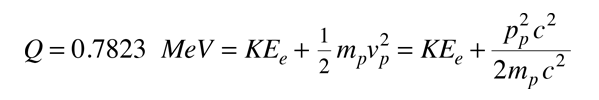
W ramie spoczynkowej neutronu, zachowanie momentu pędu wymaga
W ramie spoczynkowej neutronu pcproton
i pcelektron może być wyrażony w kategoriach energii kinetycznej elektronu
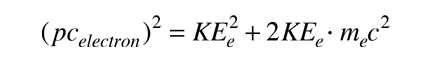 |
Show |
Bilans energetyczny staje się wtedy
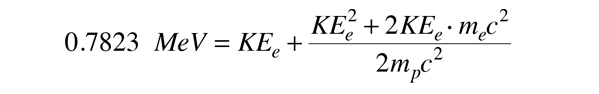
Gdy podstawisz liczby dla tej wartości Q, widzimy, że składnik KEe2 jest pomijalny, więc wymagana energia kinetyczna elektronu może być obliczona. Wymagana energia kinetyczna elektronu dla tego schematu rozpadu dwucząsteczkowego wynosi
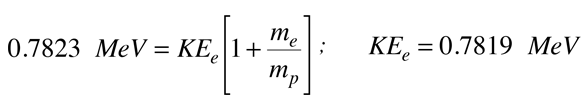
Podobnie, pęd elektronu dla tego rozpadu dwucząsteczkowego jest ograniczony do wartości

Pęd i energia dla rozpadu dwucząsteczkowego są ograniczone do tych wartości, ale tak nie zachowuje się przyroda. Obserwowane rozkłady pędu i energii dla elektronu są takie, jak pokazano poniżej.
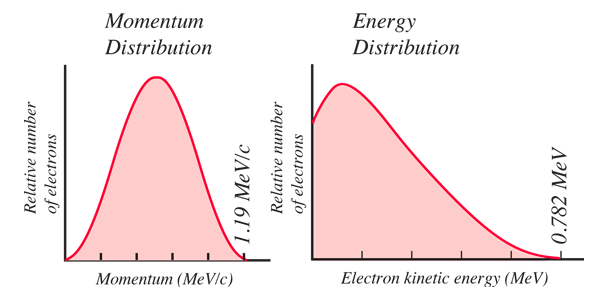
Fakt, że elektrony powstałe z rozpadu neutronu miały ciągłe rozkłady energii i pędu był wyraźną wskazówką, że wraz z elektronem i protonem wyemitowana została inna cząstka. Musiała to być cząstka neutralna i w pewnych rozpadach przenosiła prawie całą energię i pęd rozpadu. Nie byłoby w tym nic nadzwyczajnego, gdyby nie fakt, że kiedy elektron miał swoją maksymalną energię kinetyczną, odpowiadał za całą energię Q dostępną dla rozpadu. Nie pozostała więc żadna energia, która mogłaby być wykorzystana na energię masową innej emitowanej cząstki. Wcześni eksperymentatorzy stanęli przed dylematem cząstki, która mogła przenieść prawie całą energię i pęd rozpadu, ale która nie miała ładunku i najwyraźniej nie miała masy!
Tajemnicza cząstka została nazwana neutrinem, ale minęło dwadzieścia pięć lat, zanim jednoznaczna eksperymentalna obserwacja neutrina została dokonana przez Cowana i Reinesa. Obecne rozumienie rozpadu neutronu jest
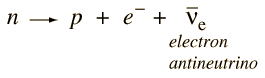
Rozpad ten ilustruje niektóre z praw zachowania, które rządzą rozpadami cząstek. Proton w produkcie spełnia zasadę zachowania liczby barionowej, ale pojawienie się elektronu bez towarzyszenia naruszyłoby zasadę zachowania liczby leptonowej. Trzecią cząstką musi być antyneutrino elektronowe, aby rozpad spełniał warunek zachowania liczby leptonowej. Elektron ma liczbę leptonową 1, a antyneutrino ma liczbę leptonową -1.
Doświadczalne wykrywanie neutrin
Stabilność neutronu w deuteronie