Odpowiedź 7 – 7 – 7 = 73 To jest czytane jako „siedem sześcianów.”

Understanding Exponents and Square Roots

Learning Objective(s)

– Oceniaj wyrażenia zawierające wykładniki.

– Zapisać powtarzające się czynniki używając notacji wykładniczej.

– Znaleźć pierwiastek kwadratowy z kwadratu doskonałego.

Eksponenty zapewniają specjalny sposób zapisu powtarzającego się mnożenia. Liczby zapisane w ten sposób mają specyficzną postać, z każdą częścią dostarczającą ważnych informacji o liczbie. Zapisywanie liczb za pomocą wykładników pozwala również zaoszczędzić sporo miejsca. Operacja odwrotna do mnożenia liczby przez siebie jest nazywana znajdowaniem pierwiastka kwadratowego z liczby. Ta operacja jest pomocna w problemach dotyczących powierzchni kwadratu.

Notacja wykładnicza jest specjalnym sposobem zapisu powtarzających się czynników, na przykład 7 – 7. Notacja wykładnicza ma dwie części. Jedna część notacji jest nazywana podstawą. Podstawą jest liczba, która jest mnożona przez siebie. Druga część notacji to wykładnik, czyli potęga. Jest to mała liczba zapisana wysoko na prawo od podstawy. Wykładnik, lub potęga, mówi ile razy użyć podstawy jako czynnika w mnożeniu. W przykładzie, 7 – 7 może być zapisane jako 72, 7 jest podstawą, a 2 jest wykładnikiem. Wykładnik 2 oznacza, że są dwa czynniki.

72 = 7 – 7 = 49

Możesz przeczytać 72 jako „siedem podniesione do kwadratu”. To dlatego, że mnożenie liczby przez siebie jest nazywane „kwadraturą liczby”. Podobnie, podnoszenie liczby do potęgi 3 jest nazywane „sześcienną liczbą”. Możesz przeczytać 73 jako „siedem podniesione do sześcianu.”

Możesz przeczytać 25 jako „dwie do piątej potęgi” lub „dwie do potęgi piątej.” Możesz odczytać 84 jako „osiem do czwartej potęgi” lub „osiem do potęgi czwartej”. Ten format może być używany do czytania dowolnej liczby zapisanej w notacji wykładniczej. W rzeczywistości, podczas gdy 63 jest najczęściej odczytywane jako „sześć sześcienne”, może być również odczytywane jako „sześć do trzeciej potęgi” lub „sześć do potęgi trzeciej.”

Aby znaleźć wartość liczby zapisanej w postaci wykładniczej, przepisz liczbę jako powtarzające się mnożenie i wykonaj mnożenie. Poniżej przedstawiono dwa przykłady.

Znajdź wartość liczby 43.

A) 12

B) 64

C) 256

D) 43

Pisanie mnożenia wielokrotnego w notacji wykładniczej pozwala zaoszczędzić czas i miejsce. Rozważmy przykład 5 – 5 – 5 – 5. Możemy użyć notacji wykładniczej, aby zapisać to powtarzające się mnożenie jako 54. Ponieważ 5 jest mnożone, jest ono zapisane jako podstawa. Ponieważ podstawa jest używana 4 razy w mnożeniu, wykładnikiem jest 4. Wyrażenie 5 – 5 – 5 – 5 może być przepisane w skróconej notacji wykładniczej jako 54 i jest odczytywane jako „pięć do czwartej potęgi” lub „pięć do potęgi 4.”

Aby napisać wielokrotne mnożenie tej samej liczby w notacji wykładniczej, najpierw napisz liczbę mnożoną jako podstawę. Następnie policz, ile razy ta liczba jest używana w mnożeniu, i zapisz tę liczbę jako wykładnik. Pamiętaj o liczeniu liczb, a nie znaków mnożenia, aby określić wykładnik.

Zapisz 10 – 10 – 10 – 10 – 10 – 10 – 10 w notacji wykładniczej.

A) 1.000.000

B) 60

C) 105

D) 106

Jak już wcześniej zauważyłeś, 52 jest nazywane „piątką podniesioną do kwadratu”. „Pięć podniesione do kwadratu” oznacza pomnożenie pięciu przez siebie. W matematyce mnożenie liczby przez siebie nazywamy „kwadratowaniem” tej liczby. Wynik kwadratury liczby całkowitej nazywamy kwadratem lub kwadratem doskonałym. Kwadratem doskonałym jest każda liczba, która może być zapisana jako liczba całkowita podniesiona do potęgi 2. Na przykład 9 jest kwadratem doskonałym. Liczba doskonała kwadratowa może być przedstawiona jako kształt kwadratu, jak pokazano poniżej. Widzimy, że 1, 4, 9, 16, 25 i 36 są przykładami kwadratów doskonałych.

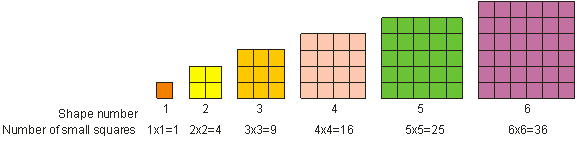
Aby podnieść liczbę do kwadratu, należy ją pomnożyć przez siebie. 3 podniesione do kwadratu = 32 = 3 – 3 = 9.

Poniżej jest jeszcze kilka przykładów kwadratów doskonałych.

22

2 – 2

4

3 podniesione do kwadratu

32

3 – 3

9

4 podniesione do kwadratu

42

4 – 4

16

.

62

6 – 6

36

7 podniesiony do kwadratu

72

7 – 7

.

49

8 podniesione do kwadratu

82

8 – 8

64

.

9 do kwadratu

92

9 – 9

81

10 do kwadratu

102

10 – 10

100

Odwrotna operacja kwadratowania liczby nazywana jest znajdowaniem pierwiastka kwadratowego z liczby. Znajdowanie pierwiastka kwadratowego jest jak pytanie: „jaka liczba pomnożona przez siebie da mi tę liczbę?”. Pierwiastek kwadratowy z 25 to 5, ponieważ 5 pomnożone przez siebie jest równe 25. Pierwiastki kwadratowe zapisuje się za pomocą symbolu matematycznego, zwanego znakiem rodnika, który wygląda tak: . Pierwiastek kwadratowy z 25″ zapisuje się .

Znajdź .

A) 6

B) 18

C) 72

D) 7

Notacja wykładnicza to skrótowy sposób zapisu wielokrotnego mnożenia tej samej liczby. Liczba zapisana w notacji wykładniczej ma podstawę i wykładnik, a każda z tych części dostarcza informacji do znalezienia wartości wyrażenia. Podstawa mówi, jaka liczba jest wielokrotnie mnożona, a wykładnik mówi, ile razy podstawa jest używana w mnożeniu. Wykładniki 2 i 3 mają specjalne nazwy. Podniesienie podstawy do potęgi 2 jest nazywane „kwadratowaniem” liczby. Podnoszenie podstawy do potęgi 3 jest nazywane „sześciennym” mnożeniem liczby. Odwrotnością kwadratury liczby jest znalezienie pierwiastka kwadratowego z liczby. Aby znaleźć pierwiastek kwadratowy z liczby, zadaj sobie pytanie: „Jaką liczbę mogę pomnożyć przez siebie, aby otrzymać tę liczbę?”

.