
The Policy Question: Hybrid Car Purchase Tax Credit-Is it the Government’s Best Choice to Reduce Fuel Consumption and Carbon Emissions?
Mieszkańcy USA i rząd są zaniepokojeni zależnością od importowanej zagranicznej ropy naftowej i uwalnianiem węgla do atmosfery. W 2005 r. Kongres uchwalił ustawę zapewniającą konsumentom ulgi podatkowe na zakup samochodów elektrycznych i hybrydowych.
Ta ulga podatkowa może wydawać się dobrym wyborem politycznym, ale jest kosztowna, ponieważ bezpośrednio obniża kwotę przychodów, które zbiera rząd USA. Czy istnieją bardziej efektywne podejścia do zmniejszenia zależności od paliw kopalnych i emisji dwutlenku węgla? Jak zdecydować, która polityka jest najlepsza? Aby odpowiedzieć na to pytanie, decydenci polityczni muszą przewidzieć z pewną dokładnością, jak konsumenci zareagują na tę politykę podatkową, zanim ci decydenci wydadzą miliony dolarów federalnych.
Możemy zastosować pojęcie użyteczności do tego pytania politycznego. W tym module będziemy badać użyteczność i funkcje użyteczności. Następnie będziemy w stanie użyć odpowiedniej funkcji użyteczności do wyprowadzenia krzywych obojętności, które opisują nasze pytanie dotyczące polityki.
Badanie pytania dotyczącego polityki
Załóżmy, że ulga podatkowa na subsydiowanie zakupu samochodów hybrydowych jest szalenie skuteczna i podwaja średnią oszczędność paliwa wszystkich samochodów na amerykańskich drogach – wynik, który jest wyraźnie nierealistyczny, ale przydatny dla naszych dalszych dyskusji. Jak myślicie, co stałoby się ze zużyciem paliwa przez wszystkich amerykańskich kierowców? Czy rząd powinien oczekiwać, że w odpowiedzi zużycie paliwa i emisja dwutlenku węgla przez samochody spadną o połowę? Dlaczego lub dlaczego nie?
2.1 Funkcje użyteczności
LO 2.1: Opisać funkcję użyteczności.
2.2 Funkcje użyteczności i typowe preferencje
LO 2.2: Identyfikowanie funkcji użyteczności na podstawie typowych preferencji, które reprezentują.
2.3 Odnoszenie funkcji użyteczności i map krzywych obojętności
LO 2.3: Wyjaśnić, jak wyprowadzić krzywą obojętności z funkcji użyteczności.
2.4 Znajdowanie użyteczności krańcowej i krańcowej stopy substytucji
LO 2.4: Wyznaczyć użyteczność krańcową i MRS dla typowych funkcji użyteczności.
2.5. Pytanie dotyczące polityki
2.1 Funkcje użyteczności
LO1: Opisać funkcję użyteczności.
Nasze preferencje pozwalają nam dokonywać porównań pomiędzy różnymi pakietami konsumpcyjnymi i wybierać preferowane pakiety. Możemy, na przykład, określić kolejność całego zestawu pakietów w oparciu o nasze preferencje. Funkcja użyteczności jest funkcją matematyczną, która szereguje wiązki dóbr konsumpcyjnych poprzez przypisanie każdej z nich liczby, gdzie większe liczby oznaczają wiązki preferowane. Funkcje użyteczności mają właściwości, które zidentyfikowaliśmy w Module 1 w odniesieniu do preferencji. To znaczy: są w stanie uporządkować wiązki, są kompletne i przechodnie, więcej jest preferowane niż mniej, a w odpowiednich przypadkach mieszane wiązki są lepsze.
Liczba, którą funkcja użyteczności przypisuje konkretnej wiązce jest znana jako użyteczność, satysfakcja, jaką konsument uzyskuje z konkretnej wiązki. Liczba użyteczności dla każdego pakietu nie oznacza nic w kategoriach absolutnych; nie ma jednolitej skali, według której mierzymy satysfakcję. Jedyne jej zastosowanie jest względne: możemy użyć użyteczności do określenia, które pakiety są preferowane względem innych.
Jeśli użyteczność z pakietu A jest wyższa niż użyteczność z pakietu B, jest to równoważne stwierdzeniu, że konsument woli pakiet A od pakietu B. Funkcje użyteczności szeregują zatem preferencje konsumentów, przypisując każdemu pakietowi odpowiednią liczbę. . Możemy użyć funkcji użyteczności do narysowania map krzywych obojętności opisanych w module 1. Ponieważ wszystkie pakiety na tej samej krzywej obojętności dają taką samą satysfakcję, a więc żaden z nich nie jest preferowany, każdy pakiet ma taką samą użyteczność. Możemy zatem narysować krzywą obojętności, wyznaczając wszystkie wiązki, które zwracają tę samą liczbę z funkcji użyteczności.
Ekonomiści mówią, że funkcje użyteczności są porządkowe, a nie kardynalne. Porządkowe oznaczają, że funkcje użyteczności jedynie szeregują wiązki – wskazują tylko, która z nich jest lepsza, a nie o ile jest lepsza od innej wiązki. Załóżmy na przykład, że jedna funkcja użyteczności wskazuje, że pakiet A daje 10 utils, a pakiet B 20 utils. Nie mówimy, że pakiet B jest dwa razy lepszy lub o 10 utils lepszy, tylko że konsument woli pakiet B. Załóżmy na przykład, że znajoma wzięła udział w wyścigu i powiedziała Ci, że zajęła trzecie miejsce. Ta informacja jest porządkowa: Wiesz, że była szybsza niż osoba, która zajęła czwarte miejsce i wolniejsza niż osoba, która zajęła drugie miejsce. Znasz tylko kolejność, w jakiej biegacze ukończyli bieg. Poszczególne czasy są kardynalne: Jeśli osoba, która zajęła pierwsze miejsce, przebiegła wyścig dokładnie w godzinę, a Twój przyjaciel w godzinę i sześć minut, to wiesz, że Twój przyjaciel był dokładnie o 10% wolniejszy od najszybszego biegacza. ponieważ funkcje użyteczności są porządkowe, wiele różnych funkcji użyteczności może reprezentować te same preferencje. Jest to prawda tak długo, jak długo zachowane jest uporządkowanie.
Weźmy na przykład funkcję użyteczności U, która opisuje preferencje dotyczące pakietów dóbr A i B: U(A,B). Możemy zastosować do tej funkcji dowolne przekształcenie monotoniczne dodatnie (co oznacza w zasadzie, że nie zmieniamy uporządkowania), a utworzona przez nas nowa funkcja będzie reprezentować te same preferencje. Na przykład, moglibyśmy pomnożyć dodatnią stałą, α , lub dodać dodatnią lub ujemną stałą, β . Zatem αU(A,B)+β reprezentuje dokładnie te same preferencje co U(A,B), ponieważ uporządkuje wiązki w dokładnie taki sam sposób. Ten fakt jest dość użyteczny, ponieważ czasami zastosowanie dodatniej monotonicznej transformacji funkcji użyteczności ułatwia rozwiązywanie problemów.
2.2 Funkcje użyteczności i typowe preferencje
LO2: Określanie funkcji użyteczności na podstawie typowych preferencji, które reprezentują
Rozważmy wiązki jabłek A i bananów B. Funkcją użyteczności, która opisuje preferencje Izaaka dotyczące wiązek jabłek i bananów, jest funkcja U(A,B). Ale jakie są szczególne preferencje Isaaca dotyczące kiści jabłek i bananów? Załóżmy, że Izaak ma dość standardowe preferencje dotyczące jabłek i bananów, które prowadzą do naszych typowych krzywych obojętności: Woli więcej niż mniej i lubi różnorodność. Funkcją użyteczności reprezentującą te preferencje może być:
U(A,B) = AB
Jeśli jabłka i banany są doskonałymi uzupełnieniami w preferencjach Isaaca, funkcja użyteczności wyglądałaby tak:
U(A,B) = MIN,
gdzie funkcja MIN po prostu przypisuje mniejszą z dwóch liczb jako wartość funkcji.
Jeśli jabłka i banany są doskonałymi substytutami, funkcja użyteczności jest addytywna i wyglądałaby mniej więcej tak:
U(A,B) = A + B
Klasa funkcji użyteczności znana jako funkcje użyteczności Cobba-Douglasa jest bardzo powszechnie używana w ekonomii z dwóch powodów:
1. Reprezentują one „dobrze zachowujące się” preferencje, takie jak więcej znaczy lepiej i preferencje różnorodności.
2. Są one bardzo elastyczne i można je bardzo łatwo dopasować do danych ze świata rzeczywistego.
Funkcje użyteczności Cobba-Douglasa mają następującą postać:
U(A,B) = AαBβ
Ponieważ dodatnie monotoniczne transformacje reprezentują te same preferencje, jedna z takich transformacji może być użyta do ustawienia α + β = 1 , co później zobaczymy jako wygodny warunek, który upraszcza niektóre matematyczne zadania w problemie wyboru konsumenta.
Innym sposobem na przekształcenie funkcji użyteczności w użyteczny sposób jest przyjęcie logu naturalnego funkcji, co tworzy nową funkcję, która wygląda tak:
U(A,B) = αln(A) + βln(B)
Aby wyprowadzić to równanie, po prostu zastosuj reguły logów naturalnych. . Ważne jest, aby pamiętać o poziomie abstrakcji. Zazwyczaj nie potrafimy stworzyć konkretnych funkcji użyteczności, które dokładnie opisywałyby indywidualne preferencje. Prawdopodobnie nikt z nas nie mógłby opisać swoich własnych preferencji za pomocą jednego równania. Ale tak długo, jak konsumenci ogólnie mają preferencje zgodne z naszymi podstawowymi założeniami, możemy wykonać całkiem dobrą robotę znajdując funkcje użyteczności, które pasują do danych dotyczących konsumpcji w świecie rzeczywistym. Zobaczymy dowody na to w dalszej części kursu.
Tabela 2.1 podsumowuje preferencje i funkcje użyteczności opisane w tym rozdziale.
|
Tabela 2.1 Rodzaje preferencji i reprezentujące je funkcje użyteczności |
||
|
PREFERENCJE |
FUNKCJA UŻYTECZNOŚCI FUNKCJA |
TYP FUNKCJI UTYLITYCZNEJ |
|
Umiłowanie różnorodności lub „dobrze wychowany” |
U(A,B) = AB |
Cobb-Douglas |
|
Miłość Rozmaitości lub „Dobrze Zachowani” |
U(A,B) = AαBβ |
Cobb-Douglas |
|
Miłość Rozmaitości lub „Dobrze Zachowani” |
U(A,B) = αln(A) + βln(B) |
Naturalny log Cobba-Douglasa |
|
Doskonałe uzupełnienia |
U(A,B) = MIN |
Funkcja Min |
|
Doskonałe Substytuty |
U(A,B) = A + B |
Dodatkowe |
2.3 Relating Utility Functions and Indifference Curve Maps
LO3: Wyjaśnij, jak wyprowadzić krzywą obojętności z funkcji użyteczności
Krzywe obojętności i funkcje użyteczności są ze sobą bezpośrednio powiązane. W rzeczywistości, ponieważ krzywe obojętności przedstawiają preferencje w sposób graficzny, a funkcje użyteczności przedstawiają preferencje w sposób matematyczny, wynika z tego, że krzywe obojętności można wyprowadzić z funkcji użyteczności.
W funkcjach jednowariantowych zmienna zależna jest wykreślana na osi pionowej, a zmienna niezależna na osi poziomej, tak jak wykres y=f(x). W przeciwieństwie do tego wykresy funkcji dwuczynnikowych są trójwymiarowe, jak U=U(A,B). Rysunek 2.1 przedstawia wykres funkcji U=A^^frac{1}{2}B^^frac{1}{2}. Wykresy trójwymiarowe są przydatne do zrozumienia, w jaki sposób użyteczność rośnie wraz ze wzrostem konsumpcji zarówno A, jak i B.
Rysunek 2.1 U=A^frac{1}{2}B^frac{1}{2}
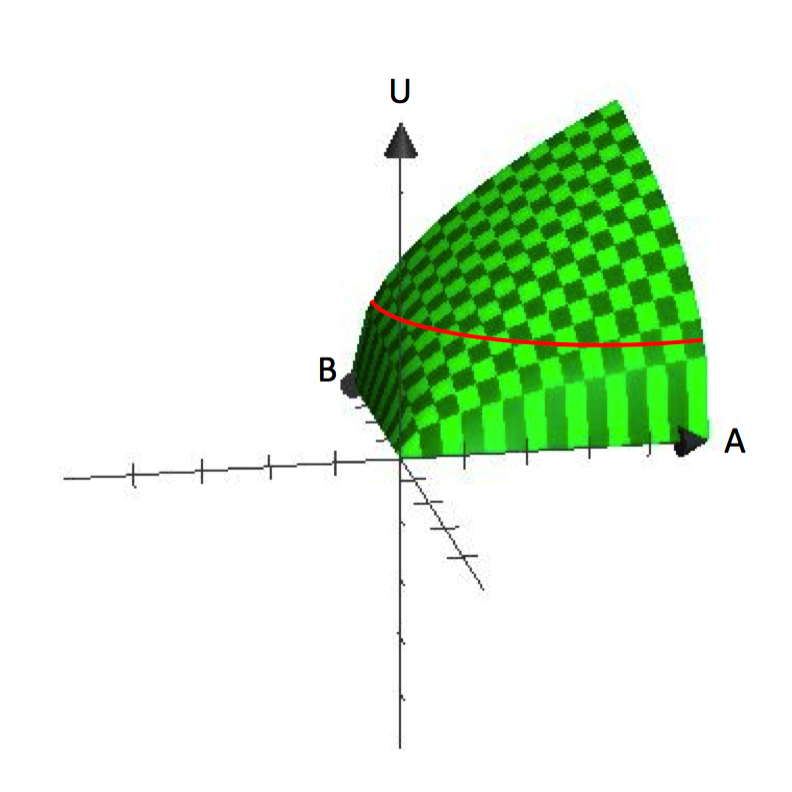
Rysunek 2.1 wyraźnie pokazuje założenie, że konsumenci mają preferencję do różnorodności. Każda wiązka, która zawiera określoną ilość A i B reprezentuje punkt na powierzchni. Pionowa wysokość powierzchni reprezentuje poziom użyteczności. Zwiększając zarówno A, jak i B, konsument może osiągnąć wyższe punkty na powierzchni.
Skąd więc biorą się krzywe obojętności? Przypomnijmy, że krzywa obojętności to zbiór wszystkich pakietów, które są obojętne dla konsumenta, w odniesieniu do tego, który z nich skonsumować. Z matematycznego punktu widzenia jest to równoznaczne z tym, że wszystkie pakiety, włożone do funkcji użyteczności, zwracają tę samą wartość funkcyjną. Jeśli więc ustalimy wartość użyteczności, Ū, i znajdziemy wszystkie wiązki A i B, które generują tę wartość, to wyznaczymy krzywą obojętności. Zauważmy, że jest to równoważne znalezieniu wszystkich wiązek, dzięki którym konsument osiągnie tę samą wysokość na trójwymiarowej powierzchni na rysunku 2.1.
Krzywe obojętności są reprezentacją wysokości (poziomu użyteczności) na płaskiej powierzchni. W ten sposób są one analogiczne do linii konturowej na mapie topograficznej. Przenosząc trójwymiarowy wykres z powrotem do przestrzeni dwuwymiarowej – przestrzeni A, B – możemy pokazać linie konturowe/krzywe obojętności, które reprezentują różne wysokości lub poziomy użyteczności. Na wykresie na rysunku 2.1 widać już, że ta funkcja użyteczności daje krzywe obojętności, które są „wygięte w łuk” lub wklęsłe względem początku.
Krzywe obojętności wynikają więc bezpośrednio z funkcji użyteczności i są użytecznym sposobem przedstawienia funkcji użyteczności na wykresie dwuwymiarowym.
2.4 Znajdowanie użyteczności krańcowej i krańcowej stopy substytucji
LO4: Wyznaczamy użyteczność krańcową i MRS dla typowych funkcji użyteczności.
Użyteczność krańcowa to dodatkowa użyteczność, jaką konsument otrzymuje z konsumpcji jednej dodatkowej jednostki dobra. Matematycznie wyrażamy to w następujący sposób:
MU_{a}= {frac{delta A}
lub zmiana użyteczności wynikająca ze zmiany ilości konsumowanego dobra A, gdzie Δ reprezentuje zmianę wartości dobra. Tak więc,
MU_{a}=(A+delta A,B)-U(A,B)}{delta A}
Zauważmy, że gdy badamy użyteczność krańcową konsumpcji A, utrzymujemy stałą wartość B.
Korzystając z rachunku, użyteczność krańcowa jest tym samym, co pochodna cząstkowa funkcji użyteczności względem A:
MU_{A}}frac{częściowa U(A,B)}{częściowa A}
Rozważmy konsumenta, który zasiada do posiłku składającego się z sałatki i pizzy. Załóżmy, że utrzymujemy ilość sałatki na stałym poziomie – na przykład jedna sałatka do obiadu. Teraz zwiększmy ilość plasterków pizzy, załóżmy, że przy 1 plasterku użyteczność wynosi 10, przy 2 wynosi 18, przy 3 wynosi 24, a przy 4 wynosi 28. Wykreślmy te liczby na wykresie, na którym użyteczność jest na osi pionowej, a pizza na osi poziomej (rysunek 2.2).
Rysunek 2.2: Wykres i tabela malejącej użyteczności krańcowej
|
Pizza Slices |
Utility |
Marginal Utility |
Marginal Użyteczność |
|
1 |
10 |
|
|
|
2 |
18 |
8 |
|
|
3 |
24 |
6 |
|
|
4 |
28 |
4 |
|
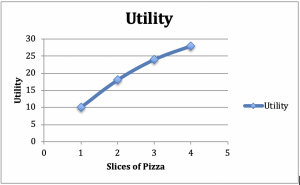
Z dodatniego nachylenia wykresu, możemy zaobserwować wzrost użyteczności wynikający z dodatkowych kawałków pizzy. Na podstawie wklęsłego kształtu wykresu możemy zaobserwować inne powszechne zjawisko: Dodatkowa użyteczność, którą konsument otrzymuje z każdego dodatkowego kawałka pizzy, maleje wraz z liczbą zjedzonych plasterków.
Fakt, że dodatkowa użyteczność staje się mniejsza z każdym dodatkowym kawałkiem pizzy, nazywamy zasadą malejącej użyteczności krańcowej. Zasada ta ma zastosowanie do dobrze zachowanych preferencji, w których preferowane są pakiety mieszane.
Marginalna stopa substytucji (MRS) to ilość jednego dobra, z którego konsument jest skłonny zrezygnować, aby uzyskać jedną jednostkę więcej innego dobra. Dlatego jest to to samo, co nachylenie krzywej obojętności – ponieważ utrzymujemy stały poziom satysfakcji, pozostajemy na tej samej krzywej obojętności, przesuwając się po niej tylko w miarę wymiany jednego dobra na drugie. How much of one you are willing to trade for one more of another depends on the marginal utility from each.
Using our previous example, if by consuming one more side salad your utility goes up by 10, then at a current consumption of 4 slices of pizza, you could give up 2 slices of pizza and go from 28 to 18 utils. 10 więcej utils z sałatki i 10 mniej utils przez rezygnację z 2 plasterków pizzy pozostawia ogólną użyteczność bez zmian – zatem nadal musimy znajdować się na tej samej krzywej obojętności. Poruszając się wzdłuż krzywej obojętności, musimy jechać po zboczu, to znaczy musimy rezygnować z dobra na osi pionowej na rzecz większej ilości dobra na osi poziomej, co daje ujemny wzrost przy dodatnim przebiegu.
Możemy przejść bezpośrednio od użyteczności krańcowej do MRS, rozpoznając związek między tymi dwoma pojęciami. W naszym przypadku, dla funkcji użyteczności U=U(A,B) , MRS przedstawia się następująco:
MRS=-odchylenie{MU_{A}}{MU_{B}}}
Zauważmy, że po podstawieniu możemy uprościć równanie:
MRS=- ______________________________}{ _______________________________ U(A,B)}}{ _______________________________ U(A,B)}
2.5 Pytanie dotyczące polityki
W module 1 ustaliliśmy, że odpowiednia decyzja konsumenta między większą liczbą przejechanych mil a inną konsumpcją prawdopodobnie odpowiada standardowym założeniom dotyczącym wyboru konsumenta. Dlatego użycie funkcji użyteczności Cobba-Douglasa do reprezentowania konsumenta, który lubi jeździć samochodem, jak również konsumować inne dobra, i który postrzega je jako kompromis (pieniądze wydane na gaz to pieniądze nie wydane na inne dobra konsumpcyjne), jest dobrym wyborem. Ma on również zalety zarówno zgodności z założeniami, jak i elastyczności:
U(MD,C)=MD^{a}C^{beta } gdzie MD = Przejechane mile, a C = Inna konsumpcja.
W rzeczywistości, sama funkcja może być przeniesiona do danych rzeczywistych, gdzie parametry i mogą być oszacowane dla tego rynku, rynku przejechanych mil w samochodzie konsumenta.
Rysunek 2.3 Wykres krzywych obojętności dla przykładu polityki
Przeanalizowanie pytań dotyczących polityki:
1 . Czy inne typy preferencji byłyby bardziej odpowiednie w tym przykładzie?
2. Co musiałoby być prawdą, aby doskonałe uzupełnienia były odpowiednim typem preferencji do wykorzystania w analizie tej polityki?
Co musiałoby być prawdą dla doskonałych substytutów? Biorąc pod uwagę, że rozważamy „typowego” konsumenta, który prowadzi samochód, czy właściwe jest wybranie „typowej” funkcji użyteczności?
4. Czy tylko zgadujemy, czy też mamy jakieś podstawy teoretyczne na poparcie naszego wyboru „dobrze zachowujących się” preferencji lub funkcji użyteczności Cobba-Douglasa?
PODSUMOWANIE
Przegląd: Topics and Related Learning Outcomes
2.1 Funkcje użyteczności
LO 2.1: Opisać funkcję użyteczności
2.2 Funkcje użyteczności i typowe preferencje
LO 2.2: Identyfikowanie funkcji użyteczności na podstawie typowych preferencji, które reprezentują
2.3 Odnoszenie funkcji użyteczności i map krzywych obojętności
LO 2.3: Wyjaśnić, jak wyprowadzić krzywą obojętności z funkcji użyteczności
2.4 Znajdowanie użyteczności krańcowej i krańcowej stopy substytucji
LO 2.4: Wyznaczyć użyteczność krańcową i krańcową stopę substytucji dla typowych funkcji użyteczności
2.5. Pytanie dotyczące polityki
Ucz się: Kluczowe pojęcia i wykresy
Bi.variate functions
Kardynalna
Linia konturowa
Zmniejszająca się użyteczność krańcowa
Funkcja
Marginalna stopa substytucji (MRS)
Użyteczność krańcowa
.
Ordinal
Funkcje jednowymiarowe
Util
Funkcja użyteczności
Funkcja użyteczności
Grafy
3D funkcja użyteczności i linia konturowa
Rozliczenia
Cobb-Douglas
Doskonałe uzupełnienia
Doskonałe substytuty
.