MezopotamiiEdit
W okresie 2700-2300 p.n.e. po raz pierwszy pojawiło się sumeryjskie liczydło, stół z kolejnymi kolumnami, które wyznaczały kolejne rzędy wielkości ich systemu liczbowego sexagesimal.
Niektórzy uczeni wskazują na znak w babilońskim piśmie klinowym, który mógł pochodzić z przedstawienia liczydła. It is the belief of Old Babylonian scholars such as Carruccio that Old Babylonians „may have used the abacus for the operations of addition and subtraction; however, this primitive device proved difficult to use for more complex calculations”.
EgyptianEdit
Użycie liczydła w starożytnym Egipcie jest wspomniane przez greckiego historyka Herodota, który pisze, że Egipcjanie manipulowali kamykami od prawej do lewej, w kierunku przeciwnym do greckiej metody od lewej do prawej. Archeolodzy znaleźli starożytne tarcze o różnych rozmiarach, które, jak się uważa, były używane jako liczmany. Nie odkryto jednak ściennych przedstawień tego instrumentu.
PerskiEdit
Podczas imperium Achemenidów, około 600 r. p.n.e., Persowie po raz pierwszy zaczęli używać liczydła. W czasach imperiów Partów, Sasanidów i Iranu uczeni koncentrowali się na wymianie wiedzy i wynalazków z otaczającymi ich krajami – Indiami, Chinami i Imperium Rzymskim, kiedy to, jak się uważa, były one eksportowane do innych krajów.
GreekEdit
Najwcześniejsze archeologiczne dowody na użycie greckiego liczydła datuje się na V wiek p.n.e. Również Demostenes (384 p.n.e.-322 p.n.e.) mówił o konieczności używania kamyków do obliczeń zbyt trudnych dla głowy. W sztuce Aleksego z IV w. p.n.e. wspomina się o liczydle i kamykach do księgowania, a zarówno Diogenes, jak i Polibiusz wspominają o mężczyznach, którzy czasem stali za więcej, a czasem za mniej, jak kamyki na liczydle. Greckie liczydło było stołem z drewna lub marmuru, wstępnie ustawionym z małymi licznikami z drewna lub metalu do obliczeń matematycznych. To greckie liczydło było używane w Persji Achemenidów, cywilizacji etruskiej, starożytnym Rzymie i, aż do Rewolucji Francuskiej, w zachodnim świecie chrześcijańskim.
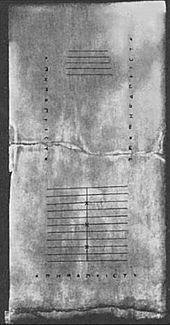
Tablica znaleziona na greckiej wyspie Salamis w 1846 r. (Tablica Salamis), pochodzi z 300 r. p.n.e., co czyni ją najstarszą tablicą liczącą odkrytą do tej pory. Jest to płyta z białego marmuru o długości 149 cm (59 cali), szerokości 75 cm (30 cali) i grubości 4,5 cm (2 cali), na której znajduje się 5 grup znaków. W centrum tablicy znajduje się zestaw 5 równoległych linii równo podzielonych linią pionową, zwieńczonych półkolem na przecięciu najniższej linii poziomej i pojedynczej linii pionowej. Pod tymi liniami znajduje się szeroka przestrzeń z poziomym pęknięciem dzielącym ją. Poniżej tego pęknięcia jest inna grupa jedenastu równoległych linii, ponownie podzielonych na dwie części przez linię prostopadłą do nich, ale z półkolem na szczycie przecięcia; trzecia, szósta i dziewiąta z tych linii są oznaczone krzyżykiem, gdzie przecinają się z linią pionową. Również z tego okresu pochodzi Waza Dariusa, która została odkopana w 1851 roku. To było pokryte z obrazami, w tym „skarbnik” trzymając tablet wosku w jednej ręce podczas manipulowania liczniki na stole z drugim.
ChineseEdit

| Abakus | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Tradycyjny chiński | 算盤 | |||||||||||||||
| Uproszczony chiński | 算盘 | |||||||||||||||
| Literalne znaczenie | „taca kalkulacyjna” | |||||||||||||||
| Tłumaczenia | Standardowe mandaryńskie | Hanyu Pinyin | IPA | Yue: Cantonese | Yale Romanization | Jyutping | IPA | Southern Min | Hokkien POJ | Tâi-lô | ||||||
Najwcześniejsza znana pisemna dokumentacja chińskiego liczydła pochodzi z II wieku p.n.e.
Chińskie liczydło, znane jako suanpan (算盤/算盘, lit. „taca do liczenia”), ma zazwyczaj 20 cm (8 cali) wysokości i występuje w różnych szerokościach, w zależności od operatora. Zazwyczaj ma więcej niż siedem prętów. Na każdym pręcie w górnej części znajdują się dwa koraliki, a w dolnej po pięć. Koraliki są zazwyczaj zaokrąglone i wykonane z twardego drewna. Koraliki są liczone poprzez przesuwanie ich w górę lub w dół w kierunku belki; koraliki przesunięte w kierunku belki są liczone, podczas gdy te przesunięte z dala od niej nie są liczone. Jeden z górnych koralików jest 5, podczas gdy jeden z dolnych koralików jest 1. Każdy pręt ma numer pod nim, pokazując wartość place.The suanpan może być zresetowany do pozycji wyjściowej natychmiast przez szybki ruch wzdłuż osi poziomej, aby obrócić wszystkie koraliki od poziomej belki w centrum.
Prototyp chińskiego liczydła pojawił się podczas dynastii Han, a koraliki są owalne. Dynastia Song i wcześniej używane 1:4 typu lub cztery-beads abakus podobne do nowoczesnego liczydła w tym kształt koralików powszechnie znany jako japoński stylu abacus.
W początkach dynastii Ming, liczydła zaczęły pojawiać się w postaci 1:5 abakus. Górny pokład miał jeden koralik i na dole miał pięć koralików.
W późnej dynastii Ming, style abakus pojawiły się w postaci 2:5. Górny pokład miał dwa koraliki, a dolny miał pięć koralików.
Różne techniki obliczeniowe zostały opracowane dla Suanpan umożliwiając skuteczne obliczenia. Obecnie istnieją szkoły uczące studentów, jak z niego korzystać.
W długim zwoju Along the River During the Qingming Festival namalowanym przez Zhang Zeduana w czasach dynastii Song (960-1297), suanpan jest wyraźnie widoczny obok księgi rachunkowej i recept lekarskich na ladzie apteki (Feibao).
Podobieństwo rzymskiego liczydła do chińskiego sugeruje, że jedno mogło zainspirować drugie, ponieważ istnieją pewne dowody na istnienie stosunków handlowych między Cesarstwem Rzymskim a Chinami. Jednakże nie można wykazać bezpośredniego związku, a podobieństwo liczydeł może być przypadkowe, oba ostatecznie powstały w wyniku liczenia z pięcioma palcami u ręki. Podczas gdy model rzymski (jak większość współczesnych koreańskich i japońskich) ma 4 plus 1 koralik na miejsce dziesiętne, standardowy suanpan ma 5 plus 2. Nawiasem mówiąc, pozwala to na użycie szesnastkowego systemu liczbowego (lub dowolnej bazy do 18), który mógł być używany w tradycyjnych chińskich miarach wagi. (Zamiast biegać na drutach, jak w chińskich, koreańskich i japońskich modelach, koraliki rzymskiego modelu biegną w rowkach, przypuszczalnie czyniąc obliczenia arytmetyczne znacznie wolniejszymi.
Innym możliwym źródłem suanpan są chińskie pręty do liczenia, które działały w systemie dziesiętnym, ale nie posiadały koncepcji zera jako uchwytu miejsca. Zero zostało prawdopodobnie wprowadzone do Chin w dynastii Tang (618-907), kiedy podróże po Oceanie Indyjskim i Bliskim Wschodzie zapewniłyby bezpośredni kontakt z Indiami, umożliwiając im nabycie koncepcji zera i przecinka dziesiętnego od indyjskich kupców i matematyków.
RomanEdit

Zwykła metoda obliczeń w starożytnym Rzymie, podobnie jak w Grecji, polegała na przesuwaniu liczmanów na gładkim stole. Pierwotnie używano do tego celu kamyków (calculi). Później, w średniowiecznej Europie, zaczęto produkować jetony. Zaznaczone linie wskazywały jednostki, piątki, dziesiątki itd. jak w rzymskim systemie liczbowym. Ten system „odlewania liczmanów” był kontynuowany w późnym Cesarstwie Rzymskim i w średniowiecznej Europie, a w ograniczonym zakresie był stosowany do XIX wieku. Dzięki ponownemu wprowadzeniu liczydła przez papieża Sylwestra II z modyfikacjami, stało się ono ponownie powszechnie używane w Europie w XI wieku. W liczydle tym używano koralików na drutach, w przeciwieństwie do tradycyjnych rzymskich tablic liczących, co oznaczało, że liczydło mogło być używane znacznie szybciej.
Piszący w I wieku p.n.e. Horacy wspomina o liczydle woskowym, tablicy pokrytej cienką warstwą czarnego wosku, na której za pomocą rylca wypisywano kolumny i cyfry.
Jeden przykład archeologicznego dowodu istnienia rzymskiego liczydła, pokazany tutaj w rekonstrukcji, pochodzi z I wieku n.e. Ma ono osiem długich rowków, w których mieszczą się cyfry. Ma ono osiem długich rowków zawierających do pięciu koralików w każdym i osiem krótszych rowków zawierających jeden lub zero koralików w każdym. Rowek oznaczony I oznacza jednostki, X dziesiątki, i tak dalej aż do milionów. Koraliki w krótszych rowkach oznaczają piątki – pięć jednostek, pięć dziesiątek itd., zasadniczo w dwójkowym kodowanym systemie dziesiętnym, związanym z cyframi rzymskimi. Krótkie rowki po prawej stronie mogły służyć do oznaczania rzymskich „uncji” (czyli ułamków).
IndianEdit
The Abhidharmakośabhāṣya of Vasubandhu (316-396), sanskryckie dzieło na temat filozofii buddyjskiej, mówi, że filozof Vasumitra z II wieku CE powiedział, że „umieszczenie knota (sanskryt vartikā) na liczbie jeden (ekāṅka) oznacza, że jest to jedynka, podczas gdy umieszczenie knota na liczbie sto oznacza, że jest on nazywany setką, a na liczbie tysiąc oznacza, że jest to tysiąc”. Nie jest jasne, na czym dokładnie mógł polegać ten układ. Około V wieku indyjscy urzędnicy znajdowali już nowe sposoby zapisywania zawartości abakusa. W hinduskich tekstach używano terminu śūnya (zero) na oznaczenie pustej kolumny na liczydle.
JapaneseEdit

W języku japońskim liczydło nazywa się soroban (算盤, そろばん, lit. „Taca do liczenia”), sprowadzone z Chin w XIV wieku. Prawdopodobnie było w użyciu przez klasę robotniczą na wiek lub więcej przed pojawieniem się klasy rządzącej, ponieważ struktura klasowa nie pozwalała, aby urządzenia używane przez klasę niższą były adoptowane lub używane przez klasę rządzącą. Liczydło 1/4, które usuwa rzadko używany drugi i piąty koralik stało się popularne w latach czterdziestych XX wieku.
Dzisiejsze japońskie liczydło jest typu 1:4, czteropiórkowe liczydło zostało wprowadzone z Chin w epoce Muromachi. Przyjmuje ono formę górnego pokładu jednego koralika i dolnego czterech koralików. Górny koralik na górnym pokładzie był równy pięciu i dolny jeden jest równy jeden jak chiński lub koreański liczydła, a liczba dziesiętna może być wyrażona, więc liczydło jest zaprojektowany jako jeden cztery liczydła. Koraliki są zawsze w kształcie rombu. Podział ilorazu jest zwykle używany zamiast metody podziału; w tym samym czasie, aby cyfry mnożenia i podziału konsekwentnie używać mnożenia podziału. Później w Japonii pojawiło się liczydło 3:5 o nazwie 天三算盤, które obecnie znajduje się w kolekcji Ize Rongji w Shansi Village w mieście Yamagata. Istniały również liczydła typu 2:5.
Wraz z rozprzestrzenianiem się liczydła czteropiórkowego, powszechne jest również używanie japońskich liczydeł na całym świecie. Istnieją również ulepszone japońskie liczydła w różnych miejscach. Jednym z japońskich liczydeł wyprodukowanych w Chinach jest plastikowe liczydło z aluminiową ramą. Plik znajduje się obok czterech koralików, a przycisk „kasowanie”, naciśnij przycisk kasowania, natychmiast umieścić górny koralik do górnej pozycji, dolny koralik jest wybierany do dolnej pozycji, natychmiast kasowanie, łatwe w użyciu.
Liczydło jest nadal produkowane w Japonii dzisiaj, nawet przy rozprzestrzenianiu się, praktyczności i przystępności kieszonkowych kalkulatorów elektronicznych. Posługiwanie się sorobanem jest nadal nauczane w japońskich szkołach podstawowych jako część matematyki, głównie jako pomoc w szybszym wykonywaniu obliczeń umysłowych. Wykorzystując wizualne wyobrażenie sorobanu, można dojść do odpowiedzi w tym samym czasie, a nawet szybciej, niż jest to możliwe przy użyciu fizycznego instrumentu.
KoreanEdit
Chińskie liczydło wyemigrowało z Chin do Korei około 1400 roku naszej ery. Koreańczycy nazywają je jupan (주판), supan (수판) lub jusan (주산).Cztery koraliki liczydła (1:4) zostały wprowadzone do Korei dynastii Goryeo z Chin podczas dynastii Song, później pięć koralików liczydła (5:1) liczydła zostało wprowadzone do Korei z Chin podczas dynastii Ming.
Native AmericanEdit


Niektóre źródła wspominają o użyciu liczydła zwanego nepohualtzintzin w starożytnej kulturze azteckiej. To mezoamerykańskie liczydło używało 5-cio cyfrowego systemu bazowego 20.Słowo Nepōhualtzintzin pochodzi z języka Nahuatl i jest utworzone przez korzenie; Ne – osobisty -; pōhual lub pōhualli – rachunek -; oraz tzintzin – małe podobne elementy. Jego pełne znaczenie zostało przyjęte jako: liczenie z małymi podobnymi elementami przez kogoś. Jego używania uczono w Calmecac temalpouhqueh , którzy byli uczniami przeznaczonymi do rachowania nieba, od dzieciństwa.
Nepōhualtzintzin dzielił się na dwie główne części oddzielone prętem lub sznurem pośrednim. W lewej części znajdowały się cztery paciorki, które w pierwszym rzędzie mają wartości jednostkowe (1, 2, 3, i 4), a w prawej trzy paciorki o wartościach odpowiednio 5, 10, i 15. Aby poznać wartość poszczególnych paciorków górnych rzędów, wystarczy pomnożyć przez 20 (przez każdy rząd), wartość odpowiedniego konta w pierwszym rzędzie.
W sumie było 13 rzędów z 7 paciorkami w każdym, co dawało 91 paciorków w każdym Nepōhualtzintzin. Była to podstawowa liczba do zrozumienia, 7 razy 13, ścisły związek między zjawiskami naturalnymi, światem podziemnym i cyklami niebios. Jeden Nepōhualtzintzin (91) reprezentował liczbę dni, które trwa dana pora roku, dwa Nepōhualtzintzin (182) to liczba dni cyklu kukurydzy, od jej zasiewu do zbiorów, trzy Nepōhualtzintzin (273) to liczba dni ciąży dziecka, a cztery Nepōhualtzintzin (364) kończyły cykl i przybliżały rok (brakowało 11/4 dni). Po przełożeniu na współczesną arytmetykę komputerową, Nepōhualtzintzin równał się stopniowi od 10 do 18 w systemie zmiennoprzecinkowym, który obliczał wielkości gwiazdowe, jak również nieskończenie małe z absolutną precyzją, co oznaczało, że żadne zaokrąglenia nie były dozwolone.
Ponowne odkrycie Nepōhualtzintzin zawdzięczamy meksykańskiemu inżynierowi Davidowi Esparza Hidalgo, który w swoich wędrówkach po Meksyku znalazł różnorodne ryciny i malowidła tego instrumentu i zrekonstruował kilka z nich wykonanych w złocie, jadeicie, inkrustacjach z muszli itp. Znaleziono również bardzo stare Nepōhualtzintzin przypisywane kulturze Olmec, a nawet kilka bransoletek pochodzenia majańskiego, jak również różnorodność form i materiałów w innych kulturach.
George I. Sanchez, „Arithmetic in Maya”, Austin-Texas, 1961 znalazł inne liczydło o podstawie 5, podstawie 4 na półwyspie Jukatan, które również obliczało dane kalendarzowe. Było to liczydło palcowe, z jednej strony używane były cyfry 0, 1, 2, 3 i 4, a z drugiej 0, 1, 2 i 3. Zwróć uwagę na użycie zera na początku i na końcu obu cykli. Sanchez pracował z Sylvanusem Morleyem, notowanym Mayanist.
The quipu of the Incas was a system of colored knotted cords used to record numerical data, like advanced tally sticks – but not used to perform calculations. Obliczenia przeprowadzano za pomocą yupany (Quechua oznacza „narzędzie do liczenia”; patrz rysunek), która była nadal w użyciu po podboju Peru. Zasada działania yupany nie jest znana, ale w 2001 roku włoski matematyk Nicolino De Pasquale zaproponował wyjaśnienie matematycznej podstawy tych instrumentów. Porównując formę kilku yupan, naukowcy odkryli, że obliczenia opierały się na sekwencji Fibonacciego 1, 1, 2, 3, 5 i potęgach 10, 20 i 40 jako wartościach miejsc dla różnych pól w instrumencie. Użycie sekwencji Fibonacciego pozwoliłoby utrzymać liczbę ziaren w obrębie jednego pola na minimalnym poziomie.
RussianEdit

Rosyjskie liczydło, schoty (rosyjskie: счёты, liczba mnoga od rosyjskiego: счёт, liczenie), zwykle ma pojedynczą pochyłą talię, z dziesięcioma koralikami na każdym drucie (z wyjątkiem jednego drutu, zwykle umieszczonego w pobliżu użytkownika, z czterema koralikami dla ułamków ćwierćrublowych). Starsze modele mają jeszcze jeden drut z czterema koralikami dla ćwierćrublówek, które były bite do 1916 roku. Rosyjskie liczydło jest często używane pionowo, z każdym drutem od lewej do prawej, jak linie w książce. Druty są zazwyczaj wygięte tak, aby wybrzuszały się w górę w środku, aby utrzymać koraliki przypięte do jednej z dwóch stron. Jest on oczyszczony, gdy wszystkie koraliki są przesunięte w prawo. Podczas manipulacji, koraliki są przesuwane w lewo. Dla ułatwienia, środkowe 2 koraliki na każdym drucie (5. i 6. koralik) są zazwyczaj innego koloru niż pozostałe osiem koralików. Podobnie, lewy koralik na drucie tysięcznym (i milionowym, jeśli jest obecny) może mieć inny kolor.
Jako proste, tanie i niezawodne urządzenie, rosyjskie liczydło było w użyciu we wszystkich sklepach i na rynkach w całym byłym Związku Radzieckim, a korzystanie z niego było nauczane w większości szkół aż do lat 90-tych. Nawet wynaleziony w 1874 roku mechaniczny kalkulator, arytmometr Odhnera, nie zastąpił ich w Rosji; według Jakowa Perelmana, nawet w jego czasach niektórzy biznesmeni próbujący sprowadzić takie urządzenia do Imperium Rosyjskiego byli znani z tego, że poddawali się i odchodzili w rozpaczy po tym, jak pokazano im pracę wykwalifikowanego operatora liczydła. Podobnie masowa produkcja arytmometrów Feliksa od 1924 roku nie zmniejszyła znacząco ich zastosowania w Związku Radzieckim. Rosyjskie liczydło zaczęło tracić na popularności dopiero po rozpoczęciu w 1974 roku w Związku Radzieckim masowej produkcji mikrokalkulatorów. Obecnie jest ono uważane za archaizm i zostało wyparte przez kalkulator ręczny.
Rosyjskie liczydło zostało przywiezione do Francji około 1820 roku przez matematyka Jeana-Victora Ponceleta, który służył w armii Napoleona i był jeńcem wojennym w Rosji. Liczydło wyszło z użycia w Europie Zachodniej w XVI wieku wraz z upowszechnieniem się notacji dziesiętnej i metod algorytmicznych. Dla współczesnych Ponceletowi Francuzów było to coś nowego. Poncelet używał go nie do celów użytkowych, ale jako pomocy dydaktycznej i demonstracyjnej. Turcy i Ormianie również używali liczydeł podobnych do rosyjskiego schoty. Przez Turków był on nazywany coulba, a przez Ormian choreb.