A Concise Introduction to Logic

9.1 A historical example

Filozof David Hume (1711-1776) jest pamiętany jako genialny sceptyczny empirysta. Osoba jest sceptykiem na jakiś temat, jeśli zarówno ma bardzo surowe standardy dotyczące tego, co stanowi wiedzę na ten temat, jak i wierzy, że nie możemy spełnić tych surowych standardów. Empiryzm to pogląd, że wiedzę zdobywamy przede wszystkim poprzez doświadczenie, zwłaszcza doświadczenie naszych zmysłów. W swojej książce, An Inquiry Concerning Human Understanding, Hume określa swoje zasady dla wiedzy, a następnie radzi nam, aby oczyścić nasze biblioteki:

Gdy biegamy po bibliotekach, przekonani o tych zasadach, jakie spustoszenie musimy zrobić? Jeśli na przykład weźmiemy do ręki jakiś tom boskości lub metafizyki szkolnej, zapytajmy: Czy zawiera on jakieś abstrakcyjne rozumowanie dotyczące ilości lub liczby? Nie. Czy zawiera jakieś doświadczalne rozumowanie dotyczące materii faktu i istnienia? Czy zawiera jakieś abstrakcyjne rozumowanie dotyczące ilości lub liczby? Nie. Rzućmy ją zatem do ognia, gdyż nie może zawierać nic poza sofistyką i iluzją.

Hume uważał, że jedynymi źródłami wiedzy są logiczne lub matematyczne rozumowanie (które nazywa powyżej „abstrakcyjnym rozumowaniem dotyczącym ilości lub liczby”) lub doświadczenie zmysłowe („eksperymentalne rozumowanie dotyczące materii faktu i istnienia”). Hume argumentuje, że wszelkie twierdzenia nie oparte na jednej lub drugiej metodzie są bezwartościowe.

Możemy zrekonstruować argument Hume’a w następujący sposób. Załóżmy, że t jest jakimś tematem, o którym twierdzimy, że mamy wiedzę. Przypuśćmy, że nie uzyskaliśmy tej wiedzy z doświadczenia lub logiki. Pisząc po angielsku, możemy zrekonstruować jego argument w następujący sposób:

Posiadamy wiedzę o t wtedy i tylko wtedy, gdy nasze twierdzenia o t są poznane w rozumowaniu doświadczalnym lub w logice czy matematyce.

Naszych twierdzeń o t nie poznajemy z rozumowania doświadczalnego.

Naszych twierdzeń o t nie poznajemy z logiki ani matematyki.

Nie mamy wiedzy o t.

Co oznacza to wyrażenie „jeśli i tylko jeśli”? Filozofowie uważają, że ono, i kilka synonimicznych zwrotów, jest często używane w rozumowaniach. Pozostawiając „jeśli i tylko” niewyjaśnione na razie, możemy użyć następującego klucza tłumaczeniowego, aby zapisać argument w mieszance naszej logiki propozycjonalnej i języka angielskiego.

P: Mamy wiedzę o t.

Q: Nasze twierdzenia o t są poznane na drodze rozumowania eksperymentalnego.

R: Nasze twierdzenia o t uczymy się z logiki lub matematyki.

I tak mamy:

P jeżeli i tylko jeżeli (QvR)

¬Q

¬R

¬P

Naszym zadaniem jest dodanie do naszego języka logicznego odpowiednika „jeżeli i tylko jeżeli”. Następnie będziemy mogli ocenić to przeformułowanie argumentu Hume’a.

9.2 Dwuwarunek

Zanim wprowadzimy symbol będący synonimem „jeśli i tylko jeśli”, a następnie przedstawimy jego składnię i semantykę, powinniśmy zacząć od pewnej obserwacji. Zdanie takie jak „P if and only if Q” wydaje się być skróconą formą powiedzenia „P if Q i P only if Q”. Kiedy już to zauważymy, nie musimy próbować odkryć znaczenia „if and only if” używając naszego eksperckiego rozumienia języka angielskiego. Zamiast tego, możemy odkryć znaczenie „if and only if” używając naszych już rygorystycznych definicji „if”, „and”, i „only if”. Konkretnie, „P jeśli Q i P tylko jeśli Q” będzie przetłumaczone „((Q→P)^(P→Q))”. (Jeśli jest to dla Ciebie niejasne, wróć do rozdziału 2.2.) Teraz zróbmy tabelę prawdy dla tej formuły.

.

.

P	Q	(Q → P)	(P → Q)	((Q→P)^(P→Q))
T	T	T	T
T	F	T	F	T	F	F
F	T	F	T	F
F	F	T	T	T

Ustaliliśmy semantykę dla „jeśli i tylko jeśli”. Możemy teraz wprowadzić nowy symbol dla tego wyrażenia. Tradycyjnie używamy podwójnej strzałki, „↔”. Możemy teraz wyrazić składnię i semantykę „↔”.

Jeśli Φ i Ψ są zdaniami, to

(Φ↔Ψ)

jest zdaniem. Ten rodzaj zdań jest zwykle nazywany „dwuwarunkowym”.

Semantyka jest podana przez następującą tabelę prawdy.

.

.

Φ	Ψ	(Φ↔Ψ)
T	T	T
T	F	F
F	T	F
F	F	T

Jednym z przyjemnych rezultatów naszego rachunku dwuwarunkowości jest to, że pozwala on nam zwięźle wyjaśnić syntaktyczne pojęcie równoważności logicznej. Mówimy, że dwa zdania Φ i Ψ są „równoważne” lub „logicznie równoważne”, jeśli (Φ↔Ψ) jest twierdzeniem.

9.3 Alternatywne zwroty

W języku angielskim wydaje się, że istnieje kilka zwrotów, które zazwyczaj mają to samo znaczenie, co dwuwarunkowe. Każde z poniższych zdań można by przetłumaczyć jako (P↔Q).

P if and only if Q.

P just in case Q.

P is necessary and sufficient for Q.

P is equivalent to Q.

9.4 Rozumowanie z użyciem biconditional

Jak możemy rozumować używając biconditional? Na początku mogłoby się wydawać, że nie oferuje ona zbyt wielu wskazówek. Jeśli wiem, że (P↔Q), to wiem, że P i Q mają tę samą wartość prawdy, ale z samego tego zdania nie wiem, czy oba są prawdziwe czy fałszywe. Niemniej jednak, możemy skorzystać z semantyki dla dwuwarunkowości i zauważyć, że jeśli znamy wartość prawdy jednego ze zdań tworzących dwuwarunkowość, to możemy wyprowadzić wartość prawdy drugiego zdania. To sugeruje prosty zestaw reguł. W rzeczywistości będą to cztery reguły, ale zgrupujemy je pod jedną nazwą, „równoważność”:

i

i

i

A co jeśli zamiast tego próbujemy pokazać dwuwarunkowość? Tutaj możemy powrócić do spostrzeżenia, że dwuwarunkowość (Φ↔Ψ) jest równoważna ((Φ→Ψ)^(Ψ→Φ)). Jeśli moglibyśmy udowodnić zarówno (Φ→Ψ) jak i (Ψ→Φ), to będziemy wiedzieli, że (Φ↔Ψ) musi być prawdziwe.

Regułę tę możemy nazwać „dwuwarunkiem”. Ma ona następującą postać:

(Φ→Ψ)

(Ψ→Φ)

(Φ↔Ψ)

Oznacza to, że często, gdy naszym celem jest udowodnienie warunku dwuwarunkowego, podejmiemy się przeprowadzenia dwóch derywacji warunkowych, aby wyprowadzić dwa warunki, a następnie skorzystamy z reguły warunku dwuwarunkowego. Oznacza to, że wiele dowodów dwuwarunkowości ma następującą postać:

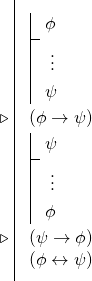
9.5 Powrót do Hume’a

Możemy teraz sprawdzić, czy jesteśmy w stanie udowodnić argument Hume’a. Biorąc pod uwagę nowy symbol dwuwarunkowy, możemy rozpocząć dowód bezpośredni z naszymi trzema przesłankami.

Zauważyliśmy już, że uważamy, iż (QvR) jest fałszywe, ponieważ ¬Q i ¬R. Udowodnijmy więc ¬(QvR). Tego zdania nie da się udowodnić bezpośrednio, biorąc pod uwagę przesłanki, którymi dysponujemy; nie da się go też udowodnić za pomocą dowodu warunkowego, gdyż nie jest ono warunkiem. Spróbujmy więc dowodu pośredniego. Wierzymy, że ¬(QvR) jest prawdziwe, więc założymy zaprzeczenie tego i wykażemy sprzeczność.

Targ Hume’a, przynajmniej tak jak go zrekonstruowaliśmy, jest ważny.

Czy argument Hume’a jest sensowny? To, czy jest on sensowny, zależy od pierwszej przesłanki powyżej (ponieważ druga i trzecia przesłanka są abstrakcjami na temat jakiegoś tematu t). W szczególności zależy to od twierdzenia, że posiadamy wiedzę o czymś tylko wtedy, gdy możemy to wykazać za pomocą eksperymentu lub logiki. Hume argumentuje, że powinniśmy nie ufać – wręcz powinniśmy spalić teksty zawierające twierdzenia, które nie pochodzą z eksperymentu i obserwacji, ani z logiki i matematyki. Rozważmy jednak to twierdzenie: posiadamy wiedzę o temacie t wtedy i tylko wtedy, gdy nasze twierdzenia o t są poznane na podstawie eksperymentu lub gdy nasze twierdzenia o t są poznane na podstawie logiki lub matematyki.

Czy Hume odkrył to twierdzenie poprzez eksperymenty? Czy też odkrył je za pomocą logiki? Jaki los spotkałby książkę Hume’a, gdybyśmy posłuchali jego rady?

9.6 Kilka przykładów

Pomocne może być udowodnienie pewnych twierdzeń, które korzystają z dwuwarunkowości, aby zilustrować, jak możemy rozumować z dwuwarunkowością.

Jest tu użyteczna zasada. Jeśli dwa zdania mają taką samą wartość prawdy jak trzecie zdanie, to mają taką samą wartość prawdy jak każde inne. Zapisujemy to jako (((P↔Q)^(R↔Q))→(P↔R)). Aby zilustrować rozumowanie dwuwarunkowe, udowodnijmy następujące twierdzenie.

Twierdzenie to jest twierdzeniem warunkowym, więc będzie wymagało wyprowadzenia warunkowego. Konsekwencja warunku jest dwuwarunkowa, więc będziemy oczekiwać, że będziemy potrzebować dwóch pochodnych warunkowych, jednej do udowodnienia (P→R) i jednej do udowodnienia (R→P). Dowód będzie wyglądał tak. Przestudiuj go dokładnie.

Wspominaliśmy wcześniej o zasadach, które kojarzymy z matematykiem Augustusem De Morganem (1806-1871), a które dziś nazywane są „Prawami De Morgana” lub „Równoważnościami De Morgana”. Są to uznania, że ¬(PvQ) i (¬P^¬Q) są równoważne, a także, że ¬(P^Q) i (¬Pv¬Q) są równoważne. Możemy je teraz wyrazić za pomocą dwuwarunkowości. Oto twierdzenia naszej logiki:

(¬(PvQ)↔(¬P^¬Q))

(¬(P^Q)↔(¬Pv¬Q))

Udowodnimy drugie z tych twierdzeń. Jest to być może najtrudniejszy dowód, jaki widzieliśmy; wymaga on zagnieżdżonych dowodów pośrednich i sporej dozy sprytu w znalezieniu odpowiedniej sprzeczności.

9.7 Wykorzystanie twierdzeń

Każde zdanie naszej logiki jest, w sensie semantycznym, jednego z trzech rodzajów. Jest ono albo tautologią, albo zdaniem sprzecznym, albo zdaniem warunkowym. Zdefiniowaliśmy już „tautologię” (zdanie, które musi być prawdziwe) i „zdanie sprzeczne” (zdanie, które musi być fałszywe). Zdanie warunkowe jest zdaniem, które nie jest ani tautologią, ani zdaniem sprzecznym. Tak więc, zdanie warunkowe jest zdaniem, które może być prawdziwe lub może być fałszywe.

Oto przykład każdego rodzaju zdania:

(Pv¬P)

(P↔¬P)

P

P

Pierwsze jest tautologią, drugie jest zdaniem sprzecznym, a trzecie jest zdaniem warunkowym. Możemy to zobaczyć na przykładzie tabeli prawdy.

.

P	¬P	(Pv¬P)	(P↔¬P)	P
T	F	T	F	T
F	T	T	F	F

Zauważmy, że negacja tautologii jest sprzecznością, negacja sprzeczności jest tautologią, a negacja zdania warunkowego jest zdaniem warunkowym.

¬(Pv¬P)

¬(P↔¬P)

¬P

.

.

P	¬P	(Pv¬P)	¬(Pv¬P)	(P↔¬P)	¬(P↔¬P)
T	F	T	F	F	T	T
F	T	T	F	F	T

Chwila zastanowienia ujawni, że byłoby to nie lada nieszczęściem, gdyby zdanie sprzeczne lub zdanie warunkowe było twierdzeniem naszej logiki propozycjonalnej. Nasza logika została zaprojektowana tak, by produkować tylko ważne argumenty. Zauważyliśmy, że argumenty, które nie mają przesłanek, powinny mieć wnioski, które muszą być prawdziwe (znowu, wynika to z tego, że zdanie, które może być udowodnione bez przesłanek, może być udowodnione z dowolnymi przesłankami, a więc lepiej, żeby było prawdziwe bez względu na to, jakich przesłanek użyjemy). Gdyby twierdzenie było wewnętrznie sprzeczne, wiedzielibyśmy, że możemy udowodnić fałsz. Jeśli twierdzenie byłoby warunkowe, to czasami moglibyśmy udowodnić fałsz (to znaczy, moglibyśmy udowodnić zdanie, które pod pewnymi warunkami jest fałszywe). A biorąc pod uwagę, że przyjęliśmy pośrednie wyprowadzanie jako metodę dowodu, wynika z tego, że gdy mamy sprzeczność lub zdanie sprzeczne w argumencie, możemy udowodnić wszystko.

Twierdzenia mogą być dla nas bardzo użyteczne w argumentacji. Załóżmy, że wiemy, że ani Smith, ani Jones nie pojadą do Londynu, i chcemy udowodnić, że Jones nie pojedzie do Londynu. Gdybyśmy pozwolili sobie na użycie jednego z twierdzeń De Morgana, moglibyśmy szybko rozprawić się z tym argumentem. Przyjmijmy następujący klucz:

P: Smith pojedzie do Londynu.

Q: Jones pojedzie do Londynu.

I mamy następujący argument:

Dowód ten stał się bardzo łatwy dzięki zastosowaniu przez nas twierdzenia w wierszu 2.

Należy tu zwrócić uwagę na dwie rzeczy. Po pierwsze, powinniśmy sobie na to pozwolić, bo jeśli wiemy, że jakieś zdanie jest twierdzeniem, to wiemy, że możemy to twierdzenie udowodnić w pod-dowodzie. To znaczy, moglibyśmy zastąpić linię 2 powyżej długim subdowodem, który udowadnia (¬(P v Q)↔(¬P ^ ¬Q)), którego moglibyśmy następnie użyć. Ale jeśli jesteśmy pewni, że (¬(P v Q)↔(¬P ^ ¬Q)) jest twierdzeniem, nie powinniśmy potrzebować przeprowadzać tego dowodu ponownie i ponownie, za każdym razem, gdy chcemy skorzystać z tego twierdzenia.

Drugi problem, który powinniśmy rozpoznać jest bardziej subtelny. Istnieje nieskończenie wiele zdań w formie naszego twierdzenia i powinniśmy być w stanie wykorzystać je również. Na przykład, następujące zdania miałyby dowód identyczny z naszym dowodem twierdzenia (¬(P v Q)↔(¬P ^ ¬Q)), z tą różnicą, że litery byłyby inne:

(¬(R v S) ↔ (¬R ^ ¬S))

(¬(T v U) ↔ (¬T ^ ¬U))

(¬(V v W) ↔ (¬V ^ ¬W))

Jest to, miejmy nadzieję, oczywiste. Weźmy dowód (¬(P v Q)↔(¬P ^ ¬Q)), i w tym dowodzie zastąpmy każdą instancję P przez R i każdą instancję Q przez S, a będziemy mieli dowód (¬(R v S)↔(¬R ^ ¬S)).

Ale jest coś, co być może jest mniej oczywiste. Każde z poniższych twierdzeń można uważać za podobne do twierdzenia (¬(P v Q)↔(¬P ^ ¬Q)).

(¬((P^Q) v (R^S))↔(¬(P^Q) ^ ¬(R^S)))

(¬(T v (Q v V))↔(¬T ^ ¬(Q v V)))

(¬((Q↔P) v (¬R→¬Q))↔(¬(Q↔P) ^ ¬(¬R→¬Q)))

Na przykład, jeśli weźmiemy dowód (¬(P v Q)↔(¬P ^ ¬Q)) i zastąpimy każdą początkową instancję P przez (Q↔P) oraz każdą początkową instancję Q przez (¬R→¬Q), to otrzymalibyśmy dowód twierdzenia (¬((Q↔P) v (¬R→¬Q))↔(¬(Q↔P) ^ ¬(¬R→¬Q))).

Możemy uchwycić ten wgląd na dwa sposoby. Moglibyśmy podać twierdzenia naszego metajęzyka i pozwolić, by miały one swoje instancje. Tak więc, moglibyśmy wziąć (¬(Φ v Ψ) ↔ (¬Φ ^ ¬Ψ)) jako twierdzenie metajęzyka, w którym moglibyśmy zastąpić każde Φ zdaniem i każde Ψ zdaniem i otrzymać konkretną instancję twierdzenia. Alternatywą jest pozwolenie, by z danego twierdzenia można było wyprodukować inne twierdzenia przez podstawienie. Dla ułatwienia przyjmiemy tę drugą strategię.

Nasza reguła będzie następująca. Gdy raz udowodnimy jakieś twierdzenie, możemy się na nie powołać w dowodzie w każdej chwili. Naszym uzasadnieniem jest to, że twierdzenie jest twierdzeniem. Zezwalamy na zastąpienie dowolnego zdania atomowego w twierdzeniu dowolnym innym zdaniem wtedy i tylko wtedy, gdy każdą początkową instancję tego zdania atomowego w twierdzeniu zastąpimy tym samym zdaniem.

Zanim rozważymy przykład, korzystnie jest wymienić kilka użytecznych twierdzeń. Istnieje nieskończenie wiele twierdzeń naszego języka, ale te dziesięć jest często bardzo pomocne. Kilka z nich już udowodniliśmy. Pozostałe można udowodnić w ramach ćwiczenia.

T1 (P v ¬P)

T2 (¬(P→Q) ↔ (P^¬Q))

T3 (¬(P v Q) ↔ (¬P ^ ¬Q))

T4 ((¬P v ¬Q) ↔ ¬(P ^ Q))

T5 (¬(P ↔ Q) ↔ (P ↔ ¬Q))

T6 (¬P → (P → Q))

T7 (P → (Q → P))

T8 ((P→(Q→R)) → ((P→Q) → (P→R)))

T9 ((¬P→¬Q) → ((¬P→Q) →P))

T10 ((P→Q) → (¬Q→¬P))

Niektóre przykłady uświadomią nam zaletę stosowania twierdzeń. Rozważmy inny argument, bazujący na powyższym. Wiemy, że ani nie jest tak, że jeśli Smith pojedzie do Londynu, to pojedzie do Berlina, ani nie jest tak, że jeśli Jones pojedzie do Londynu, to pojedzie do Berlina. Chcemy udowodnić, że nie jest tak, że Jones pojedzie do Berlina. Do naszego klucza dodajemy:

R: Smith pojedzie do Berlina.

S: Jones pojedzie do Berlina.

I mamy następujący argument:

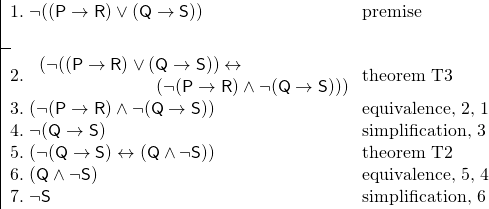
Użycie twierdzeń uczyniło ten dowód znacznie krótszym niż mógłby być w innym przypadku. Ponadto, twierdzenia często ułatwiają śledzenie dowodu, ponieważ rozpoznajemy twierdzenia jako tautologie – jako zdania, które muszą być prawdziwe.

9.8 Problemy

1. Wykaż, że każdy z poniższych argumentów jest ważny.

1. Premienie: P, ¬Q. Konkluzja: ¬(P↔Q).
2. Preferencje: (¬PvQ), (Pv¬Q). Wnioskowanie: (P↔Q).
3. Preferencje: (P↔Q), (R↔S) . Wniosek: ((P^R)↔(Q^S)).

1. Dowiedz się każdego z następujących twierdzeń.

1. T1
2. T2
3. T5
4. T6
5. T7
6. T8
7. T9
8. ((P^Q)↔¬(¬Pv¬Q))
9. ((P→Q)↔¬(P^¬Q))

1. W normalnym potocznym angielskim, napisz swój własny poprawny argument z co najmniej dwoma przesłankami, z których co najmniej jedna jest dwuwarunkowa. Twój argument powinien być po prostu akapitem (nie uporządkowaną listą zdań ani niczym innym, co wygląda jak logika formalna). Przetłumacz go na logikę propozycjonalną i udowodnij, że jest ważny.
2. W normalnym potocznym angielskim, napisz swój własny ważny argument z co najmniej dwoma przesłankami i z wnioskiem, który jest dwuwarunkowy. Twój argument powinien być po prostu akapitem (nie uporządkowaną listą zdań lub czymkolwiek innym, co wygląda formalnie jak logika). Przetłumacz go na logikę propozycjonalną i udowodnij, że jest ważny.

.