In het moderne audiotijdperk kun je niet meer heen om de vermelding van “Hi-Res” en 24-bit “Studio Quality” muziek. Als je de trend niet hebt opgemerkt in high-end smartphones – Sony’s LDAC Bluetooth codec – en streamingdiensten zoals Tidal, dan moet je echt beginnen met het lezen van deze site meer.
De belofte is eenvoudig – superieure luisterkwaliteit dankzij meer gegevens, aka bit-diepte. Dat is 24-bits van digitale enen en nullen tegenover de miezerige 16-bit kater uit het CD-tijdperk. Natuurlijk moet u extra betalen voor deze producten en diensten van hogere kwaliteit, maar meer bits zijn toch beter?
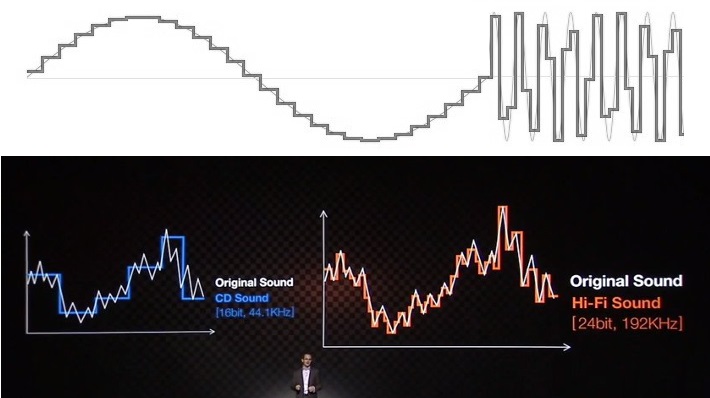
“Low res”-audio wordt vaak afgebeeld als een trapsgewijze golfvorm. Dit is niet hoe audio sampling werkt en het is ook niet hoe audio eruit ziet als het uit een apparaat komt.
Niet noodzakelijk. De behoefte aan steeds hogere bit-dieptes is niet gebaseerd op de wetenschappelijke werkelijkheid, maar eerder op een verdraaiing van de waarheid en het uitbuiten van een gebrek aan consumentenbewustzijn over de wetenschap van geluid. Uiteindelijk hebben bedrijven die 24-bit audio op de markt brengen veel meer aan winst dan aan superieure afspeelkwaliteit.
Bit-diepte en geluidskwaliteit: Traplopen is geen ding
Om te suggereren dat 24-bit audio een must-have is, draven bedrijven (en te veel anderen die dit onderwerp proberen uit te leggen) op met de zeer bekende audiokwaliteitstrap naar de hemel. Het 16-bit voorbeeld toont altijd een hobbelige, gekartelde weergave van een sinusgolf of ander signaal, terwijl het 24-bit equivalent er prachtig glad uitziet en een hogere resolutie heeft. Het is een eenvoudig visueel hulpmiddel, maar een dat berust op onwetendheid over het onderwerp en de wetenschap om consumenten tot de verkeerde conclusies te brengen.
Voordat iemand me de kop afbijt, technisch gesproken geven deze trapsgewijze voorbeelden wel een enigszins accuraat beeld van audio in het digitale domein. Echter, een stam plot / lolly grafiek is een meer accurate grafiek voor visuele audio sampling dan deze trap-stappen. Denk er eens zo over – een sample bevat een amplitude op een zeer specifiek tijdstip, niet een amplitude die gedurende een specifieke tijdsduur wordt vastgehouden.

Het gebruik van trapgrafieken is opzettelijk misleidend wanneer stamdiagrammen een nauwkeurigere weergave van digitale audio bieden. Deze twee grafieken plotten dezelfde gegevenspunten, maar de trapgrafiek lijkt veel minder nauwkeurig.
Het is echter juist dat een analoog naar digitaal omzetter (ADC) een oneindig analoog audiosignaal moet passen in een eindig aantal bits. Een bit dat tussen twee niveaus valt, moet worden afgerond tot de dichtstbijzijnde benadering, wat bekend staat als een kwantisatiefout of kwantisatieruis. (Onthoud dit, want we komen er nog op terug.)
Als je echter kijkt naar de audio-uitgang van een audio digitaal naar analoog omzetter (DAC) die deze eeuw is gebouwd (en waarschijnlijk al veel eerder), dan zie je geen traptreden. Zelfs niet als je een 8-bit signaal uitvoert. Wat is er dan?

Een 8-bits, 10 kHz sinusgolfuitvoer van een goedkope Pixel 3a-smartphone. We zien wat ruis, maar geen merkbare traptreden die zo vaak worden afgeschilderd door audiobedrijven.
First, wat deze traptrede-diagrammen beschrijven, als we ze toepassen op een audio-uitvoer, is iets dat een zero-order-hold DAC wordt genoemd. Dit is een zeer eenvoudige en goedkope DAC-technologie waarbij een signaal bij elke nieuwe sample tussen verschillende niveaus wordt geschakeld om een uitgang te geven. Dit wordt niet gebruikt in professionele of half-decente consumentenaudioproducten. Je vindt het misschien in een microcontroller van $5, maar zeker nergens anders. Een onjuiste voorstelling van audio-uitgangen op deze manier impliceert een vervormde, onnauwkeurige golfvorm, maar dit is niet wat u krijgt.

In werkelijkheid is de uitgang van een moderne ∆Σ DAC een oversampled 1-bit PDM-signaal (rechts), in plaats van een nul-vasthoudsignaal (links). Deze laatste produceert een analoge output met minder ruis wanneer deze wordt gefilterd.
Audio-grade ADC’s en DAC’s zijn hoofdzakelijk gebaseerd op delta-sigma (∆Σ) modulatie. Componenten van dit kaliber zijn onder meer interpolatie en oversampling, noise shaping, en filtering om ruis glad te strijken en te verminderen. Delta-sigma DAC’s zetten audiosamples om in een 1-bit stroom (pulsdichtheidsmodulatie) met een zeer hoge samplesnelheid. Wanneer dit wordt gefilterd, levert dit een vloeiend uitgangssignaal op waarbij ruis ver buiten de hoorbare frequenties wordt geduwd.
In een notendop: moderne DAC’s produceren geen ruw uitziende gekartelde audiosamples – zij produceren een bitstroom die op ruis is gefilterd tot een zeer nauwkeurige, vloeiende output. Deze trapsgewijze visualisatie is verkeerd vanwege iets dat “kwantiseringsruis” wordt genoemd.
Uitleg Kwantiseringsruis
In elk eindig systeem komen afrondingsfouten voor. Het is waar dat een 24-bit ADC of DAC een kleinere afrondingsfout zal hebben dan een 16-bit equivalent, maar wat betekent dat eigenlijk? Belangrijker nog, wat horen we eigenlijk? Is het vervorming of fuzz, gaan details voor altijd verloren?
Het is eigenlijk een beetje van allebei, afhankelijk van of je je in de digitale of analoge wereld bevindt. Maar het sleutelbegrip om beide te begrijpen is grip te krijgen op de ruisvloer, en hoe deze verbetert naarmate de bit-diepte toeneemt. Om dit te demonstreren, stappen we even af van 16 en 24 bits en kijken we naar voorbeelden met een zeer kleine bitdiepte.
Het verschil tussen 16 en 24 bitdiepten is niet de nauwkeurigheid in de vorm van een golfvorm, maar de beschikbare limiet voordat digitale ruis ons signaal verstoort.
Er zijn nogal wat dingen om te controleren in het onderstaande voorbeeld, dus eerst een korte uitleg van waar we naar kijken. We hebben onze ingangsgolfvormen (blauw) en gekwantiseerde (oranje) golfvormen in de bovenste grafieken, met bitdieptes van 2, 4 en 8 bits. We hebben ook een kleine hoeveelheid ruis aan ons signaal toegevoegd om de echte wereld beter te simuleren. Onderaan hebben we een grafiek van de kwantiseringsfout of afrondingsruis, die wordt berekend door het gekwantiseerde signaal af te trekken van het ingangssignaal.

Quantiseringsruis neemt toe naarmate de bitdiepte kleiner is, door afrondingsfouten.
Het vergroten van de bitdiepte maakt duidelijk dat het gekwantiseerde signaal beter overeenkomt met het ingangssignaal. Maar dat is niet wat belangrijk is, let op het veel grotere fout/ruis signaal voor de lagere bit-dieptes. Het gekwantiseerde signaal heeft geen data verwijderd uit ons ingangssignaal, het heeft in feite dat foutsignaal toegevoegd. Additieve synthese vertelt ons dat een signaal kan worden gereproduceerd door de som van twee andere signalen, met inbegrip van signalen die uit fase zijn en als aftrekking werken. Dat is hoe ruisonderdrukking werkt. Dus deze afrondingsfouten introduceren een nieuw ruis signaal.
Dit is niet alleen theoretisch, je kunt daadwerkelijk meer en meer ruis horen in audio bestanden met een lagere bit- diepte. Om te begrijpen waarom, onderzoekt u wat er gebeurt in het 2-bit voorbeeld met zeer kleine signalen, zoals vóór 0,2 seconden. Klik hier voor een ingezoomde grafiek. Zeer kleine veranderingen in het ingangssignaal veroorzaken grote veranderingen in de gekwantiseerde versie. Dit is de afrondingsfout in actie, die tot gevolg heeft dat ruis van kleine signalen wordt versterkt. Dus nogmaals, de ruis wordt luider naarmate de bit-diepte afneemt.
Kwantisering verwijdert geen gegevens uit onze invoer, maar voegt in feite een ruisachtig foutsignaal toe.
Denk hier ook eens andersom over: het is niet mogelijk een signaal vast te leggen dat kleiner is dan de grootte van de kwantiseringsstap – ironisch genoeg bekend als het minst significante bit. Kleine signaalveranderingen moeten overspringen naar het dichtstbijzijnde kwantiseringsniveau. Grotere bitdieptes hebben kleinere kwantisatiestappen en dus kleinere niveaus van ruisversterking.
Het belangrijkste is echter dat de amplitude van de kwantisatie-ruis consistent blijft, ongeacht de amplitude van de ingangssignalen. Dit toont aan dat ruis optreedt bij alle verschillende kwantiseringsniveaus, dus er is een consistent ruisniveau voor elke gegeven bit-diepte. Grotere bit-dieptes produceren minder ruis. We moeten daarom de verschillen tussen 16 en 24 bit-dieptes niet zien als de nauwkeurigheid in de vorm van een golfvorm, maar als de beschikbare limiet voordat digitale ruis ons signaal verstoort.
Bit-diepte heeft alles te maken met ruis
Nu we het over bit-diepte hebben in termen van ruis, gaan we nog een laatste keer terug naar onze bovenstaande grafiek. Merk op hoe het 8-bit voorbeeld een bijna perfecte overeenkomst lijkt te zijn voor ons ruisige ingangssignaal. Dat komt omdat de 8-bits resolutie in feite voldoende is om het niveau van de achtergrondruis vast te leggen. Met andere woorden: de kwantiseringsstapgrootte is kleiner dan de amplitude van de ruis, of de signaal-ruisverhouding (SNR) is beter dan het niveau van de achtergrondruis.
De vergelijking 20log(2n), waarbij n de bitdiepte is, geeft ons de SNR. Een 8-bits signaal heeft een SNR van 48dB, 12-bits is 72dB, terwijl 16-bits 96dB haalt, en 24-bits maar liefst 144dB. Dit is belangrijk omdat we nu weten dat we alleen een bit-diepte nodig hebben met voldoende SNR voor het dynamische bereik tussen onze achtergrondruis en het luidste signaal dat we willen opnemen om audio zo perfect weer te geven als het in de echte wereld verschijnt. Het wordt een beetje lastig om van de relatieve schalen van de digitale wereld over te stappen op de op geluidsdruk gebaseerde schalen van de fysieke wereld, dus we zullen proberen het eenvoudig te houden.
We hebben een bit-diepte nodig met voldoende SNR om ons achtergrondgeluid te accommoderen zodat we ons geluid zo perfect kunnen vastleggen als het in de echte wereld klinkt.
Jouw oor heeft een gevoeligheid die varieert van 0dB (stilte) tot ongeveer 120dB (pijnlijk hard geluid), en het typische vermogen om volumes te onderscheiden ligt slechts 1dB uit elkaar. Het dynamische bereik van uw oor is dus ongeveer 120dB, oftewel bijna 20-bits.
U kunt dit echter niet allemaal tegelijk horen, omdat het trommelvlies, of trommelvlies, zich vernauwt om de hoeveelheid volume die het binnenoor in luide omgevingen bereikt, te verminderen. U zult ook niet naar muziek luisteren die zo hard is, want dan wordt u doof. Bovendien zijn de omgevingen waarin jij en ik naar muziek luisteren niet zo stil als gezonde oren kunnen horen. Een goed behandelde opnamestudio brengt ons misschien onder de 20dB voor achtergrondlawaai, maar luisteren in een drukke huiskamer of in de bus zal de omstandigheden duidelijk verslechteren en onze behoefte aan een hoog dynamisch bereik verminderen.
Het menselijk oor heeft een enorm dynamisch bereik, maar alleen niet allemaal tegelijk. Maskering en gehoorbescherming verminderen de effectiviteit ervan.
Daar komt nog bij: naarmate de luidheid toeneemt, treedt maskering van hogere frequenties in uw oor op. Bij lage volumes van 20 tot 40 dB treedt er geen maskering op, behalve bij geluiden die dicht bij de toonhoogte liggen. Bij 80 dB worden geluiden onder 40 dB echter gemaskeerd, terwijl bij 100 dB geluiden onder 70 dB onmogelijk te horen zijn. De dynamische aard van het oor en het luistermateriaal maakt het moeilijk om een precies getal te geven, maar het werkelijke dynamische bereik van uw gehoor ligt waarschijnlijk in de buurt van 70 dB in een gemiddelde omgeving, tot slechts 40 dB in zeer luide omgevingen. Een bitdiepte van slechts 12 bits zou waarschijnlijk voor de meeste mensen voldoende zijn, zodat 16-bit CD’s ons voldoende speelruimte geven.

hyperfysicaHoge-frequentiemaskering treedt op bij luide volumes, waardoor onze waarneming van stillere geluiden wordt beperkt.
De meeste instrumenten en opnamemicrofoons introduceren ook ruis (vooral gitaarversterkers), zelfs in zeer stille opnamestudio’s. Er zijn ook een paar studies geweest naar het dynamisch bereik van verschillende genres, waaronder deze die een typisch dynamisch bereik van 60dB laat zien. Het zal geen verbazing wekken dat genres met een grotere affiniteit voor stille partijen, zoals koor, opera en piano, een maximaal dynamisch bereik hebben van rond de 70dB, terwijl “hardere” rock-, pop- en rapgenres neigen naar 60dB en lager. Uiteindelijk kan muziek maar met zoveel natuurgetrouwheid worden geproduceerd en opgenomen.
Je bent misschien ook bekend met de “loudness wars” van de muziekindustrie, die het doel van de huidige Hi-Res audioformaten zeker voorbijschieten. Zwaar gebruik van compressie (die ruis versterkt en pieken verzwakt) vermindert het dynamisch bereik. Moderne muziek heeft aanzienlijk minder dynamisch bereik dan albums van 30 jaar geleden. Theoretisch zou moderne muziek met lagere bit-rates kunnen worden gedistribueerd dan oude muziek. U kunt het dynamisch bereik van een groot aantal albums hier bekijken.

CD-kwaliteit mag dan “slechts” 16 bits zijn, maar het is overkill voor kwaliteit.
16 bits is alles wat u nodig hebt
Dit is een hele reis geweest, maar hopelijk hebt u een veel genuanceerder beeld gekregen van bitdiepte, ruis en dynamisch bereik dan de misleidende trap-trap-klasvoorbeelden die u zo vaak ziet.
Bit-diepte heeft alles te maken met ruis, en hoe meer bits je hebt om audio op te slaan: hoe minder kwantisatieruis er in je opname wordt geïntroduceerd. Op dezelfde manier kun je ook kleinere signalen nauwkeuriger vastleggen, waardoor de digitale ruisvloer onder de opname- of luisteromgeving wordt gebracht. Dat is alles waar we bitdiepte voor nodig hebben. Er is geen voordeel bij het gebruik van enorme bit-dieptes voor audio masters.
Verrassend genoeg is 12-bits waarschijnlijk genoeg voor een behoorlijk klinkende muziek master en om tegemoet te komen aan het dynamische bereik van de meeste luisteromgevingen. Digitale audio transporteert echter meer dan alleen muziek, en voorbeelden zoals spraak of omgevingsopnamen voor TV kunnen gebruik maken van een groter dynamisch bereik dan de meeste muziek doet. Bovendien kan een beetje headroom voor de scheiding tussen luid en zacht nooit kwaad.
Per saldo biedt 16 bits (96 dB dynamisch bereik of 120 dB met dithering toegepast) ruimte aan een breed scala van audiosoorten, alsmede aan de grenzen van het menselijk gehoor en typische luisteromgevingen. De perceptuele toename van 24-bits kwaliteit is zeer discutabel, zo niet gewoon een placebo, zoals ik hoop te hebben aangetoond. Bovendien maakt de toename van de bestandsgrootte en de bandbreedte ze overbodig. Het type compressie dat wordt gebruikt om de bestandsgrootte van uw muziekbibliotheek of -stream te verkleinen heeft een veel merkbaarder effect op de geluidskwaliteit dan de vraag of het een 16- of 24-bit bestand is.