MesopotamischEdit
In de periode 2700-2300 v.Chr. verscheen voor het eerst het telraam van Soemerië, een tabel met opeenvolgende kolommen die de opeenvolgende orden van grootte van hun sexagesimale getallenstelsel afbakenden.
Sommige geleerden wijzen op een teken in het Babylonische spijkerschrift dat kan zijn afgeleid van een weergave van het telraam. Oud-Babylonische geleerden zoals Carruccio zijn van mening dat de Oud-Babyloniërs “het telraam gebruikt kunnen hebben voor optellen en aftrekken; dit primitieve apparaat bleek echter moeilijk te gebruiken voor complexere berekeningen”.
EgyptianEdit
Het gebruik van het telraam in het Oude Egypte wordt vermeld door de Griekse historicus Herodotus, die schrijft dat de Egyptenaren de kiezelsteentjes van rechts naar links hanteerden, tegengesteld aan de Griekse van links naar rechts methode. Archeologen hebben in de oudheid schijven van verschillende afmetingen gevonden waarvan men denkt dat ze als tellers werden gebruikt. Er zijn echter geen muurafbeeldingen van dit instrument ontdekt.
PerzischEdit
Tijdens het Achaemenidenrijk, rond 600 v. Chr., begonnen de Perzen voor het eerst het telraam te gebruiken. Onder de Parthische, Sassanische en Iraanse rijken concentreerden de geleerden zich op het uitwisselen van kennis en uitvindingen met de landen om hen heen – India, China en het Romeinse Rijk, wanneer men denkt dat het naar andere landen werd geëxporteerd.
GrieksEdit
De vroegste archeologische bewijzen voor het gebruik van het Griekse telraam dateren uit de 5e eeuw v. Chr. Ook Demosthenes (384 v.Chr.-322 v.Chr.) sprak van de noodzaak om kiezelsteentjes te gebruiken voor berekeningen die te moeilijk voor het hoofd waren. Een toneelstuk van Alexis uit de 4e eeuw v.C. vermeldt een telraam en kiezelstenen voor de boekhouding, en zowel Diogenes als Polybius hebben het over mannen die soms voor meer en soms voor minder stonden, zoals de kiezelstenen op een telraam. Het Griekse telraam was een tafel van hout of marmer, vooraf ingesteld met kleine tellers in hout of metaal voor wiskundige berekeningen. Het Griekse telraam werd gebruikt in Achaemenidisch Perzië, de Etruskische beschaving, het Oude Rome en, tot aan de Franse Revolutie, in de Westerse Christelijke wereld.
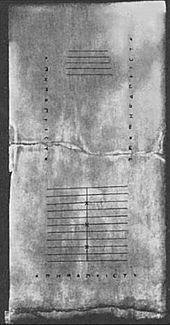
Een tablet dat in 1846 AD op het Griekse eiland Salamis werd gevonden (het Salamis Tablet), dateert uit 300 v. Chr. en is daarmee het oudste telbord dat tot nu toe is ontdekt. Het is een witte marmeren plaat van 149 cm lang, 75 cm breed en 4,5 cm dik, waarop 5 groepen tekens zijn aangebracht. In het midden van het tablet is een reeks van 5 parallelle lijnen gelijk verdeeld door een verticale lijn, bekroond met een halve cirkel op het snijpunt van de onderste horizontale lijn en de enkele verticale lijn. Onder deze lijnen is een brede ruimte met een horizontale barst die het doorsnijdt. Onder deze scheur is nog een groep van elf parallelle lijnen, weer in tweeën gedeeld door een lijn die loodrecht op hen staat, maar met de halve cirkel bovenaan het snijpunt; de derde, zesde en negende van deze lijnen zijn gemarkeerd met een kruis waar zij de verticale lijn snijden. Uit dit tijdperk stamt ook de Dariusvaas die in 1851 werd opgegraven. Hij was bedekt met afbeeldingen waaronder een “schatbewaarder” die in de ene hand een wastablet vasthoudt terwijl hij met de andere hand tellers op een tafel manipuleert.
ChineesEdit

| Abacus | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Traditioneel Chinees | 算盤 | |||||||||||||||
| Vereenvoudigd Chinees | 算盘 | |||||||||||||||
| Literal betekenis | “rekenblad” | |||||||||||||||
| Transcripties | Standaard Mandarijn | Hanyu Pinyin | IPA | Yue: Kantonees | Yale-romanisering | Jyutping | IPA | Southern Min | Hokkien POJ | Tâi-lô | ||||||
De vroegst bekende schriftelijke documentatie van het Chinese telraam dateert uit de 2e eeuw v. Chr.
Het Chinese telraam, bekend als suanpan (算盤/算盘, lit. “rekenblad”), is meestal 20 cm hoog en komt in verschillende breedtes, afhankelijk van de bediener. Het heeft gewoonlijk meer dan zeven staven. Er zijn twee kralen op elke staaf in het bovendek en vijf kralen in het onderdek. De kralen zijn meestal afgerond en van hardhout gemaakt. De kralen worden geteld door ze naar boven of naar beneden te bewegen in de richting van de balk; kralen die in de richting van de balk worden bewogen, worden geteld, die welke er vanaf worden bewogen niet. Een van de bovenste kralen is 5, terwijl een van de onderste kralen 1 is. Elke staaf heeft een cijfer eronder, dat de plaatswaarde aangeeft.De suanpan kan onmiddellijk in de beginpositie worden teruggezet door een snelle beweging langs de horizontale as om alle kralen weg te draaien van de horizontale balk in het midden.
Het prototype van het Chinese telraam verscheen tijdens de Han-dynastie, en de kralen zijn ovaal. De Song Dynastie en eerder gebruikten het 1:4 type of vierkralen telraam vergelijkbaar met het moderne telraam met inbegrip van de vorm van de kralen algemeen bekend als Japanse stijl telraam.
In de vroege Ming Dynastie, begon het telraam te verschijnen in de vorm van 1:5 telraam. Het bovenste dek had een kraal en de bodem had vijf kralen.
In de late Ming Dynastie, de abacus stijlen verscheen in de vorm van 2:5. Het bovenste dek had twee kralen en het onderste dek vijf kralen.
Verschillende rekentechnieken werden bedacht voor Suanpan om efficiënt te kunnen rekenen. Er zijn tegenwoordig scholen die studenten leren hoe ze het moeten gebruiken.
In de lange rol Langs de rivier tijdens het Qingming Festival geschilderd door Zhang Zeduan tijdens de Song dynastie (960-1297), is een suanpan duidelijk zichtbaar naast een boekhouding en doktersvoorschriften op de toonbank van een apotheek (Feibao).
De gelijkenis van het Romeinse telraam met het Chinese suanpan suggereert dat het ene het andere zou kunnen hebben geïnspireerd, aangezien er enig bewijs is van een handelsrelatie tussen het Romeinse Rijk en China. Een rechtstreeks verband kan echter niet worden aangetoond, en de gelijkenis van de telramen kan toeval zijn, beide uiteindelijk voortgekomen uit het tellen met vijf vingers per hand. Waar het Romeinse model (zoals de meeste moderne Koreaanse en Japanse) 4 plus 1 kraal per decimaal heeft, heeft de standaard suanpan 5 plus 2. Dit maakt overigens het gebruik mogelijk van een hexadecimaal getallensysteem (of een basis tot 18), dat wellicht werd gebruikt voor traditionele Chinese gewichtsmaten. (In plaats van op draden te lopen zoals bij de Chinese, Koreaanse en Japanse modellen, lopen de kralen van het Romeinse model in groeven, waardoor rekenkundige berekeningen vermoedelijk veel langzamer gaan.
Een andere mogelijke bron van de suanpan zijn Chinese telstaven, die met een decimaal stelsel werkten maar het begrip nul als plaatshouder misten. De nul werd waarschijnlijk in de Tang-dynastie (618-907) bij de Chinezen geïntroduceerd, toen reizen in de Indische Oceaan en het Midden-Oosten direct contact met India zouden hebben opgeleverd, waardoor zij het begrip nul en de decimale punt van Indische kooplieden en wiskundigen konden overnemen.
RomeinsEdit

De normale methode van rekenen in het oude Rome was, evenals in Griekenland, door het verplaatsen van tellers op een gladde tafel. Oorspronkelijk werden hiervoor kiezelstenen (calculi) gebruikt. Later, en in middeleeuws Europa, werden jetons vervaardigd. Gemarkeerde lijnen gaven eenheden, vijven, tienen enz. aan, zoals in het Romeinse getallenstelsel. Dit systeem van “tegengieten” werd voortgezet in het laat-Romeinse keizerrijk en in middeleeuws Europa, en bleef in beperkte mate in gebruik tot in de negentiende eeuw. Door de herinvoering van het telraam door paus Sylvester II, met wijzigingen, werd het in de elfde eeuw opnieuw algemeen gebruikt in Europa. Dit telraam gebruikte kralen aan draden, in tegenstelling tot de traditionele Romeinse telborden, waardoor het telraam veel sneller kon worden gebruikt.
Horatius schrijft in de 1e eeuw v. Chr. over het telraam van was, een plank bedekt met een dun laagje zwarte was waarop met een stylus zuilen en cijfers werden gegraveerd.
Een voorbeeld van archeologisch bewijs van het Romeinse telraam, hier in reconstructie weergegeven, dateert uit de 1e eeuw n. Chr. Het heeft acht lange groeven met elk tot vijf kralen en acht kortere groeven met elk één of geen kralen. De met I gemerkte groef geeft eenheden aan, X tientallen, en zo verder tot miljoenen. De kralen in de kortere groeven geven vijfenvijftig eenheden aan, vijf tientallen enz., in wezen in een binair gecodeerd decimaal stelsel, verwant aan de Romeinse cijfers. De korte groeven aan de rechterzijde kunnen zijn gebruikt voor het markeren van Romeinse “ounces” (d.w.z. fracties).
IndianEdit
De Abhidharmakośabhāṣya van Vasubandhu (316-396), een Sanskriet werk over boeddhistische filosofie, zegt dat de tweede-eeuwse filosoof Vasumitra zei dat “het plaatsen van een lont (Sanskriet vartikā) op het getal één (ekāṅka) betekent dat het een één is, terwijl het plaatsen van de lont op het getal honderd betekent dat het een honderd heet, en op het getal duizend betekent dat het een duizend is”. Het is onduidelijk wat deze opstelling precies geweest kan zijn. Rond de 5e eeuw vonden Indiase klerken al nieuwe manieren om de inhoud van de Abacus vast te leggen. Hindoeïstische teksten gebruikten de term śūnya (nul) om de lege kolom op het telraam aan te duiden.
JapansEdit

In het Japans wordt het telraam soroban (算盤, そろばん, lit. “Telblad”) genoemd, dat in de 14e eeuw uit China werd ingevoerd. Het werd waarschijnlijk al een eeuw of langer door de arbeidersklasse gebruikt voordat de heersende klasse ermee begon, omdat de klassenstructuur niet toeliet dat apparaten die door de lagere klasse werden gebruikt, door de heersende klasse werden overgenomen of gebruikt. Het 1/4 telraam, dat de zelden gebruikte tweede en vijfde kraal verwijdert, werd populair in de jaren 1940.
Het huidige Japanse telraam is van het 1:4 type, het telraam met vier kralens werd in de Muromachi-tijd uit China ingevoerd. Het heeft de vorm van het bovenste dek één kraal en de onderste vier kralen. De bovenste kraal op het bovendek is gelijk aan vijf en de onderste kraal is gelijk aan één zoals het Chinese of Koreaanse telraam, en het decimale getal kan worden uitgedrukt, zodat het telraam is ontworpen als een viertal telramen. De kralen hebben altijd de vorm van een ruit. In het algemeen wordt de quotiëntdeling gebruikt in plaats van de delingsmethode; om de vermenigvuldigings- en delingscijfers consequent te maken, wordt tegelijkertijd de delingsvermenigvuldiging gebruikt. Later had Japan een 3:5 abacus, genaamd 天三算盤, die nu de Ize Rongji collectie van Shansi Village in Yamagata City is. Er waren ook telramen van het 2:5 type.
Met de verspreiding van het telraam met vier kralen, is het ook gebruikelijk om het Japanse telraam over de hele wereld te gebruiken. Er zijn ook verbeterde Japanse telramen op verschillende plaatsen. Een van de in China gemaakte Japanse telramen is een plastic kralen telraam met een aluminium frame. Het bestand is naast de vier kralen, en de “clearing” knop, druk op de clearing-knop, onmiddellijk zet de bovenste kraal naar de bovenste positie, de onderste kraal wordt gekozen om de onderste positie, onmiddellijk clearing, makkelijk te gebruiken.
Het telraam wordt nog steeds vervaardigd in Japan vandaag, zelfs met de proliferatie, de bruikbaarheid en betaalbaarheid van zak elektronische rekenmachines. Het gebruik van de soroban wordt nog steeds onderwezen in Japanse lagere scholen als onderdeel van wiskunde, voornamelijk als een hulpmiddel om sneller mentaal te kunnen rekenen. Met behulp van visuele beelden van een soroban, kan men tot het antwoord komen in dezelfde tijd als, of zelfs sneller dan, mogelijk is met een fysiek instrument.
KoreanEdit
De Chinese abacus migreerde van China naar Korea rond 1400 AD. Koreanen noemen het jupan (주판), supan (수판) of jusan (주산).De vier kralen abacus( 1:4) werd geïntroduceerd in Korea Goryeo Dynastie uit de China tijdens Song Dynastie, later de vijf kralen abacus (5:1) abacus werd geïntroduceerd in het Koreaans uit China tijdens de Ming Dynastie.
Native AmericanEdit


Sommige bronnen vermelden het gebruik van een telraam, nepohualtzintzin genaamd, in de oude Azteekse cultuur. Dit Meso-Amerikaanse telraam gebruikte een 5-cijferig basis-20 systeem.Het woord Nepōhualtzintzin komt uit het Nahuatl en het wordt gevormd door de wortels; Ne – persoonlijk -; pōhual of pōhualli – de rekening -; en tzintzin – kleine gelijksoortige elementen. De volledige betekenis werd opgevat als: tellen met kleine gelijksoortige elementen door iemand. Het gebruik ervan werd in de Calmecac aangeleerd aan de temalpouhqueh , die studenten waren die waren opgedragen om de rekeningen van de hemelen op te nemen, van kindsbeen af.
De Nepōhualtzintzin was verdeeld in twee hoofddelen, gescheiden door een staaf of tussenkoord. In het linkerdeel bevonden zich vier kralen, die in de eerste rij eenheidswaarden hebben (1, 2, 3, en 4), en in het rechterdeel drie kralen met waarden van respectievelijk 5, 10, en 15. Om de waarde van de respectieve kralen van de bovenste rijen te kennen, volstaat het de waarde van de overeenkomstige rekening van de eerste rij met 20 te vermenigvuldigen (met elke rij).
In totaal waren er 13 rijen met 7 kralen in elke rij, die samen 91 kralen in elke Nepōhualtzintzin vormden. Dit was een fundamenteel getal om te begrijpen, 7 maal 13, een nauwe relatie bedacht tussen natuurverschijnselen, de onderwereld en de cycli van de hemelen. Eén Nepōhualtzintzin (91) vertegenwoordigde het aantal dagen dat een seizoen van het jaar duurt, twee Nepōhualtzitzin (182) is het aantal dagen van de cyclus van het graan, van het zaaien tot de oogst, drie Nepōhualtzintzin (273) is het aantal dagen van de dracht van een baby, en vier Nepōhualtzintzin (364) voltooide een cyclus en benaderde een jaar (11/4 dagen tekort). Vertaald in moderne computerrekenkunde kwam de Nepōhualtzintzin overeen met de rang van 10 tot de 18 in floating point, die zowel stellaire als infinitesimale hoeveelheden met absolute precisie berekende, wat betekende dat er geen afronding was toegestaan.
De herontdekking van de Nepōhualtzintzin was te danken aan de Mexicaanse ingenieur David Esparza Hidalgo, die op zijn zwerftochten door Mexico diverse gravures en schilderingen van dit instrument heeft gevonden en er verschillende van heeft gereconstrueerd, gemaakt van goud, jade, encrustaties van schelpen, enz. Er zijn ook zeer oude Nepōhualtzintzin gevonden die worden toegeschreven aan de Olmec-cultuur, en zelfs enkele armbanden van Maya-oorsprong, evenals een verscheidenheid aan vormen en materialen in andere culturen.
George I. Sanchez, “Arithmetic in Maya”, Austin-Texas, 1961 vond op het schiereiland Yucatán een ander telraam met basis 5 en basis 4, dat ook kalendergegevens berekende. Dit was een vingerabacus, waarbij aan de ene kant 0, 1, 2, 3, en 4 werden gebruikt; en aan de andere kant 0, 1, 2 en 3. Let op het gebruik van de nul aan het begin en einde van de twee cycli. Sanchez werkte samen met Sylvanus Morley, een bekend Mayanist.
De quipu van de Inca’s was een systeem van gekleurde geknoopte koorden die werden gebruikt om numerieke gegevens vast te leggen, zoals geavanceerde telstokken – maar niet werden gebruikt om berekeningen uit te voeren. Berekeningen werden uitgevoerd met een yupana (Quechua voor “telinstrument”; zie afbeelding) die na de verovering van Peru nog steeds in gebruik was. Het werkingsprincipe van een yupana is onbekend, maar in 2001 werd een verklaring van de wiskundige basis van deze instrumenten voorgesteld door de Italiaanse wiskundige Nicolino De Pasquale. Door de vorm van verschillende yupana’s te vergelijken, ontdekten onderzoekers dat berekeningen gebaseerd waren op de Fibonacci-reeks 1, 1, 2, 3, 5 en machten van 10, 20 en 40 als plaatswaarden voor de verschillende velden in het instrument. Door gebruik te maken van de Fibonacci-reeks kon het aantal korrels binnen een veld tot een minimum worden beperkt.
RussischEdit

Het Russische telraam, de schoty (Russisch: счёты, meervoud van Russisch: счёт, tellen), heeft gewoonlijk een enkel schuin dek, met tien kralen op elke draad (behalve één draad, meestal dicht bij de gebruiker, met vier kralen voor kwart-relevante breuken). Oudere modellen hebben nog een draad met 4 kralen voor kwart-kopeks, die tot 1916 werden geslagen. De Russische abacus wordt vaak verticaal gebruikt, met elke draad van links naar rechts als lijnen in een boek. De draden zijn gewoonlijk zo gebogen dat ze in het midden naar boven opbollen, zodat de kralen aan een van de twee zijden worden vastgepind. Het is vrijgemaakt wanneer alle kralen naar rechts zijn verplaatst. Bij manipulatie worden de kralen naar links bewogen. Om het zicht te vergemakkelijken, hebben de middelste 2 kralen op elke draad (de 5e en 6e kraal) gewoonlijk een andere kleur dan de andere acht kralen. Evenzo kan de linker kraal van de duizenddraad (en de miljoendraad, indien aanwezig) een andere kleur hebben.
Als eenvoudig, goedkoop en betrouwbaar apparaat was het Russische telraam in gebruik in alle winkels en op alle markten in de gehele voormalige Sovjet-Unie, en het gebruik ervan werd op de meeste scholen onderwezen tot in de jaren negentig. Zelfs de uitvinding van de mechanische rekenmachine van 1874, de Odhner rekenmachine, had ze in Rusland niet vervangen; volgens Jakov Perelman was het zelfs in zijn tijd bekend dat sommige zakenlieden die probeerden dergelijke toestellen in het Russische Rijk in te voeren, het opgaven en vertwijfeld vertrokken nadat ze het werk van een bekwame abacusbediener hadden gezien. Ook de massaproductie van Felix rekenmachines sinds 1924 heeft het gebruik ervan in de Sovjet-Unie niet noemenswaardig doen afnemen. Het Russische telraam begon pas aan populariteit in te boeten nadat de massaproductie van microcalculators in de Sovjet-Unie in 1974 op gang was gekomen. Tegenwoordig wordt het als een archaïsme beschouwd en vervangen door de handrekenmachine.
Het Russische telraam werd rond 1820 naar Frankrijk gebracht door de wiskundige Jean-Victor Poncelet, die in het leger van Napoleon diende en krijgsgevangene in Rusland was geweest. De abacus was in West-Europa in de 16e eeuw in onbruik geraakt door de opkomst van de decimale notatie en de algoritmische methoden. Voor Poncelet’s Franse tijdgenoten was het iets nieuws. Poncelet gebruikte het, niet voor een toegepast doel, maar als hulpmiddel bij onderwijs en demonstratie. De Turken en de Armeniërs gebruikten ook abacussen, vergelijkbaar met de Russische schoty. Het werd een coulba genoemd door de Turken en een choreb door de Armeniërs.