De standaardafwijking is de gemiddelde hoeveelheid variabiliteit in uw dataset. Het vertelt u, gemiddeld, hoe ver elke waarde van het gemiddelde afligt.
Een hoge standaardafwijking betekent dat waarden over het algemeen ver van het gemiddelde afliggen, terwijl een lage standaardafwijking aangeeft dat waarden dicht bij het gemiddelde liggen.
Wat vertelt de standaardafwijking u?
Standaardafwijking is een nuttige maat voor spreiding bij normale verdelingen.
In normale verdelingen zijn gegevens symmetrisch verdeeld zonder scheefheid. De meeste waarden groeperen zich rond een centraal gebied, met waarden die afnemen naarmate ze verder van het centrum verwijderd zijn. De standaardafwijking vertelt je hoe ver je gegevens gemiddeld van het centrum van de verdeling afliggen.
Veel wetenschappelijke variabelen volgen normale verdelingen, zoals lengte, gestandaardiseerde testscores of beoordelingen van werktevredenheid. Als je de standaardafwijkingen van verschillende steekproeven hebt, kun je hun verdelingen met statistische tests vergelijken om conclusies te trekken over de grotere populaties waaruit ze afkomstig zijn.
De gemiddelde (M) beoordelingen zijn hetzelfde voor elke groep – het is de waarde op de x-as wanneer de curve op zijn hoogtepunt is. Hun standaardafwijkingen (SD) verschillen echter van elkaar.
De standaardafwijking geeft de spreiding van de verdeling weer. De kromme met de laagste standaardafwijking heeft een hoge piek en een kleine spreiding, terwijl de kromme met de hoogste standaardafwijking meer vlak en verspreid is.
De empirische regel
De standaardafwijking en het gemiddelde samen kunnen u vertellen waar de meeste waarden in uw verdeling liggen als ze een normale verdeling volgen.
De empirische regel, of de 68-95-99.7 regel, vertelt u waar uw waarden liggen:
- Rond 68% van de scores ligt binnen 2 standaarddeviaties van het gemiddelde,
- Rond 95% van de scores ligt binnen 4 standaarddeviaties van het gemiddelde,
- Rond 99,7% van de scores ligt binnen 6 standaarddeviaties van het gemiddelde.7% van de scores ligt binnen 6 standaardafwijkingen van het gemiddelde.
Volgens de empirische regel:
- Rond 68% van de scores ligt tussen 40 en 60.
- Rond 95% van de scores ligt tussen 30 en 70.
- Rond 99,7% van de scores ligt tussen 20 en 80.
De empirische regel is een snelle manier om een overzicht van uw gegevens te krijgen en te controleren of er uitschieters of extreme waarden zijn die dit patroon niet volgen.
Voor niet-normale verdelingen is de standaardafwijking een minder betrouwbare maat voor de variabiliteit en moet deze worden gebruikt in combinatie met andere maatstaven, zoals het bereik of de interkwartielafstand.
Standaardafwijkingsformules voor populaties en steekproeven
Verschillende formules worden gebruikt voor het berekenen van standaardafwijkingen, afhankelijk van de vraag of u gegevens hebt van een hele populatie of van een steekproef.
Populatie-standaardafwijking
Wanneer u gegevens hebt verzameld van elk lid van de populatie waarin u bent geïnteresseerd, kunt u een exacte waarde krijgen voor de populatie-standaardafwijking.
De formule voor de standaardafwijking van de populatie ziet er als volgt uit:
| Formule | Uitleg |
|---|---|
 |
|
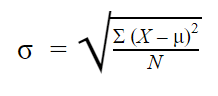Standaardafwijking van de steekproef
Wanneer u gegevens uit een steekproef verzamelt, wordt de standaardafwijking van de steekproef gebruikt om schattingen of gevolgtrekkingen te maken over de standaardafwijking van de populatie.
De formule voor de standaardafwijking van de steekproef ziet er als volgt uit:
| Formule | Uitleg |
|---|---|
 |
|
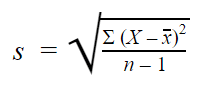Bij steekproeven gebruiken we n – 1 in de formule omdat het gebruik van n ons een vertekende schatting zou geven die de variabiliteit consequent onderschat. De standaardafwijking van de steekproef zou de neiging hebben lager te zijn dan de echte standaardafwijking van de populatie.
Vermindering van de steekproef n tot n – 1 maakt de standaardafwijking kunstmatig groot, waardoor u een conservatieve schatting van de variabiliteit krijgt.
Hoewel dit geen onvertekende schatting is, is het wel een minder vertekende schatting van de standaardafwijking: het is beter om de variabiliteit in steekproeven te overschatten dan te onderschatten.
Stappen voor het berekenen van de standaardafwijking
De standaardafwijking wordt meestal automatisch berekend door de software die u voor uw statistische analyse gebruikt. Maar u kunt het ook met de hand berekenen om beter te begrijpen hoe de formule werkt.
Er zijn zes hoofdstappen om de standaardafwijking met de hand te vinden. We zullen een kleine dataset van 6 scores gebruiken om de stappen te doorlopen.
| Gegevensverzameling | |||||
|---|---|---|---|---|---|
| 46 | 69 | 32 | 60 | 52 | 41 |
Stap 1: Vind het gemiddelde
Om het gemiddelde te vinden, telt u alle scores bij elkaar op en deelt u ze vervolgens door het aantal scores.
x̅ = (46 + 69 + 32 + 60 + 52 + 41) ÷ 6 = 50
Stap 2: Bepaal de afwijking van elke score van het gemiddelde
Trek het gemiddelde van elke score af om de afwijkingen van het gemiddelde te krijgen.
Sinds x̅ = 50, trekken we hier van elke score 50 af.
| Score | Afwijking van het gemiddelde |
|---|---|
| 46 | 46 – 50 = -4 |
| 69 | 69 – 50 = 19 |
| 32 | 32 – 50 = -18 |
| 60 | 60 – 50 = 10 |
| 52 | 52 – 50 = 2 |
| 41 | 41 – 50 = -9 |
Stap 3: Kwadrateer elke afwijking van het gemiddelde
Vermenigvuldig elke afwijking van het gemiddelde met zichzelf. Dit levert positieve getallen op.
(-4)2 = 4 × 4 = 16
192 = 19 × 19 = 361
(-18)2 = -18 × -18 = 324
(-18)2 = -18 × -18 = 324
18 × -18 = 324
102 = 10 × 10 = 100
22 = 2 × 2 = 4
(-9)2 = -9 × -9 = 81
Stap 4: Vind de som van de kwadraten
Tel alle gekwadrateerde afwijkingen bij elkaar op. Dit wordt de som van de kwadraten genoemd.
16 + 361 + 324 + 100 + 4 + 81 = 886
Stap 5: Vind de variantie
Deel de som van de kwadraten door n – 1 (bij een steekproef) of N (bij een populatie) – dit is de variantie.
Omdat we met een steekproefgrootte van 6 werken, gebruiken we n – 1, waarbij n = 6.
886 ÷ (6 – 1) = 886 ÷ 5 = 177.2
Stap 6: Zoek de vierkantswortel van de variantie
Om de standaardafwijking te vinden, nemen we de vierkantswortel van de variantie.
√177,2 = 13,31
Uit het feit dat SD = 13.31, kunnen we zeggen dat elke score gemiddeld 13,31 punten van het gemiddelde afwijkt.
Waarom is standaarddeviatie een nuttige maat voor variabiliteit?
Hoewel er eenvoudiger manieren zijn om variabiliteit te berekenen, weegt de standaarddeviatieformule ongelijkmatig gespreide steekproeven zwaarder dan gelijkmatig gespreide steekproeven. Een hogere standaardafwijking vertelt u dat de verdeling niet alleen meer verspreid is, maar ook ongelijkmatiger.
Dit betekent dat het u een beter idee geeft van de variabiliteit van uw gegevens dan eenvoudigere maatstaven, zoals de gemiddelde absolute afwijking (MAD).
De MAD is vergelijkbaar met de standaardafwijking, maar eenvoudiger te berekenen. Eerst drukt u elke afwijking van het gemiddelde uit in absolute waarden door ze om te zetten in positieve getallen (bijvoorbeeld, -3 wordt 3). Vervolgens bereken je het gemiddelde van deze absolute afwijkingen.
In tegenstelling tot de standaardafwijking hoef je voor de MAD geen kwadraten of wortels van getallen te berekenen. Maar om die reden geeft het een minder nauwkeurige maat voor de variabiliteit.
Nemen we twee steekproeven met dezelfde centrale tendens maar verschillende hoeveelheden variabiliteit. Monster B is variabeler dan monster A.
| Values | Mean | Mean absolute deviatie | Standard deviatie | |
|---|---|---|---|---|
| Sample A | 66, 30, 40, 64 | 50 | 15 | 17.8 |
| Sample B | 51, 21, 79, 49 | 50 | 15 | 23.7 |
Voor steekproeven met gelijke gemiddelde afwijkingen van het gemiddelde kan de MAD geen onderscheid maken tussen de niveaus van spreiding. De standaardafwijking is nauwkeuriger: deze is hoger voor de steekproef met meer variabiliteit in afwijkingen van het gemiddelde.
Door de verschillen ten opzichte van het gemiddelde te kwadrateren, geeft de standaardafwijking de ongelijke spreiding nauwkeuriger weer. Deze stap weegt extreme afwijkingen zwaarder dan kleine afwijkingen.
Dit maakt de standaarddeviatie echter ook gevoelig voor uitschieters.
Veel gestelde vragen over standaarddeviatie
Variabiliteit wordt meestal gemeten met de volgende beschrijvende statistieken:
- Bereik: het verschil tussen de hoogste en de laagste waarde
- Interkwartielbereik: het bereik van de middelste helft van een verdeling
- Standaardafwijking: gemiddelde afstand tot het gemiddelde
- Variantie: gemiddelde van gekwadrateerde afstanden tot het gemiddelde
De standaardafwijking is de gemiddelde mate van variabiliteit in uw gegevensverzameling. Het vertelt je, gemiddeld, hoe ver elke score van het gemiddelde afligt.
In normale verdelingen betekent een hoge standaardafwijking dat waarden over het algemeen ver van het gemiddelde afliggen, terwijl een lage standaardafwijking aangeeft dat waarden dicht bij het gemiddelde zijn geclusterd.
Bij een normale verdeling zijn de gegevens symmetrisch verdeeld, zonder scheefheid. De meeste waarden groeperen zich rond een centraal gebied, waarbij de waarden afnemen naarmate ze verder van het centrum af liggen.
De maten van centrale tendens (gemiddelde, modus en mediaan) zijn bij een normale verdeling precies gelijk.
De empirische regel, of de 68-95-99.7-regel, vertelt u waar de meeste waarden in een normale verdeling liggen:
- Rond 68% van de waarden ligt binnen 1 standaardafwijking van het gemiddelde.
- Rond 95% van de waarden ligt binnen 2 standaardafwijkingen van het gemiddelde.
- Rond 99,7% van de waarden ligt binnen 3 standaardafwijkingen van het gemiddelde.
- Rond 99,7% van de waarden ligt binnen 3 standaardafwijkingen van het gemiddelde.
De empirische regel is een snelle manier om een overzicht van uw gegevens te krijgen en te controleren of er uitschieters of extreme waarden zijn die dit patroon niet volgen.
Variantie is het gemiddelde van de gekwadrateerde afwijkingen van het gemiddelde, terwijl standaarddeviatie de vierkantswortel van dit getal is. Beide maten geven de variabiliteit in een verdeling weer, maar hun eenheden verschillen:
- Standaardafwijking wordt uitgedrukt in dezelfde eenheden als de oorspronkelijke waarden (bijv. minuten of meters).
- Variantie wordt uitgedrukt in veel grotere eenheden (bijv. meters in het kwadraat).
Hoewel de eenheden van variantie moeilijker intuïtief te begrijpen zijn, is variantie belangrijk in statistische tests.