Principes van Satellietcommunicatie

Een satelliet is een lichaam dat rond een ander lichaam beweegt in een mathematisch voorspelbaar pad dat een baan wordt genoemd. Een communicatiesatelliet is niets anders dan een microgolf-repeaterstation in de ruimte dat nuttig is voor telecommunicatie, radio en televisie, samen met internettoepassingen.

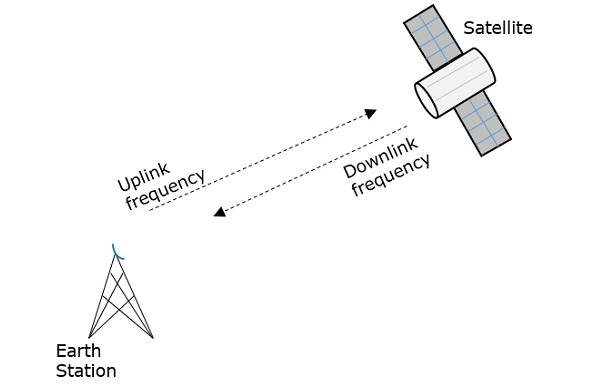
Een repeater is een schakeling die de sterkte van het ontvangen signaal verhoogt en het opnieuw uitzendt. Maar hier werkt deze repeater als een transponder, die de frequentieband van het uitgezonden signaal verandert van het ontvangen signaal.

De frequentie waarmee het signaal de ruimte in wordt gezonden wordt Uplink-frequentie genoemd, terwijl de frequentie waarmee het door de transponder wordt gezonden Downlink-frequentie is.

De volgende figuur illustreert dit concept duidelijk.

Nu, laten we eens kijken naar de voordelen, nadelen en toepassingen van satellietcommunicatie.

Satellietcommunicatie – Voordelen

Er zijn vele voordelen van satellietcommunicatie, zoals –

• Flexibiliteit

• Gemak bij het installeren van nieuwe circuits

• Gemakkelijke afstanden en de kosten doen er niet toe

• Broadcasting mogelijkheden

• Elke uithoek van de aarde wordt gedekt

• De gebruiker kan het netwerk beheren

Satellietcommunicatie – Nadelen

Satellietcommunicatie heeft de volgende nadelen –

• De initiële kosten zoals segment- en lanceerkosten zijn te hoog.

• Congestie van frequenties

• Interferentie en propagatie

Satellietcommunicatie – Toepassingen

Satellietcommunicatie vindt zijn toepassingen op de volgende gebieden –

• In radio-uitzendingen.

• In televisie-uitzendingen zoals DTH.

• In internettoepassingen zoals het verschaffen van een internetverbinding voor gegevensoverdracht, GPS-toepassingen, surfen op internet, enz.

• voor spraakcommunicatie.

• voor onderzoek en ontwikkeling, op vele gebieden.

• in militaire toepassingen en navigaties.

De oriëntatie van de satelliet in zijn baan hangt af van de drie wetten die de wetten van Kepler worden genoemd.

De Wetten van Kepler

Johannes Kepler (1571-1630), de astronomische wetenschapper, gaf 3 revolutionaire wetten, betreffende de beweging van satellieten. Het pad dat door een satelliet rond zijn primaire (de aarde) wordt gevolgd, is een ellips. De ellips heeft twee brandpunten – F1 en F2, waarvan de aarde er een is.

Als men de afstand van het middelpunt van het hemellichaam tot een punt op zijn elliptische baan beschouwt, dan heet het verste punt van een ellips vanaf het middelpunt apogeum en het kortste punt van een ellips vanaf het middelpunt heet perigeum.

De 1e Wet van Kepler

De 1e Wet van Kepler stelt dat, “elke planeet in een elliptische baan om de zon draait, met de zon als een van zijn brandpunten.” Zo beweegt een satelliet in een elliptische baan met de aarde als een van haar brandpunten.

De halve hoofdas van de ellips wordt aangeduid als ‘a’ en de halve korte as wordt aangeduid als b. Daarom kan de excentriciteit e van dit stelsel geschreven worden als –

$$e = \frac{\sqrt{a^{2}-b^{2}}{a}$$

• Eccentriciteit (e) – Het is de parameter die het verschil bepaalt in de vorm van de ellips ten opzichte van die van een cirkel.

• Semi-grote as (a) – Dit is de langste diameter die de twee brandpunten langs het middelpunt verbindt en die beide apogees (de verste punten van een ellips vanaf het middelpunt) raakt.

• Semi-kleine as (b) – Het is de kortste diameter getrokken door het middelpunt, die beide perigees (kortste punten van een ellips vanuit het middelpunt) raakt.

Deze zijn goed beschreven in de volgende figuur.

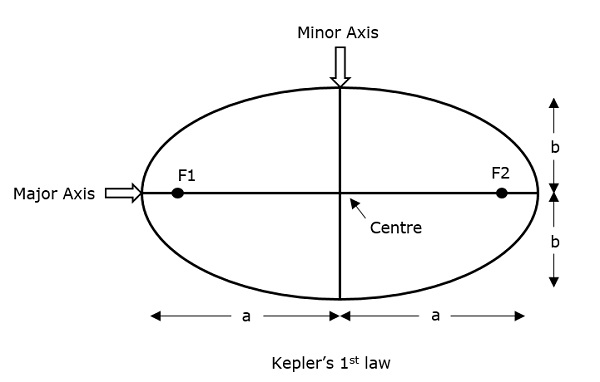
Voor een elliptische baan is het altijd wenselijk dat de excentriciteit tussen 0 en 1 ligt, d. w. z.d.w.z. 0 < e < 1 want als e nul wordt, zal het pad geen elliptische vorm meer hebben maar zal het worden omgezet in een cirkelvormig pad.

De 2e wet van Kepler

De 2e wet van Kepler stelt dat, “Voor gelijke tijdsintervallen is de oppervlakte die door de satelliet wordt bestreken gelijk ten opzichte van het middelpunt van de aarde.”

Dit kan begrepen worden door de volgende figuur te bekijken.

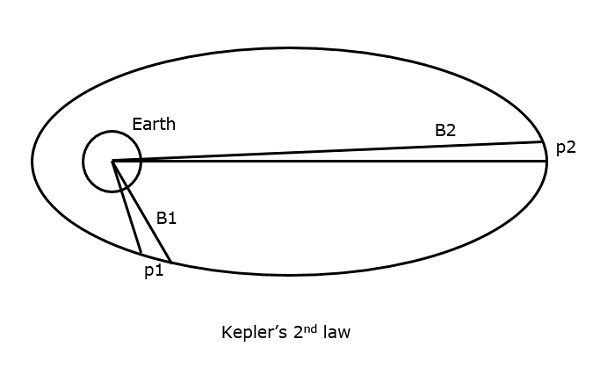
Stel dat de satelliet p1 en p2 afstanden aflegt, in hetzelfde tijdsinterval, dan zijn de oppervlakten B1 en B2 die in beide gevallen respectievelijk worden bestreken, gelijk.

De 3e wet van Kepler

De 3e wet van Kepler stelt dat: “Het kwadraat van de periodieke tijd van de baan evenredig is met de kubus van de gemiddelde afstand tussen de twee hemellichamen.”

Dit kan wiskundig geschreven worden als

$$T^{2}:^{3}:^:a^{3}$

Wat impliceert

$$T^{2} = \frac{4\pi ^{2}}{GM}a^{3}$$

Waarbij $\frac{4\pi ^{2}}{GM}$ de evenredigheidsconstante is (volgens de Newtoniaanse Mechanica)

$$T^{2} = \frac{4\pi ^{2}}{\mu}a^{3} $$

Waar μ = de geocentrische gravitatieconstante van de aarde, i.d.w.z. μ = 3.986005 × 1014 m3/sec2

$$1 = ^{2}\frac{2\pi}{T} \right )^{2}\frac{a^{3}}{\mu}$$

$1 = n^{2}\frac{a^{3}}{\mu}:\:\:\:\:a^{3} = \frac{\mu}{n^{2}}$$

Waarbij n = de gemiddelde beweging van de satelliet in radialen per seconde

De baanwerking van satellieten wordt berekend met behulp van deze wetten van Kepler.

Daarnaast is er nog een belangrijk ding dat moet worden opgemerkt. Een satelliet, wanneer hij rond de aarde draait, ondergaat een trekkracht van de aarde die de gravitatiekracht is. Ook ondervindt hij enige trekkracht van de zon en de maan. Er werken dus twee krachten op hem in. Deze zijn –

• Centripetale kracht – De kracht die de neiging heeft een voorwerp dat zich in een baan voortbeweegt naar zich toe te trekken, wordt centripetale kracht genoemd.

• Centrifugale kracht – De kracht die de neiging heeft een voorwerp dat zich in een baan voortbeweegt van zijn plaats weg te duwen, wordt centrifugale kracht genoemd.

Een satelliet moet deze twee krachten dus in evenwicht houden om zichzelf in zijn baan te houden.

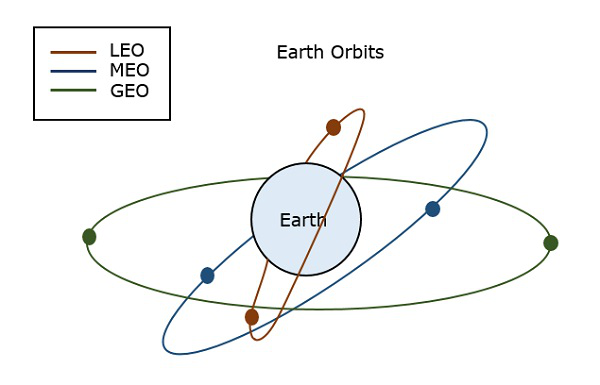
Aardebanen

Een satelliet die in de ruimte wordt gelanceerd, moet in een bepaalde baan worden geplaatst om zijn omwenteling op een bepaalde manier mogelijk te maken, zodat hij bereikbaar blijft en zijn doel kan dienen, of dat nu wetenschappelijk, militair of commercieel is. Dergelijke banen die aan satellieten worden toegewezen ten opzichte van de aarde worden aardbanen genoemd. De satellieten in deze banen zijn Aarde Baan Satellieten.

De belangrijke soorten aardbanen zijn –

• Geo-synchrone aardbaan

• Medium aardbaan

• Lage aardbaan

Geosynchrone aardbaansatellieten

Een Geo-Synchrone Aardbaan (GEO) satelliet is er een die op een hoogte van 22,300 mijl boven de aarde. Deze baan is gesynchroniseerd met een zijde echte dag (d.w.z., 23 uur 56 minuten). Deze baan kan inclinatie en eccentriciteit hebben. Hij mag niet cirkelvormig zijn. Deze baan kan gekanteld zijn aan de polen van de aarde. Maar hij lijkt stationair wanneer hij vanaf de aarde wordt waargenomen.

Dezelfde geo-synchrone baan, als hij cirkelvormig is en in het vlak van de evenaar, wordt hij geostationaire baan genoemd. Deze satellieten zijn geplaatst op 35.900 km (hetzelfde als geosynchrone) boven de evenaar van de aarde en zij blijven draaien ten opzichte van de richting van de aarde (van west naar oost). Deze satellieten worden beschouwd als stationair ten opzichte van de aarde en vandaar de naam.

Geostationaire aardbaan satellieten worden gebruikt voor weersvoorspelling, satelliet-tv, satellietradio en andere vormen van wereldwijde communicatie.

De volgende figuur toont het verschil tussen geo-synchrone en geostationaire banen. De rotatie-as geeft de beweging van de aarde aan.

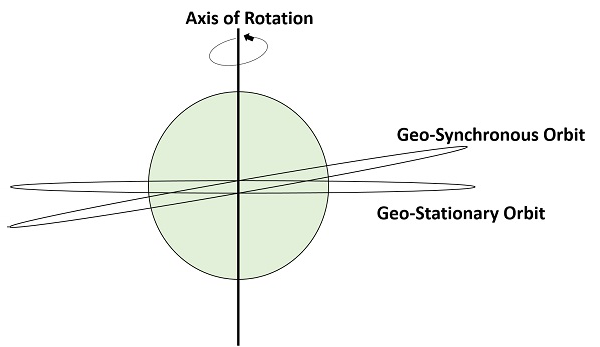
Note – Elke geostationaire baan is een geo-synchrone baan. Maar elke geo-synchrone baan is GEEN geostationaire baan.

Medium Earth Orbit Satellites

Medium Earth Orbit (MEO)-satellietnetwerken draaien op afstanden van ongeveer 8000 mijl van het aardoppervlak. Signalen die door een MEO-satelliet worden uitgezonden, leggen een kortere afstand af. Dit vertaalt zich in een betere signaalsterkte aan de ontvangstzijde. Dit betekent dat aan de ontvangstzijde kleinere, lichtere ontvangstterminals kunnen worden gebruikt.

Omdat het signaal een kortere afstand van en naar de satelliet aflegt, is er minder transmissievertraging. De transmissievertraging kan worden gedefinieerd als de tijd die een signaal nodig heeft om naar een satelliet te reizen en weer terug naar een ontvangststation.

Voor real time-communicatie geldt dat hoe korter de transmissievertraging is, des te beter het communicatiesysteem zal zijn. Als een GEO-satelliet bijvoorbeeld 0,25 seconden nodig heeft voor een rondreis, dan heeft een MEO-satelliet minder dan 0,1 seconden nodig om dezelfde reis te voltooien. MEO’s werken in het frequentiegebied van 2 GHz en hoger.

Low Earth Orbit Satellites

De Low Earth Orbit (LEO) satellieten worden hoofdzakelijk ingedeeld in drie categorieën, namelijk kleine LEO’s, grote LEO’s, en Mega-LEO’s. LEO’s draaien in een baan op een afstand van 500 tot 1000 mijl boven het aardoppervlak.

Door deze betrekkelijk korte afstand wordt de transmissievertraging beperkt tot slechts 0,05 seconden. Dit vermindert verder de behoefte aan gevoelige en omvangrijke ontvangstapparatuur. Kleine LEO’s zullen werken in het 800 MHz-bereik (0,8 GHz). Big LEO’s zullen opereren in het 2 GHz-bereik of hoger, en Mega-LEO’s opereren in het 20-30 GHz-bereik.

De hogere frequenties in verband met Mega-LEO’s vertalen zich in meer informatiedragende capaciteit en leveren de mogelijkheid van real-time, lage vertraging video-transmissieschema.

De volgende figuur toont de paden van LEO, MEO, en GEO.