
Probeer deze eerst eens op te lossen en uit te leggen zonder het antwoord te zien.
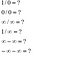
Deze termen proberen ons vaak in verwarring te brengen omdat de meesten van ons er niet het juiste begrip van hebben. Bekijk nu de antwoorden.

iets/0:
Je vraagt je misschien af na het zien van deze antwoorden. Als u dat niet bent, is het goed. Iets gedeeld door 0 is altijd ongedefinieerd omdat de waarde nog niet gedefinieerd is. Dus, wanneer zeggen we dat iets gedeeld door 0 oneindig is? We hebben dit natuurlijk al vaak gezien, maar waarom zeggen we dit?
Wel, iets gedeeld door 0 is oneindig is het enige geval waarin we limiet gebruiken. Oneindig is geen getal, het is de lengte van een getal. Wanneer we limiet gebruiken, denken we altijd dat x ergens naar toe neigt, niet dat x ergens gelijk aan is. Daarom kunnen we het getal niet raden. Omdat we het exacte getal niet kunnen raden, beschouwen we het als een lengte van een getal of oneindig. In normale gevallen is de waarde van iets gedeeld door 0 nog niet vastgesteld, dus is het onbepaald.
Indeterminate vorm:
0/0 en oneindig gedeeld door oneindig is onbepaald. Waarom? In dit geval zijn de wiskundige uitdrukkingen correct. Er zou een waarde moeten zijn, maar we hebben de exacte waarde nog niet bepaald. Soms kan het de waarde hebben of het kan onbepaald zijn. We weten het niet. Daarom zeggen we dat deze termen een onbepaalde vorm hebben.
Om diezelfde reden hebben oneindig min oneindig en (min oneindig min oneindig) beide een onbepaalde vorm, niet nul of min oneindig omdat oneindig elk positief of negatief getal kan zijn. Dus, min oneindig min oneindig zal niet altijd naar de negatieve richting gaan.
Een andere soortgelijke uitdrukking die oneindig vermenigvuldigd met 0 is, volgt deze regel. Daarom is het ook in de onbepaalde vorm.
1 gedeeld door oneindig:
In dit geval, als we een klein getal delen door een groot getal, komt het resultaat heel dicht bij nul te liggen. Daarom beschouwen we het als nul.
Voorbeeld: