
De beleidsvraag: Belastingvermindering voor de aankoop van hybride auto’s – Is dit de beste keuze van de overheid om het brandstofverbruik en de CO2-uitstoot te verminderen?
Inwoners van de VS en de overheid maken zich zorgen over de afhankelijkheid van geïmporteerde buitenlandse olie en de uitstoot van koolstof in de atmosfeer. In 2005 nam het Congres een wet aan om consumenten belastingvoordelen te geven voor de aankoop van elektrische en hybride auto’s.
Dit belastingvoordeel lijkt misschien een goede beleidskeuze, maar het is duur omdat het de inkomsten van de Amerikaanse regering rechtstreeks verlaagt. Zijn er effectievere benaderingen om de afhankelijkheid van fossiele brandstoffen en de uitstoot van koolstof te verminderen? Hoe beslissen we welk beleid het beste is? Om deze vraag te beantwoorden, moeten beleidsmakers met enige nauwkeurigheid voorspellen hoe consumenten op dit belastingbeleid zullen reageren voordat deze beleidsmakers miljoenen federale dollars uitgeven.
We kunnen het concept van nut toepassen op deze beleidsvraag. In deze module zullen we nut en nutsfuncties bestuderen. We zullen dan in staat zijn om een geschikte nutsfunctie te gebruiken om onverschilligheidscurven af te leiden die onze beleidsvraag beschrijven.
Beleidsvraag onderzoeken
Stel dat het belastingkrediet om de aankoop van hybride auto’s te subsidiëren een groot succes is en het gemiddelde brandstofverbruik van alle auto’s op de Amerikaanse wegen verdubbelt – een resultaat dat duidelijk niet realistisch is, maar nuttig is voor onze verdere discussies. Wat zou er volgens u gebeuren met het brandstofverbruik van alle automobilisten in de VS? Moet de regering verwachten dat het brandstofverbruik en de CO2-uitstoot van auto’s met de helft afnemen? Waarom wel of waarom niet?
2.1 nutsfuncties
LO 2.1: Beschrijf een nutsfunctie.
2.2 nutsfuncties en typische voorkeuren
LO 2.2: Identificeer nutsfuncties op basis van de typische voorkeuren die ze vertegenwoordigen.
2.3 Utility Functions and Indifference Curve Maps
LO 2.3: Leg uit hoe je een indifference curve uit een nutsfunctie afleidt.
2.4 Finding Marginal Utility and Marginal Rate of Substitution
LO 2.4: Leid het marginale nut en de MRS af voor typische nutsfuncties.
2.5. Beleidsvraag
2.1 nutsfuncties
LO1: Beschrijf een nutsfunctie.
Onze voorkeuren stellen ons in staat vergelijkingen te maken tussen verschillende consumptiebundels en de voorkeursbundels te kiezen. We kunnen bijvoorbeeld de rangorde van een hele reeks bundels bepalen op basis van onze voorkeuren. Een nutsfunctie is een wiskundige functie die bundels consumptiegoederen rangschikt door aan elk ervan een getal toe te kennen, waarbij grotere getallen wijzen op voorkeursbundels. nutsfuncties hebben de eigenschappen die we in module 1 met betrekking tot voorkeuren hebben vastgesteld. Dat wil zeggen: zij kunnen bundels ordenen, zij zijn volledig en transitief, meer heeft de voorkeur boven minder en, in relevante gevallen, zijn gemengde bundels beter.
Het getal dat de nutsfunctie aan een specifieke bundel toekent, staat bekend als het nutsgetal, de voldoening die een consument uit een specifieke bundel haalt. Het nutsgetal voor elke bundel betekent niets in absolute termen; er is geen uniforme schaal waaraan we de tevredenheid afmeten. Het enige nut is relatief: we kunnen het nut gebruiken om te bepalen welke bundels de voorkeur hebben boven andere.
Als het nut van bundel A hoger is dan het nut van bundel B, dan is dat gelijk aan te zeggen dat een consument de voorkeur geeft aan bundel A boven bundel B. Nutsfuncties rangschikken de voorkeuren van consumenten dus door aan elke bundel een getal toe te kennen. . We kunnen een nutsfunctie gebruiken om de in module 1 beschreven kaarten van de indifferentiecurve te tekenen. Aangezien alle bundels op dezelfde indifferentiekromme evenveel voldoening geven, en dus geen enkele de voorkeur geniet, heeft elke bundel hetzelfde nut. We kunnen dus een indifferentiekromme tekenen door alle bundels te bepalen die hetzelfde getal uit de nutsfunctie opleveren.
Economen zeggen dat nutsfuncties ordinaal zijn in plaats van kardinaal. Ordinaal betekent dat nutsfuncties alleen bundels rangschikken – ze geven alleen aan welke bundel beter is, niet hoeveel beter die is dan een andere bundel. Stel, bijvoorbeeld, dat een nutsfunctie aangeeft dat bundel A 10 nuts oplevert en bundel B 20 nuts. We zeggen niet dat bundel B twee keer zo goed is, of 10 keer beter, alleen dat de consument de voorkeur geeft aan bundel B. Stel bijvoorbeeld dat een vriendin meedeed aan een wedstrijd en u vertelde dat ze derde was geworden. Deze informatie is ordinaal: U weet dat ze sneller was dan de vierde en langzamer dan de tweede. Je weet alleen in welke volgorde de lopers zijn geëindigd. De individuele tijden zijn kardinaal: Als de eerste loper de race in precies één uur uitloopt en je vriendin in één uur en zes minuten, weet je dat je vriendin precies 10% langzamer was dan de snelste loper. Dit is waar zolang de ordening behouden blijft.
Neem bijvoorbeeld de nutsfunctie U die de voorkeuren beschrijft voor goederenbundels A en B: U(A,B). We kunnen elke positieve monotone transformatie op deze functie toepassen (wat in wezen betekent dat we de ordening niet veranderen) en de nieuwe functie die we hebben gecreëerd zal dezelfde voorkeuren weergeven. We kunnen bijvoorbeeld een positieve constante, α , vermenigvuldigen of een positieve of een negatieve constante, β , toevoegen. Dus αU(A,B)+β vertegenwoordigt precies dezelfde voorkeuren als U(A,B) omdat het de bundels op precies dezelfde manier zal ordenen. Dit feit is heel nuttig omdat soms de toepassing van een positief monotone transformatie van een nutsfunctie het oplossen van problemen vergemakkelijkt.
2.2 nutsfuncties en typische voorkeuren
LO2: Identificeer nutsfuncties op basis van de typische voorkeuren die ze vertegenwoordigen
Bedenk bundels appels, A, en bananen, B. Een nutsfunctie die de voorkeuren van Isaac voor bundels appels en bananen beschrijft, is de functie U(A,B). Maar wat zijn de specifieke voorkeuren van Isaac voor bundels appels en bananen? Stel dat Isaac tamelijk standaard voorkeuren heeft voor appels en bananen die leiden tot onze typische onverschilligheidskrommen: Hij heeft liever meer dan minder, en hij houdt van afwisseling. Een nutsfunctie die deze voorkeuren weergeeft, zou kunnen zijn:
U(A,B) = AB
Als appels en bananen elkaar perfect aanvullen in Isaacs voorkeuren, zou de nutsfunctie er ongeveer zo uitzien:
U(A,B) = MIN,
waarbij de MIN-functie eenvoudigweg de kleinste van de twee getallen als waarde van de functie toekent.
Als appels en bananen perfecte vervangingsproducten zijn, is de nutsfunctie additief en zou er ongeveer zo uitzien:
U(A,B) = A + B
Een klasse nutsfuncties die bekend staat als Cobb-Douglas nutsfuncties worden in de economie zeer vaak gebruikt, en wel om twee redenen:
1. Zij geven “goed gedragen” voorkeuren weer, zoals meer is beter en voorkeur voor variatie.
2. Zij zijn zeer flexibel en kunnen zeer gemakkelijk worden aangepast aan gegevens uit de echte wereld.
Cobb-Douglas nutsfuncties hebben deze vorm:
U(A,B) = AαBβ
Omdat positieve monotone transformaties dezelfde voorkeuren vertegenwoordigen, kan één zo’n transformatie worden gebruikt om α + β = 1 te stellen, wat we later zullen zien als een handige voorwaarde die sommige wiskunde in het consumentenkeuzeprobleem vereenvoudigt.
Een andere manier om de nutsfunctie op een nuttige manier te transformeren is de natuurlijke log van de functie te nemen, waardoor een nieuwe functie ontstaat die er als volgt uitziet:
U(A,B) = αln(A) + βln(B)
Om deze vergelijking af te leiden, past men eenvoudigweg de regels voor natuurlijke logs toe. . Het is belangrijk om het abstractieniveau hier in gedachten te houden. We kunnen gewoonlijk geen specifieke nutsfuncties maken die de individuele voorkeuren precies beschrijven. Waarschijnlijk zou niemand van ons zijn eigen voorkeuren kunnen beschrijven met een enkele vergelijking. Maar zolang consumenten in het algemeen voorkeuren hebben die overeenkomen met onze basisaannames, kunnen wij vrij goed nutsfuncties vinden die overeenkomen met consumptiegegevens uit de werkelijkheid. Later in de cursus zullen we hiervan het bewijs zien.
Tabel 2.1 geeft een overzicht van de voorkeuren en nutsfuncties die in dit hoofdstuk zijn beschreven.
|
Tabel 2.1 Soorten voorkeuren en de nutsfuncties die deze vertegenwoordigen |
||
|
PREFERENCES |
UTILITEIT FUNCTIE |
TYPE VAN UTILITEITSFUNCTIE |
|
Liefde voor afwisseling of “Goed Gedragen” |
U(A,B) = AB |
Cobb-Douglas |
|
Liefde voor Verscheidenheid of “Goed Gedragen” |
U(A,B) = AαBβ |
Cobb-Douglas |
|
Liefde voor Verscheidenheid of “Goed Gedragen” |
U(A,B) = αln(A) + βln(B) |
Natuurlijk Logboek Cobb-Douglas |
|
Perfecte Aanvullingen |
U(A,B) = MIN |
Min Functie |
|
Perfecte Substituten |
U(A,B) = A + B |
Additief |
2.3 Relateren van nutsfuncties en kaarten met indifferentiekrommen
LO3: Leg uit hoe uit een nutsfunctie een indifferentiekromme kan worden afgeleid
Indifference curves en nutsfuncties zijn direct aan elkaar verwant. In feite, aangezien indifferentiekrommen voorkeuren grafisch voorstellen en nutsfuncties voorkeuren mathematisch voorstellen, volgt hieruit dat indifferentiekrommen uit nutsfuncties kunnen worden afgeleid.
In univariate functies wordt de afhankelijke variabele op de verticale as en de onafhankelijke variabele op de horizontale as uitgezet, zoals de grafiek van y=f(x). Daarentegen zijn grafieken van bi-variate functies driedimensionaal, zoals U=U(A,B). Figuur 2.1 toont een grafiek van U=A^^frac{1}{2}B^^frac{1}{2}. Driedimensionale grafieken zijn nuttig om te begrijpen hoe het nut toeneemt naarmate de consumptie van zowel A als B toeneemt.
Figuur 2.1 U=A^frac{1}{2}B^frac{1}{2}
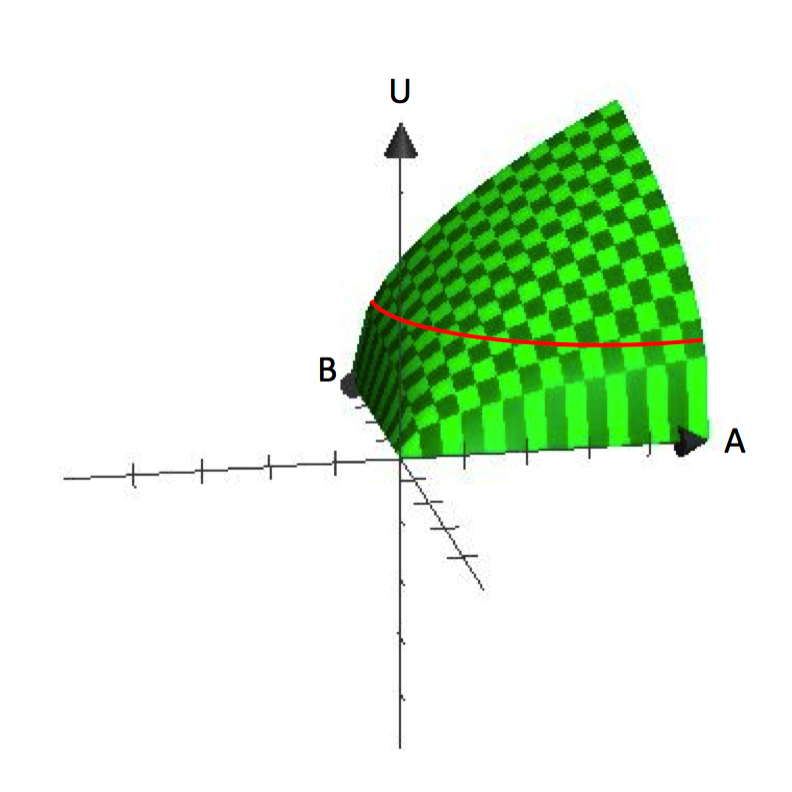
Figuur 2.1 laat duidelijk de veronderstelling zien dat consumenten een voorkeur hebben voor variëteit. Elke bundel die een bepaalde hoeveelheid van A en B bevat, vertegenwoordigt een punt op het oppervlak. De verticale hoogte van het oppervlak vertegenwoordigt het niveau van het nut. Door zowel A als B te verhogen, kan een consument hogere punten op het oppervlak bereiken.
Dus waar komen de indifferentiekrommen vandaan? Bedenk dat een indifferentiecurve een verzameling is van alle bundels die een consument onverschillig laat ten aanzien van de vraag welke bundel hij moet consumeren. Wiskundig komt dit erop neer dat alle bundels, wanneer ze in de nutsfunctie worden gezet, dezelfde functionele waarde opleveren. Dus als we een waarde voor het nut vaststellen, Ū, en alle bundels A en B vinden die die waarde genereren, dan definiëren we een onverschilligheidskromme. Merk op dat dit gelijk staat aan het vinden van alle bundels die de consument op dezelfde hoogte brengen op het driedimensionale oppervlak in figuur 2.1.
Indifferentiekrommen zijn een weergave van de hoogte (het nutspeil) op een plat oppervlak. In die zin zijn ze analoog aan een hoogtelijn op een topografische kaart. Door de driedimensionale grafiek terug te brengen naar de tweedimensionale ruimte – de A, B ruimte – kunnen we de hoogtelijnen/onverschilligheidscurven laten zien die verschillende hoogten of gebruiksniveaus vertegenwoordigen. Uit de grafiek in figuur 2.1 kunt u al aflezen hoe deze nutsfunctie indifferentiekrommen oplevert die “ingesnoerd” zijn of concaaf naar de oorsprong.
Dus indifferentiekrommen volgen rechtstreeks uit nutsfuncties en zijn een nuttige manier om nutsfuncties in een tweedimensionale grafiek weer te geven.
2.4 Het bepalen van het marginale nut en de marginale substitutievoet
LO4: Leid het marginale nut en de marginale substitutievoet af voor typische nutsfuncties.
Het marginale nut is het extra nut dat een consument ontvangt door één extra eenheid van een goed te consumeren. Dus
MU_{a}=(A+Delta A,B)-U(A,B)}{Delta A}
MU_{a}=(A+Delta A,B)-U(A,B)}{Delta A}
Merk op dat wanneer we het marginale nut van de consumptie van A onderzoeken, we B constant houden.
Rekenkundig gezien is het marginale nut hetzelfde als de partiële afgeleide van de nutsfunctie met betrekking tot A:
MU_{A}{\frac{Delta U(A,B)}{Delta A}
Neem een consument in gedachten die een maaltijd van salade en pizza gaat eten. Stel dat we de hoeveelheid salade constant houden – één salade bij een diner, bijvoorbeeld. Laten we nu het aantal sneetjes pizza verhogen. Stel dat het nut van 1 sneetje 10 is, dat van 2 18 is, dat van 3 24 is en dat van 4 28 is. Laten we deze getallen uitzetten op een grafiek met het nut op de verticale as en de pizza op de horizontale as (figuur 2.2).
Figuur 2.2: Grafiek en tabel van afnemend marginaal nut
|
Pizzaplakjes |
Gebruik |
Marginaal Utility |
|
1 |
10 |
|
|
2 |
18 |
8 |
|
3 |
24 |
6 |
|
4 |
28 |
4 |
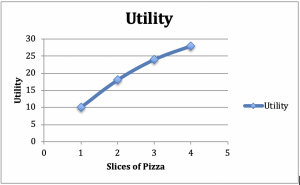
Vanuit de positieve helling van de grafiek, zien we de toename in nut van extra stukken pizza. Uit de concave vorm van de grafiek kunnen we een ander algemeen verschijnsel afleiden: Het extra nut dat de consument krijgt van elk extra stuk pizza neemt af met het aantal geconsumeerde stukken.
Het feit dat het extra nut kleiner wordt met elk extra stuk pizza, wordt het principe van afnemend marginaal nut genoemd. Dit principe geldt voor weloverwogen voorkeuren waarbij gemengde bundels de voorkeur genieten.
De marginale substitutiecoëfficiënt (MRS) is de hoeveelheid van een goed die een consument bereid is op te geven om een eenheid van een ander goed meer te krijgen. Daarom is het hetzelfde als de helling van de onverschilligheidscurve – aangezien we het tevredenheidsniveau constant houden, blijven we op dezelfde onverschilligheidscurve, we bewegen er alleen langs als we het ene goed ruilen voor het andere. Hoeveel je bereid bent te ruilen voor een ander hangt af van het marginale nut van elk goed.
Gebruik makend van ons vorige voorbeeld, als door het consumeren van een extra salade je nut met 10 toeneemt, dan zou je bij een huidige consumptie van 4 stukken pizza, 2 stukken pizza kunnen opgeven en van 28 naar 18 nutsvoorzieningen gaan. 10 meer nut van de salade en 10 minder nut door 2 stukken pizza op te geven laat het totale nut onveranderd – dus moeten we nog steeds op dezelfde indifferentiecurve zitten. Als je langs de onverschilligheidscurve beweegt, moet je de helling volgen, dat wil zeggen, je moet het goed op de verticale as opgeven voor meer van het goed op de horizontale as, wat een negatieve stijging oplevert over een positieve run.
We kunnen direct van marginaal nut naar MRS gaan door het verband tussen de twee concepten te herkennen. In ons geval wordt voor een nutsfunctie U=U(A,B) , de MRS weergegeven als:
MRS=-\frac{MU_{A}}{MU_{B}}
Merk op dat wanneer we substitueren we de vergelijking kunnen vereenvoudigen:
MRS=-\frac{MU_{A}}{MU_{B}}=-\frac{\frac{\Delta U}{\Delta A}}{\frac{\Delta U}{\Delta B}}=-\frac{\Delta B}{\Delta A}
Invoegen van de rekensom komt het neer op:
MRS=-\frac{\frac{\partieel U(A,B)}{\partieel A}}{\frac{\partieel U(A,B)}{\partieel B}}
2.5 Beleidsvraag
Wij hebben in module 1 vastgesteld dat de relevante consumentenbeslissing tussen meer gereden kilometers en andere consumptie waarschijnlijk beantwoordt aan de standaardaannames over consumentenkeuze. Daarom is het gebruik van de Cobb-Douglas nutsfunctie om een consument voor te stellen die zowel graag auto rijdt als andere goederen consumeert, en die beide als een afweging ziet (geld uitgegeven aan benzine is geld dat niet aan andere consumptiegoederen wordt uitgegeven), een goede keuze. Het heeft ook het voordeel dat het zowel aan de aannames voldoet, als flexibel is:
U(MD,C)=MD^{a}C^{\beta }
waarbij MD = gereden kilometers, en C = ander verbruik.
In feite kan de functie zelf naar reële gegevens worden gebracht waar de parameters en kunnen worden geschat voor deze markt, de markt voor gereden kilometers in de auto van de consument.
Figuur 2.3 Grafiek van de onverschilligheidscurven voor het beleidsvoorbeeld
Verkenning van de beleidsvragen:
1 . Zouden andere voorkeurstypen geschikter zijn in dit voorbeeld?
2. Wat zou waar moeten zijn voor perfecte complementen om het juiste voorkeurstype te zijn voor de analyse van dit beleid?
Wat zou waar moeten zijn voor perfecte substituten?
3. Is het, gezien het feit dat we een “typische” consument met een auto in gedachten hebben, juist om een “typische” nutsfunctie te kiezen?
4. Gissen we alleen maar of hebben we een theoretische basis om onze keuze voor “weloverwogen” voorkeuren of een Cobb-Douglas nutsfunctie te ondersteunen?
SAMENVATTING
Overzicht: Onderwerpen en verwante eindtermen
2.1 nutsfuncties
LO 2.1: Een nutsfunctie beschrijven
2.2 nutsfuncties en typische voorkeuren
LO 2.2: Identificeer nutsfuncties op basis van de typische voorkeuren die ze vertegenwoordigen
2.3 Utility Functions and Indifference Curve Maps
LO 2.3: Leg uit hoe je een indifference curve uit een nutsfunctie afleidt
2.4 Finding Marginal Utility and Marginal Rate of Substitution
LO 2.4: Leid het marginale nut en de MRS af voor typische nutsfuncties.
2.5. Beleidsvraag
Leren: Kernbegrippen en grafieken
Bi-variate functies
Cardinal
Contour line
Diminishing marginal utility
Functie
Marginal rate of substitution (MRS)
Marginal utility
Ordinale
Univariate functies
Util
Gebruiksfunctie
Grafieken
3D nutsfunctie en contourlijn
Vergelijkingen
Cobb-Douglas
Perfecte aanvullingen
Perfecte substituten