In deze les laten we een eenvoudige strategie zien voor het oplossen van het volgende probleem: hoe vind je de oppervlakte van een gelijkbenige driehoek.
Laten we een aantal eigenschappen die we tot nu toe hebben bewezen in de praktijk brengen, in het volgende meetkundeprobleem:
Probleem
In een gelijkbenige driehoek, ΔABC, met beenlengte 10, is de hoogte tot de basis gelijk aan tweederde van de basis. Bereken de oppervlakte van de driehoek.
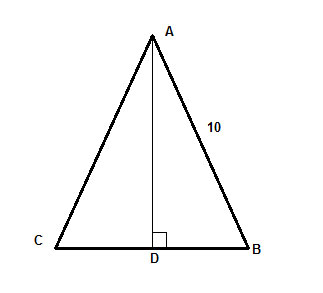
Strategie
Om dit probleem op te lossen, werken we terug naar wat we moeten doen.
We moeten de oppervlakte van de driehoek vinden, waarvan we weten dat die gegeven wordt door de formule (basis maal hoogte)/2.
Een probleem dat we hebben, is dat we noch de basislengte noch de hoogte kennen. Maar we krijgen wel het verband tussen beide, en dat is de hint voor wat we moeten doen. Laten we de lengte van de basis, BC, x noemen.
Dan weten we dat de hoogte, AD, 2x/3 is, zoals gegeven in het probleem.
Dus het antwoord dat we zoeken is (basis maal hoogte)/2, of x maal 2x/3, gedeeld door twee.
Maar hoe vinden we x? Er zijn nog twee dingen die we nog niet hebben gebruikt: de lengte van de poot (10) en het feit dat het een gelijkbenige driehoek is. We moeten deze twee dingen waarschijnlijk gebruiken om het probleem op te lossen.
Laten we de eigenschappen van gelijkbenige driehoeken eens bekijken. Een ding dat onmiddellijk in gedachten moet springen is dat, zoals we hebben laten zien, in een gelijkbenige driehoek, de hoogte tot de basis de basis in tweeën deelt, dus CD=DB=x/2.
Eindelijk is AD de hoogte, wat betekent dat de hoek ∠ADC een rechte hoek is, en we hebben een rechthoekige driehoek, ΔADC, waarvan we de schuine zijde kennen (10) en kunnen gebruiken om de benen te vinden met behulp van de stelling van Pythagoras, c2 =a2+b2,
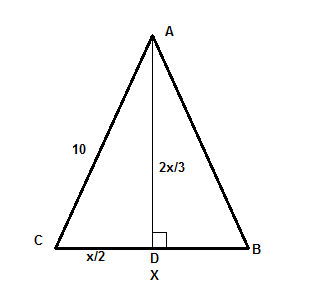
waarbij c= 10 , a = x/2 en b=2x/3 . En we zijn klaar, de rest is gewoon algebraïsch oplossen voor x.
Bewijs: oppervlakte van een gelijkbenige driehoek
(1) ΔADC is rechthoekige driehoek //gegeven, want AD is de hoogte tot de basis
(2) AC2 =CD2 + AD2 //Pythagoreïsche stelling
(3) AC= 10 //gegeven
(4) CB = x
(5) CD = x/2 /Hoogte tot basis in gelijkbenige driehoek snijdt de basis
(6) AD = 2x/3 //gegeven
(7) 102 = (x/2)2 + (2x/3)2 /substitueer in (2)
(8) 100 = x2/4+4×2/9 //simplify
(9) 100*36 = 9×2 +16×2 //multiply both sides by 36
(10) 100*36 = 25×2 //collect similar terms