Een beknopte inleiding tot de logica

9.1 Een historisch voorbeeld

De filosoof David Hume (1711-1776) wordt herinnerd als een briljant sceptisch empiricus. Iemand is een scepticus over een onderwerp als die persoon zowel zeer strenge normen heeft voor wat kennis over dat onderwerp inhoudt, als ook gelooft dat we niet aan die strenge normen kunnen voldoen. Empirisme is de opvatting dat wij hoofdzakelijk kennis vergaren door ervaring, in het bijzonder ervaringen van onze zintuigen. In zijn boek An Inquiry Concerning Human Understanding zet Hume zijn principes voor kennis uiteen, en adviseert ons vervolgens om onze bibliotheken op te ruimen:

Wanneer we bibliotheken doorzoeken, overtuigd van deze principes, wat voor ravage moeten we dan aanrichten? Als we bijvoorbeeld een boek over goddelijkheid of schoolmetafysica in onze hand nemen, laten we ons dan afvragen: Bevat het enige abstracte redenering over hoeveelheid of getal? Nee. Bevat het enige experimentele redenering over feitelijke zaken en bestaan? Nee. Gooi het dan in de vlammen, want het kan niets anders bevatten dan drogredenen en illusies.

Hume was van mening dat de enige bronnen van kennis logische of wiskundige redeneringen waren (die hij hierboven “abstracte redeneringen betreffende hoeveelheid of getal” noemt) of zintuiglijke ervaring (“experimentele redeneringen betreffende materie van feit en bestaan”). Hume redeneert dat elke bewering die niet gebaseerd is op de ene of de andere methode waardeloos is.

We kunnen Hume’s argument op de volgende manier reconstrueren. Veronderstel t is één of ander onderwerp waarover wij beweren kennis te hebben. Veronderstel dat wij deze kennis niet uit ervaring of logica hebben verkregen. In het Engels geschreven, kunnen wij zijn argument op de volgende manier reconstrueren:

Wij hebben kennis over t als en slechts als onze beweringen over t door experimenteel redeneren of door logica of wiskunde zijn geleerd.

Onze beweringen over t zijn niet geleerd uit experimenteel redeneren.

Onze beweringen over t zijn niet geleerd uit logica of wiskunde.

We hebben geen kennis over t.

Wat betekent die zinsnede “als en alleen als”? Filosofen denken dat het, en verschillende synonieme zinnen, vaak worden gebruikt in redeneringen. Als we “als en alleen” nu even buiten beschouwing laten, kunnen we de volgende vertaalsleutel gebruiken om het argument op te schrijven in een mengeling van onze propositielogica en het Engels.

P: Wij hebben kennis over t.

Q: Onze beweringen over t zijn geleerd uit experimenteel redeneren.

R: Onze beweringen over t zijn geleerd uit de logica of de wiskunde.

En zo hebben we:

P als en slechts als (QvR)

¬Q

¬R

¬P

Onze taak is om aan onze logische taal een equivalent toe te voegen voor “als en slechts als”. Dan kunnen we deze herformulering van Hume’s argument evalueren.

9.2 De biconditie

Voordat we een symbool introduceren dat synoniem is met “als en alleen als”, en dan de syntaxis en semantiek ervan uiteenzetten, moeten we beginnen met een observatie. Een zin als “P als en slechts als Q” lijkt een verkorte manier te zijn om te zeggen “P als Q en P slechts als Q”. Zodra we dit opmerken, hoeven we niet te proberen om de betekenis van “if and only if” te achterhalen met behulp van ons deskundig begrip van het Engels. In plaats daarvan kunnen we de betekenis van “als en alleen als” bepalen aan de hand van onze reeds strenge definities van “als”, “en”, en “alleen als”. Concreet wordt “P als Q en P alleen als Q” vertaald met “((Q→P)^(P→Q))”. (Als dit onduidelijk voor u is, ga dan terug en bekijk paragraaf 2.2.) Laten we nu een waarheidstabel maken voor deze formule.

P	Q	(Q → P)	(P → Q)	((Q→P)^(P→Q))
T	T	T	T	T
T	F	T	F	F
F	T	F	T	F
F	F	T	T	T

We hebben de semantiek voor “als en alleen als” geregeld. We kunnen nu een nieuw symbool voor deze uitdrukking introduceren. Het is gebruikelijk om de dubbele pijl, “↔”, te gebruiken. We kunnen nu de syntaxis en semantiek van “↔” uitdrukken.

Als Φ en Ψ zinnen zijn, dan

(Φ↔Ψ)

is een zin. Dit soort zinnen wordt meestal een “biconditie” genoemd.

De semantiek wordt gegeven door de volgende waarheidstabel.

Φ	Ψ	(Φ↔Ψ)
T	T	T
T	F	F
F	T	F
F	F	T

Een verheugend resultaat van onze uiteenzetting van de biconditie is dat het ons in staat stelt om het syntactische begrip logische equivalentie beknopt uit te leggen. We zeggen dat twee zinnen Φ en Ψ “equivalent” of “logisch equivalent” zijn als (Φ↔Ψ) een stelling is.

9.3 Alternatieve zinnen

In het Engels blijken er verschillende zinnen te zijn die gewoonlijk dezelfde betekenis hebben als de biconditional. Elk van de volgende zinnen zou vertaald worden als (P↔Q).

P if and only if Q.

P just in case Q.

P is noodzakelijk en voldoende voor Q.

P is equivalent aan Q.

9.4 Redeneren met de biconditional

Hoe kunnen we redeneren met behulp van een biconditional? Op het eerste gezicht lijkt het weinig houvast te bieden. Als ik weet dat (P↔Q), dan weet ik dat P en Q dezelfde waarheidswaarde hebben, maar uit die zin alleen weet ik niet of ze allebei waar of allebei onwaar zijn. Niettemin kunnen we gebruik maken van de semantiek voor de biconditional om op te merken dat als we ook de waarheidswaarde kennen van een van de zinnen die samen de biconditional vormen, we dan de waarheidswaarde van de andere zin kunnen afleiden. Dit suggereert een eenvoudige reeks regels. Dit zijn in feite vier regels, maar we groeperen ze onder één naam, “equivalentie”:

en

en

en

Wat als we in plaats daarvan proberen een biconditie aan te tonen? Hier kunnen we teruggrijpen op het inzicht dat de biconditie (Φ↔Ψ) equivalent is aan ((Φ→Ψ)^(Ψ→Φ)). Als we zowel (Φ→Ψ) als (Ψ→Φ) kunnen bewijzen, weten we dat (Φ↔Ψ) waar moet zijn.

We kunnen deze regel “biconditie” noemen. Hij heeft de volgende vorm:

(Φ→Ψ)

(Ψ→Φ)

(Φ↔Ψ)

Dit betekent dat we, wanneer we een biconditie willen bewijzen, vaak twee conditionele afleidingen zullen doen om twee conditionalen af te leiden, en dan de biconditie regel zullen gebruiken. Dat wil zeggen dat veel bewijzen van bicondities de volgende vorm hebben:

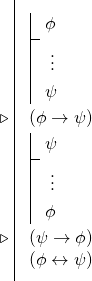
9.5 Terug naar Hume

We kunnen nu zien of we in staat zijn om Hume’s argument te bewijzen. Gegeven nu het nieuwe biconditiële symbool, kunnen we een direct bewijs beginnen met onze drie premissen.

We hebben al opgemerkt dat we denken dat (QvR) onwaar is omdat ¬Q en ¬R. Laten we dus ¬(QvR) bewijzen. Deze zin kan niet rechtstreeks worden bewezen, gezien de premissen die we hebben; en hij kan niet worden bewezen met een voorwaardelijk bewijs, aangezien hij niet voorwaardelijk is. Laten we dus een indirect bewijs proberen. We geloven dat ¬(QvR) waar is, dus we zullen de ontkenning hiervan aannemen en een tegenspraak aantonen.

Hume’s argument, althans zoals we het gereconstrueerd hebben, is geldig.

Is Hume’s argument steekhoudend? Of het juist is hangt af van de eerste premisse hierboven (aangezien de tweede en derde premissen abstracties zijn over één of ander onderwerp t). Meer bepaald hangt het af van de bewering dat wij kennis over iets hebben enkel in het geval wij het met experiment of logica kunnen aantonen. Hume beweert dat wij teksten met beweringen die niet uit experimenten en observaties, of uit logica en wiskunde voortkomen, moeten wantrouwen – en zelfs verbranden. Maar overweeg deze bewering: wij hebben kennis over een onderwerp t als en slechts als onze beweringen over t uit experimenten zijn geleerd of onze beweringen over t uit logica of wiskunde zijn geleerd.

Ontdekte Hume deze bewering door experimenten? Of ontdekte hij het door logica? Welk lot zou Hume’s boek ondergaan, als we zijn raad opvolgden?

9.6 Enkele voorbeelden

Het kan nuttig zijn enkele stellingen te bewijzen die gebruik maken van de biconditional, om te illustreren hoe we met de biconditional kunnen redeneren.

Hier is een nuttig principe. Als twee zinnen dezelfde waarheidswaarde hebben als een derde zin, dan hebben ze dezelfde waarheidswaarde als elkaar. We stellen dit als (((P↔Q)^(R↔Q))→(P↔R)). Laten we, om het redeneren met de biconditie te illustreren, deze stelling bewijzen.

Deze stelling is een voorwaardelijke, dus zal ze een voorwaardelijke afleiding vereisen. Het gevolg van de voorwaardelijke is een biconditionele, dus we verwachten twee voorwaardelijke afleidingen nodig te hebben, een om (P→R) te bewijzen en een om (R→P) te bewijzen. Het bewijs zal er als volgt uitzien. Bestudeer het aandachtig.

We hebben het al eerder gehad over de principes die we associëren met de wiskundige Augustus De Morgan (1806-1871), en die tegenwoordig “De Morgan’s Wetten” of de “De Morgan Equivalences” worden genoemd. Het gaat om de erkenning dat ¬(PvQ) en (¬P^¬Q) equivalent zijn, en ook dat ¬(P^Q) en (¬Pv¬Q) equivalent zijn. Deze kunnen we nu met de biconditie uitdrukken. Dit zijn stellingen van onze logica:

(¬(PvQ)↔(¬P^¬Q))

(¬(P^Q)↔(¬Pv¬Q))

We zullen de tweede van deze stellingen bewijzen. Dit is misschien het moeilijkste bewijs dat we gezien hebben; het vereist geneste indirecte bewijzen, en een behoorlijke hoeveelheid slimheid om te vinden wat de relevante tegenspraak zal zijn.

9.7 Stellingen gebruiken

Elke zin van onze logica is, in semantische termen, een van de drie soorten. Het is ofwel een tautologie, ofwel een tegenstrijdige zin, ofwel een contingente zin. We hebben reeds “tautologie” (een zin die waar moet zijn) en “tegenstrijdige zin” (een zin die onwaar moet zijn) gedefinieerd. Een voorwaardelijke zin is een zin die noch een tautologie noch een tegenstrijdige zin is. Een voorwaardelijke zin is dus een zin die waar zou kunnen zijn, of die onwaar zou kunnen zijn.

Hier volgt een voorbeeld van elk soort zin:

(Pv¬P)

(P↔¬P)

P

De eerste is een tautologie, de tweede is een tegenstrijdige zin, en de derde is voorwaardelijk. We kunnen dit zien met een waarheidstabel.

P	¬P	(Pv¬P)	(P↔¬P)	P
T	F	T	F	T
F	T	T	F	F

Merk op dat de negatie van een tautologie een contradictie is, de negatie van een contradictie een tautologie is, en de negatie van een voorwaardelijke zin een voorwaardelijke zin is.

¬(Pv¬P)

¬(P↔¬P)

¬P

P	¬P	(Pv¬P)	¬(Pv¬P)	(P↔¬P)	¬(P↔¬P)
T	F	T	F	F	T
F	T	T	F	T

Een moment van bezinning leert dat het een regelrechte ramp zou zijn als ofwel een tegenstrijdige zin ofwel een contingente zin een stelling van onze propositionele logica zou zijn. Onze logica is ontworpen om alleen geldige argumenten te produceren. Argumenten die geen premissen hebben, zo stelden wij vast, moeten conclusies hebben die waar moeten zijn (nogmaals, dit volgt uit het feit dat een zin die bewezen kan worden zonder premissen, bewezen kan worden met om het even welke premissen, en dat de zin dus maar beter waar kan zijn, welke premissen we ook gebruiken). Als een stelling tegenstrijdig zou zijn, dan zouden we weten dat we een onwaarheid kunnen bewijzen. Als een stelling contingent zou zijn, dan zouden we soms een onwaarheid kunnen bewijzen (dat wil zeggen, we zouden een zin kunnen bewijzen die onder bepaalde voorwaarden onwaar is). En, gegeven het feit dat we indirecte afleiding als bewijsmethode hebben aangenomen, volgt daaruit dat zodra we een tegenspraak of een tegenstrijdige zin in een argument hebben, we alles kunnen bewijzen.

Stellingen kunnen ons in argumenten zeer van pas komen. Stel dat we weten dat noch Smith noch Jones naar Londen zullen gaan, en we willen daarom bewijzen dat Jones niet naar Londen zal gaan. Als we onszelf toestaan een van de stellingen van De Morgan te gebruiken, kunnen we snel werk maken van het argument. Neem de volgende sleutel aan.

P: Smith zal naar Londen gaan.

Q: Jones zal naar Londen gaan.

En we hebben het volgende argument:

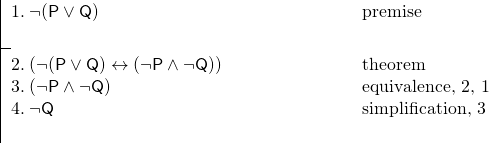
Dit bewijs is heel gemakkelijk gemaakt door ons gebruik van de stelling op regel 2.

Er zijn hierover twee dingen op te merken. Ten eerste moeten we onszelf toestaan dit te doen, want als we weten dat een zin een stelling is, dan weten we dat we die stelling kunnen bewijzen in een deelbewijs. Dat wil zeggen, we zouden regel 2 hierboven kunnen vervangen door een lang subbewijs dat bewijst (¬(P v Q)↔(¬P ^ ¬Q)), dat we dan zouden kunnen gebruiken. Maar als we zeker weten dat (¬(P v Q)↔(¬P ^ ¬Q)) een stelling is, hoeven we dit bewijs niet steeds opnieuw te doen, elke keer dat we van de stelling gebruik willen maken.

Het tweede probleem dat we moeten onderkennen is subtieler. Er zijn oneindig veel zinnen van de vorm van onze stelling, en die zouden we ook moeten kunnen gebruiken. Bijvoorbeeld, de volgende zinnen zouden elk een bewijs hebben dat identiek is aan ons bewijs van de stelling (¬(P v Q)↔(¬P ^ ¬Q)), behalve dat de letters anders zouden zijn:

(¬(R v S) ↔ (¬R ^ ¬S))

(¬(T v U) ↔ (¬T ^ ¬U))

(¬(V v W) ↔ (¬V ^ ¬W))

Dit ligt hopelijk voor de hand. Neem het bewijs van (¬(P v Q)↔(¬P ^ ¬Q)), en vervang in dat bewijs elk geval van P door R en elk geval van Q door S, en je zou een bewijs hebben van (¬(R v S)↔(¬R ^ ¬S)).

Maar hier is iets dat misschien minder duidelijk is. Elk van het volgende kan worden beschouwd als vergelijkbaar met de stelling (¬(P v Q)↔(¬P ^ ¬Q)).

(¬((P^Q) v (R^S))↔(¬(P^Q) ^ ¬(R^S)))

(¬(T v (Q v V))↔(¬T ^ ¬(Q v V))

(¬((Q↔P) v (¬R→¬Q))↔(¬(Q↔P) ^ ¬(¬R→¬Q)))

Voorbeeld, als men een bewijs nam van (¬(P v Q)↔(¬P ^ ¬Q)) en elk begingeval van P verving door (Q↔P) en elk begingeval van Q door (¬R→¬Q), dan zou men een bewijs hebben van de stelling (¬((Q↔P) v (¬R→¬Q))↔(¬(Q↔P) ^ ¬(¬R→¬Q)).

We zouden dit inzicht op twee manieren kunnen vastleggen. We zouden stellingen van onze metataal kunnen formuleren en kunnen toestaan dat deze stellingen instanties hebben. Zo zouden we (¬(Φ v Ψ) ↔ (¬Φ ^ ¬Ψ)) als een metataalstelling kunnen nemen, waarbij we elke Φ door een zin en elke Ψ door een zin kunnen vervangen en zo een bepaalde instantie van een stelling krijgen. Een alternatief is om toe te staan dat uit een stelling door substitutie andere stellingen kunnen worden afgeleid. Gemakshalve zullen we deze tweede strategie volgen.

Onze regel zal als volgt zijn. Als we eenmaal een stelling bewezen hebben, kunnen we die te allen tijde in een bewijs aanhalen. Onze rechtvaardiging is dat de bewering een stelling is. We staan substitutie van elke atomaire zin in de stelling door elke andere zin toe als en slechts als we elk initieel geval van die atomaire zin in de stelling door dezelfde zin vervangen.

Voordat we een voorbeeld beschouwen, is het nuttig enkele nuttige stellingen op te sommen. Er zijn oneindig veel stellingen in onze taal, maar deze tien zijn vaak zeer nuttig. Een paar hebben we bewezen. De andere kunnen als oefening bewezen worden.

T1 (P v ¬P)

T2 (¬(P→Q) ↔ (P^¬Q))

T3 (¬(P v Q) ↔ (¬P ^ ¬Q))

T4 ((¬P v ¬Q) ↔ ¬(P ^ Q))

T5 (¬(P ↔ Q) ↔ (P ↔ ¬Q))

T6 (¬P → (P → Q))

T7 (P → (Q → P))

T8 ((P→(Q→R)) → ((P→Q) → (P→R)))

T9 ((¬P→¬Q) → ((¬P→Q) →P))

T10 ((P→Q) → (¬Q→¬P))

Een paar voorbeelden zullen het voordeel van het gebruik van stellingen duidelijk maken. Beschouw een ander argument, voortbouwend op het argument hierboven. Wij weten dat noch het geval is dat als Smith naar Londen gaat, hij ook naar Berlijn zal gaan, noch het geval is dat als Jones naar Londen gaat, hij ook naar Berlijn zal gaan. Wij willen bewijzen dat het niet het geval is dat Jones naar Berlijn zal gaan. We voegen het volgende toe aan onze sleutel:

R: Smith zal naar Berlijn gaan.

S: Jones zal naar Berlijn gaan.

En we hebben het volgende argument:

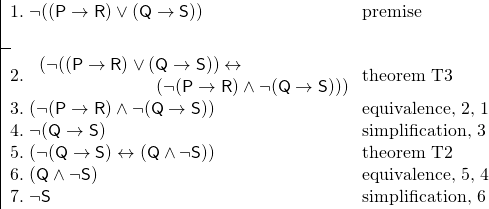
Het gebruik van stellingen maakt dit bewijs veel korter dan het anders zou zijn. Ook maken stellingen een bewijs vaak gemakkelijker te volgen, omdat we de stellingen herkennen als tautologieën – als zinnen die waar moeten zijn.

9.8 Problemen

1. Bewijs dat elk van de volgende argumenten geldig is.

1. Vooronderstellingen: P, ¬Q. Conclusie: ¬(P↔Q).
2. Voorstellingen: (¬PvQ), (Pv¬Q). Conclusie: (P↔Q).
3. Premissen: (P↔Q), (R↔S) . Conclusie: ((P^R)↔(Q^S)).

1. Voer elk van de volgende stellingen aan.

1. T1
2. T2
3. T5
4. T6
5. T7
6. T8
7. T9
8. ((P^Q)↔¬(¬Pv¬Q))
9. ((P→Q)↔¬(P^¬Q))

1. Schrijf in normaal spreektaal Engels je eigen geldige argument met minstens twee premissen, waarvan er minstens één een bicondicional is. Je argument moet gewoon een alinea zijn (geen geordende lijst van zinnen of iets anders dat op formele logica lijkt). Vertaal het in propositielogica en bewijs dat het geldig is.
2. In normaal spreektaal Engels, schrijf je eigen geldige argument met ten minste twee premissen, en met een conclusie die een bicondicional is. Je argument moet gewoon een alinea zijn (geen geordende lijst van zinnen of iets anders dat er formeel uitziet als logica). Vertaal het in propositionele logica en bewijs dat het geldig is.