Antwoord 7 – 7 – 7 = 73 Dit is “zeven tot de derde macht verheven.”

Inzicht in exponenten en vierkantswortels

Leerdoel(en)

– Uitdrukkingen evalueren die exponenten bevatten.

– Herhaalde factoren schrijven met behulp van exponentiële notatie.

– Een vierkantswortel vinden van een perfect kwadraat.

Exponenten bieden een speciale manier om herhaalde vermenigvuldiging te schrijven. Getallen die op deze manier worden geschreven hebben een specifieke vorm, waarbij elk deel belangrijke informatie geeft over het getal. Getallen schrijven met exponenten kan ook veel ruimte besparen. De omgekeerde bewerking van het vermenigvuldigen van een getal met zichzelf wordt het vinden van de vierkantswortel van een getal genoemd. Deze bewerking is nuttig bij problemen over de oppervlakte van een vierkant.

Exponentiële notatie is een speciale manier om herhaalde factoren te schrijven, bijvoorbeeld 7 – 7. Exponentiële notatie bestaat uit twee delen. Het ene deel van de notatie wordt de basis genoemd. De basis is het getal dat met zichzelf wordt vermenigvuldigd. Het andere deel van de notatie is de exponent, of macht. Dit is het kleine getal dat hoog rechts van het grondtal staat. De exponent, of macht, geeft aan hoeveel keer het grondtal moet worden gebruikt als factor in de vermenigvuldiging. In het voorbeeld kan 7 – 7 geschreven worden als 72, 7 is de basis en 2 is de exponent. De exponent 2 betekent dat er twee factoren zijn.

72 = 7 – 7 = 49

Je kunt 72 lezen als “zeven in het kwadraat”. Dit komt omdat het vermenigvuldigen van een getal met zichzelf “het kwadrateren van een getal” wordt genoemd. Op dezelfde manier wordt het verheffen van een getal tot een macht van 3 “het kwadrateren van het getal” genoemd. Je kunt 73 lezen als “zeven in het kwadraat”.

Je kunt 25 lezen als “twee tot de vijfde macht” of “twee tot de macht van vijf”. Lees 84 als “acht tot de vierde macht” of “acht tot de vierde macht”. Deze notatie kan worden gebruikt om elk getal in exponentiële notatie te lezen. Hoewel 63 meestal wordt gelezen als “zes tot de derde macht” of “zes tot de derde macht”, kan het ook worden gelezen als “zes tot de derde macht” of “zes tot de derde macht”.

Om de waarde te vinden van een getal dat in exponentiële vorm is geschreven, herschrijft u het getal als herhaalde vermenigvuldiging en voert u de vermenigvuldiging uit. Hieronder staan twee voorbeelden.

Vind de waarde van 43.

A) 12

B) 64

C) 256

D) 43

Herhaalde vermenigvuldiging schrijven in exponentiële notatie kan tijd en ruimte besparen. Neem het voorbeeld 5 – 5 – 5 – 5. We kunnen exponentiële notatie gebruiken om deze herhaalde vermenigvuldiging te schrijven als 54. Omdat 5 vermenigvuldigd wordt, wordt het als basis geschreven. Omdat het grondtal 4 keer wordt gebruikt in de vermenigvuldiging, is de exponent 4. De uitdrukking 5 – 5 – 5 – 5 kan in steno exponentiële notatie worden herschreven als 54 en wordt gelezen als “vijf tot de vierde macht” of “vijf tot de macht van 4.”

Om herhaalde vermenigvuldigingen van hetzelfde getal in exponentiële notatie te schrijven, schrijf je eerst het getal dat wordt vermenigvuldigd als het grondtal. Tel vervolgens hoe vaak dat getal in de vermenigvuldiging wordt gebruikt, en schrijf dat getal als exponent. Zorg ervoor dat je de getallen telt, niet de vermenigvuldigingstekens, om de exponent te bepalen.

Schrijf 10 – 10 – 10 – 10 – 10 – 10 in exponentiële notatie.

A) 1.000.000

B) 60

C) 105

D) 106

Zoals je eerder zag, wordt 52 “vijf in het kwadraat” genoemd. “Vijf in het kwadraat” betekent vijf met zichzelf vermenigvuldigen. In de wiskunde noemen we het vermenigvuldigen van een getal met zichzelf “kwadrateren” van het getal. Het resultaat van het kwadrateren van een geheel getal noemen we een kwadraat of een perfect kwadraat. Een perfect kwadraat is elk getal dat kan worden geschreven als een geheel getal verheven tot de macht 2. Bijvoorbeeld, 9 is een perfect kwadraat. Een kwadraatgetal kan worden weergegeven als een vierkant, zoals hieronder. We zien dat 1, 4, 9, 16, 25 en 36 voorbeelden zijn van perfecte kwadraten.

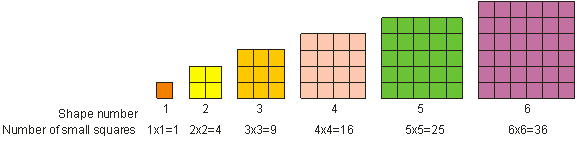
Om een getal te kwadrateren, vermenigvuldigt u het getal met zichzelf. 3 kwadraat = 32 = 3 – 3 = 9.

Hieronder staan nog enkele voorbeelden van perfecte kwadraten.

De omgekeerde bewerking van het kwadrateren van een getal wordt het vinden van de vierkantswortel van een getal genoemd. Een vierkantswortel vinden is zoiets als vragen: “Welk getal vermenigvuldigd met zichzelf geeft me dit getal?” De vierkantswortel van 25 is 5, want 5 vermenigvuldigd met zichzelf is gelijk aan 25. Vierkantswortels worden geschreven met een wiskundig symbool, radicaalteken genaamd, dat er zo uitziet: . De “vierkantswortel van 25” wordt geschreven als .

Vind .

A) 6

B) 18

C) 72

D) 7

Exponentiële notatie is een stenografische manier om herhaalde vermenigvuldigingen van eenzelfde getal te schrijven. Een getal geschreven in exponentiële notatie heeft een basis en een exponent, en elk van deze delen geeft informatie voor het vinden van de waarde van de uitdrukking. De basis vertelt welk getal herhaaldelijk wordt vermenigvuldigd, en de exponent vertelt hoeveel keer de basis wordt gebruikt in de vermenigvuldiging. De exponenten 2 en 3 hebben speciale namen. Een basis verheffen tot een macht van 2 heet “kwadrateren” van een getal. Een basis verheffen tot een macht van 3 heet een getal “verdrievoudigen”. Het omgekeerde van het kwadrateren van een getal is het vinden van de vierkantswortel van een getal. Om de vierkantswortel van een getal te vinden, vraag je je af: “Welk getal kan ik met zichzelf vermenigvuldigen om dit getal te krijgen?”