
A Questão Política: Crédito Fiscal para Compra de Automóvel Híbrido – É a Melhor Escolha do Governo para Reduzir o Consumo de Combustível e as Emissões de Carbono?
Os residentes dos EUA e o governo estão preocupados com a dependência do petróleo estrangeiro importado e a liberação de carbono na atmosfera. Em 2005, o Congresso aprovou uma lei para fornecer aos consumidores créditos fiscais para a compra de carros elétricos e híbridos.
Este crédito fiscal pode parecer uma boa escolha política, mas é caro porque reduz diretamente a quantidade de receita que o governo dos EUA cobra. Existem abordagens mais eficazes para reduzir a dependência dos combustíveis fósseis e das emissões de carbono? Como decidimos qual é a melhor política? Para responder a esta pergunta, os legisladores precisam prever com alguma precisão como os consumidores responderão a essa política fiscal antes que esses legisladores gastem milhões de dólares federais.
Podemos aplicar o conceito de utilidade a essa pergunta de política. Neste módulo, vamos estudar as funções de utilidade e utilidade. Poderemos então usar uma função de utilidade apropriada para derivar curvas de indiferença que descrevem a nossa questão de política.
Explorar a questão de política
Suponha que o crédito fiscal para subsidiar a compra de carros híbridos é extremamente bem sucedido e duplica a economia média de combustível de todos os carros nas estradas dos EUA – um resultado que claramente não é realista, mas útil para as nossas discussões subsequentes. O que você acha que aconteceria com o consumo de combustível de todos os motoristas dos EUA? O governo deveria esperar que o consumo de combustível e as emissões de carbono dos automóveis diminuíssem para metade em resposta? Porquê ou porque não?
2.1 Funções utilitárias
LO 2.1: Descreva uma função de utilidade.
2.2 Funções de utilidade e preferências típicas
LO 2.2: Identificar funções de utilidade baseadas nas preferências típicas que elas representam.
2.3 Relacionando Funções de Utilidade e Curvas de Indiferença Mapas
LO 2.3: Explicar como derivar uma curva de indiferença de uma função de utilidade.
2.4 Encontrando Utilidade Marginal e Taxa Marginal de Substituição
LO 2.4: Derivar utilidade marginal e MRS para funções de utilidade típicas.
2.5. Pergunta de política
2.1 Funções utilitárias
LO1: Descreva uma função utilitária.
As nossas preferências permitem-nos fazer comparações entre os diferentes pacotes de consumo e escolher os pacotes preferidos. Poderíamos, por exemplo, determinar a ordem de classificação de todo um conjunto de pacotes com base em nossas preferências. Uma função de utilidade é uma função matemática que classifica os pacotes de bens de consumo atribuindo um número a cada um deles onde números maiores indicam os pacotes preferidos. As funções utilitárias têm as propriedades que identificamos no Módulo 1 em relação às preferências. Isto é: eles são capazes de pedir pacotes, são completos e transitivos, mais é preferível a menos e, em casos relevantes, os pacotes mistos são melhores.
O número que a função utilidade atribui a um pacote específico é conhecido como utilidade, a satisfação que um consumidor obtém de um pacote específico. O número da utilidade para cada pacote não significa nada em termos absolutos; não há uma escala uniforme contra a qual medimos a satisfação. É apenas em termos relativos: podemos usar a utilidade para determinar quais pacotes são preferidos em relação a outros.
Se a utilidade do pacote A for maior que a utilidade do pacote B, equivale a dizer que um consumidor prefere o pacote A ao pacote B. As funções de utilidade, portanto, classificam as preferências do consumidor atribuindo um número a cada pacote. . Podemos usar uma função de utilidade para desenhar os mapas de curvas de indiferença descritos no Módulo 1. Como todos os pacotes na mesma curva de indiferença proporcionam a mesma satisfação, e portanto nenhum é preferido, cada pacote tem a mesma utilidade. Podemos portanto desenhar uma curva de indiferença determinando todos os bundles que retornam o mesmo número da função utilidade.
Economistas dizem que funções utilitárias são ordinais ao invés de cardinais. Ordinal significa que as funções utilitárias só classificam os bundles – elas apenas indicam qual é melhor, não o quanto melhor do que outro bundle. Suponha, por exemplo, que uma função de utilidade indica que o pacote A retorna 10 utils e o pacote B 20 utils. Não dizemos que o pacote B é duas vezes melhor, ou 10 utils melhor, apenas que o consumidor prefere o pacote B. Por exemplo, suponha que uma amiga entrou numa corrida e lhe disse que ela chegou em terceiro. Esta informação é ordinal: Você sabe que ela foi mais rápida que o quarto classificado e mais lenta que o segundo classificado. Você só conhece a ordem em que os corredores terminaram. Os tempos individuais são cardeais: Se o primeiro classificado terminou a corrida em exatamente uma hora e a sua amiga terminou em uma hora e seis minutos, você sabe que a sua amiga foi 10% mais lenta que a corredora mais rápida. porque as funções utilitárias são ordinais muitas funções utilitárias diferentes podem representar as mesmas preferências. Isto é verdade desde que a encomenda seja preservada.
Toma por exemplo a função utilitária U que descreve as preferências de excesso de bens A abd B: U(A,B). Podemos aplicar qualquer transformação monotónica positiva a esta função (o que significa, essencialmente, que não alteramos a ordenação) e a nova função que criámos irá representar as mesmas preferências. Por exemplo, podemos multiplicar uma constante positiva, α , ou adicionar uma constante positiva ou negativa, β . Assim αU(A,B)+β representa exactamente as mesmas preferências que U(A,B) porque vai encomendar os pacotes exactamente da mesma forma. Este fato é bastante útil porque às vezes aplicando uma transformação monotônica positiva de uma função utilitária facilita a solução de problemas.
2.2 Funções utilitárias e preferências típicas
LO2: Identificar funções de utilidade baseadas nas preferências típicas que representam
Considerar feixes de maçãs, A, e bananas, B. Uma função de utilidade que descreve as preferências de Isaac para feixes de maçãs e bananas é a função U(A,B). Mas quais são as preferências particulares de Isaac para os feixes de maçãs e bananas? Suponha que Isaac tem preferências razoavelmente padrão para maçãs e bananas que levam às nossas típicas curvas de indiferença: Ele prefere mais a menos, e ele gosta de variedade. Uma função de utilidade que representa estas preferências poderia ser:
U(A,B) = AB
Se maçãs e bananas são complementos perfeitos nas preferências de Isaac, a função de utilidade seria algo parecido com isto:
U(A,B) = MIN,
onde a função MIN simplesmente atribui o menor dos dois números como valor da função.
Se maçãs e bananas são substitutos perfeitos, a função utilitária é aditiva e pareceria algo assim:
U(A,B) = A + B
Uma classe de funções utilitárias conhecidas como funções utilitárias Cobb-Douglas são muito comumente usadas em economia por duas razões:
1. Elas representam preferências ‘bem-comportadas’, tais como mais é melhor e preferência pela variedade.
2. Elas são muito flexíveis e podem ser ajustadas para se ajustarem a dados do mundo real muito facilmente.
Cobb-Douglas funções utilitárias têm esta forma:
U(A,B) = AαBβ
Porque transformações monotônicas positivas representam as mesmas preferências, uma dessas transformações pode ser usada para definir α + β = 1 , o que mais tarde veremos é uma condição conveniente que simplifica alguma matemática no problema de escolha do consumidor.
Outra forma de transformar a função utilidade de uma forma útil é pegar o log natural da função, o que cria uma nova função que se parece com isto:
U(A,B) = αln(A) + βln(B)
Para derivar esta equação, basta aplicar as regras dos logs naturais. . É importante ter em mente o nível de abstracção aqui. Normalmente não podemos fazer funções utilitárias específicas que descrevam com precisão as preferências individuais. Provavelmente nenhum de nós poderia descrever nossas próprias preferências com uma única equação. Mas desde que os consumidores em geral tenham preferências que seguem nossas suposições básicas, podemos fazer um bom trabalho para encontrar funções de utilidade que correspondam aos dados de consumo do mundo real. Veremos evidências disso mais tarde no curso.
Tabela 2.1 resume as preferências e funções utilitárias descritas nesta seção.
|
Tabela 2.1 Tipos de Preferências e Funções de Utilidade que as Representam |
||
|
PREFERÊNCIAS |
UTILIDADE FUNÇÃO |
TIPO DE FUNÇÃO DE UTILIDADE |
|
Amor da Variedade ou “Bem Comportado” |
U(A,B) = AB |
Cobb-Douglas |
|
Amor da Variedade ou “Bem Comportado” |
U(A,B) = AαBβ |
Cobb-Douglas |
|
Amor da Variedade ou “Bem Comportado” |
U(A,B) = αln(A) + βln(B) |
>
Natural Log Cobb-Douglas |
|
Complementos Perfeitos |
U(A,B) = MIN |
>
Função Sinóptica |
|
Substitutos Perfeitos |
>
U(A,B) = A + B |
Aditivo |
2.3 Funções de Utilidade Relativa e Mapas de Curvas de Indiferença
>
LO3: Explique como derivar uma curva de indiferença de uma função de utilidade
Curvas de indiferença e funções de utilidade estão diretamente relacionadas. Na verdade, como as curvas de indiferença representam graficamente as preferências e as funções de utilidade representam matematicamente as preferências, segue-se que as curvas de indiferença podem ser derivadas das funções de utilidade.
Em funções uni-variadas, a variável dependente é plotada no eixo vertical e a variável independente é plotada no eixo horizontal, como o gráfico de y=f(x). Em contraste, os gráficos de funções bi-variadas são tridimensionais, como U=U(A,B). A Figura 2.1 mostra um gráfico de U=A^\frac{1}{2}B^\frac{1}{2}. Os gráficos tridimensionais são úteis para entender como a utilidade aumenta com o aumento do consumo de A e B.
Figure 2.1 U=A^\frac{1}{2}B^\frac{1}{2}
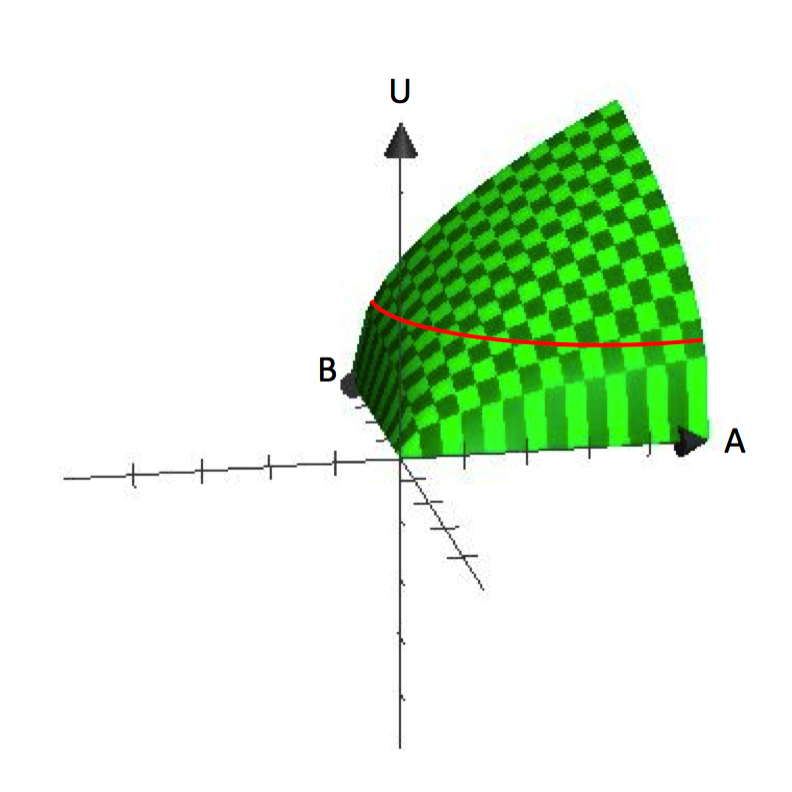
Figure 2.1 mostra claramente a suposição de que os consumidores têm preferência pela variedade. Cada feixe que contém uma quantidade específica de A e B representa um ponto na superfície. A altura vertical da superfície representa o nível de utilidade. Ao aumentar tanto A como B, um consumidor pode alcançar pontos mais altos na superfície.
Então de onde vêm as curvas de indiferença? Lembre-se que uma curva de indiferença é uma coleção de todos os pacotes que um consumidor é indiferente, em relação aos quais se deve consumir. Matematicamente, isto equivale a dizer que todos os fardos, quando colocados na função utilidade, retornam o mesmo valor funcional. Então, se definirmos um valor para a utilidade, Ū, e encontrarmos todos os bundles de A e B que geram esse valor, vamos definir uma curva de indiferença. Note que isto é equivalente a encontrar todos os bundles que levam o consumidor à mesma altura na superfície tridimensional na Figura 2.1.
Curvas de indiferença são uma representação de elevação (nível de utilidade) em uma superfície plana. Desta forma, elas são análogas a uma linha de contorno em um mapa topográfico. Levando o gráfico tridimensional de volta ao espaço bidimensional – o espaço A, B – podemos mostrar as curvas de contorno/ curvas de indiferença que representam diferentes elevações ou níveis de utilidade. Do gráfico da Figura 2.1, você já pode ver como esta função de utilidade produz curvas de indiferença que são ‘curvadas’ ou côncavas à origem.
Então as curvas de indiferença seguem diretamente das funções de utilidade e são uma maneira útil de representar as funções de utilidade em um gráfico bidimensional.
2.4 Encontrar Utilidade Marginal e Taxa Marginal de Substituição
LO4: Derivar utilidade marginal e MRS para funções utilitárias típicas.
Utilidade marginal é a utilidade adicional que um consumidor recebe ao consumir uma unidade adicional de um bem. Matematicamente expressamos isso como:
MU_{a}=\frac{\Delta \cup }{\Delta A}
ou a mudança no utilitário a partir de uma mudança na quantidade de A consumida, onde Δ representa uma mudança no valor do item. Então,
MU_{a}==frac{\Delta \cup }{\Delta A}=frac{\cup (A+\Delta A,B)-U(A,B)}{\Delta A}
Notem que quando estamos examinando a utilidade marginal do consumo de A, mantemos constante B.
Usando cálculo, a utilidade marginal é a mesma que a derivada parcial da função utilidade em relação a A:
MU_{\A}frac{\frac{\parcial U(A,B)}{\parcial A}
Considerar um consumidor que se senta para comer uma refeição de salada e pizza. Suponha que mantemos constante a quantidade de salada – uma salada de um lado com um jantar, por exemplo. Agora vamos aumentar as fatias de pizza suponha que com 1 fatia a utilidade é 10, com 2 é 18, com 3 é 24 e com 4 é 28. Vamos traçar estes números em um gráfico que tenha utilidade no eixo vertical e pizza no eixo horizontal (Figura 2.2).
Figure 2.2: Gráfico e tabela de Utilidade Marginal Diminutiva
|
Pizza Slices |
Utilidade |
Marginal Utilidade |
|
1 |
>10 |
|
|
2 |
>>18 |
8 |
|
3 |
24 |
6 |
|
4 |
28 |
4 |
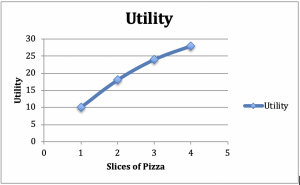
Da inclinação positiva do gráfico, podemos ver o aumento da utilidade de fatias adicionais de pizza. A partir da forma côncava do gráfico, podemos ver outro fenômeno comum: A utilidade adicional que o consumidor recebe de cada fatia adicional de pizza diminui com o número de fatias consumidas.
O fato de que a utilidade adicional fica menor com cada fatia adicional de pizza é chamado o princípio da utilidade marginal decrescente. Este princípio aplica-se às preferências bem-comportadas onde são preferidos os pacotes mistos.
Marginal rate of substitution (MRS) é a quantidade de um bem que um consumidor disposto a desistir para obter mais uma unidade de outro bem. É por isso que é a mesma coisa que a inclinação da curva de indiferença – uma vez que mantemos constante o nível de satisfação, nos mantemos na mesma curva de indiferença, apenas nos movendo ao longo dela enquanto trocamos um bem por outro. Quanto de um você está disposto a trocar por mais um de outro depende da utilidade marginal de cada um.
Usando nosso exemplo anterior, se ao consumir mais uma salada lateral sua utilidade aumenta em 10, então com um consumo atual de 4 fatias de pizza, você poderia abrir mão de 2 fatias de pizza e passar de 28 para 18 utils. Mais 10 fatias de salada e menos 10 fatias de pizza, deixando 2 fatias de pizza sem alterar a utilidade geral – por isso devemos continuar na mesma curva de indiferença. À medida que você se move ao longo da curva de indiferença, você deve estar montando a inclinação, ou seja, você deve estar abrindo mão do bem no eixo vertical por mais do bem no eixo horizontal, o que produz um aumento negativo em uma corrida positiva.
Nós podemos ir diretamente da utilidade marginal para MRS, reconhecendo a conexão entre os dois conceitos. No nosso caso, para uma função utilidade U=U(A,B) , MRS é representada como:
MRS=-\frac{MU_{A}}{MU_{B}}
Note que quando substituímos podemos simplificar a equação:
MRS=->frac{MU_{A}}{MU_{B}}=->frac{\i1}}Delta U}{Delta A}{\i}{\i1}frac{\i}{\i}Delta U}{\i}{\i1}-frac{\i}{\i}Delta B}{\i}{\i1}
Inserir o cálculo a que equivale:
MRS=–frac{\i1}-frac{\i}{\i1}(A,B){\i}{\i1}parcial U(A,B){\i}{\i1}(A,B){\i}
2.5 Questão Política
Determinamos no Módulo 1 que a decisão relevante do consumidor entre mais milhas percorridas e outros consumos provavelmente está de acordo com as suposições padrão sobre a escolha do consumidor. Portanto, usar a função de utilidade Cobb-Douglas para representar um consumidor que gosta de dirigir um carro, bem como de consumir outros bens, e que os vê como uma troca (dinheiro gasto em gasolina é dinheiro não gasto em outros bens de consumo), é uma boa escolha. Também tem os benefícios de estar de acordo com as suposições e ser flexível:
U(MD,C)=MD^{a}C^{\beta } ,
onde MD = Miles driven, e C = Outro consumo.
De facto, a própria função pode ser levada a dados do mundo real onde os parâmetros e pode ser estimado para este mercado, o mercado para milhas conduzido no carro do consumidor.
Gráfico de curvas de indiferença para o exemplo de política
Explorando as questões de política:
1 . Outros tipos de preferências seriam mais apropriados neste exemplo?
2. O que teria que ser verdade para que complementos perfeitos fossem o tipo de preferência apropriado para analisar esta política?
O que teria que ser verdade para substitutos perfeitos? Dado que estamos considerando um consumidor ‘típico’ que dirige, é apropriado escolher uma função de utilidade ‘típica’?
4. Estamos apenas adivinhando ou temos alguma base em teoria para suportar nossa escolha de preferências ‘bem-comportadas’ ou uma função de utilidade Cobb-Douglas?
RESUMO
Revisão: Tópicos e resultados de aprendizagem relacionados
2.1 Funções utilitárias
LO 2.1: Descrever uma função de utilidade
2.2 Funções de utilidade e preferências típicas
LO 2.2: Identificar funções de utilidade baseadas nas preferências típicas que elas representam
2.3 Relacionando Funções de Utilidade e Curvas de Indiferença Mapas
LO 2.3: Explicar como derivar uma curva de indiferença de uma função de utilidade
2.4 Encontrando Utilidade Marginal e Taxa Marginal de Substituição
LO 2.4: Derivar utilidade marginal e MRS para funções de utilidade típicas
2.5. Pergunta de política
Aprenda: Termos Chave e Gráficos
Bi-funções variáveis
Cardinal
Linha de contorno
Diminuição da utilidade marginal
>
Função
>
Marginal taxa de substituição (MRS)
>
Utilidade marginal
Ordinal
Funções univariadas
Util
Utilidade
Função de utilidade
Gráficos
3D função de utilidade e linha de contorno
Equações
Cobb-Douglas
Complementos perfeitos
Substitutos perfeitos