Nesta lição, mostraremos uma estratégia fácil para resolver o seguinte problema: como encontrar a área de um triângulo isósceles.
Ponhamos em prática algumas das propriedades que provamos até agora, no seguinte problema de geometria:
Problema
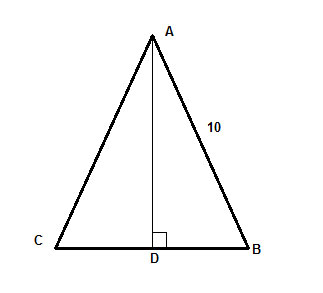
Em um triângulo isósceles, ΔABC, com comprimento de perna 10, a altura até a base é igual a dois terços da base. Encontre a área do triângulo.
Estratégia
Para resolver este problema, vamos trabalhar para trás a partir do que precisamos fazer.
Precisamos encontrar a área do triângulo que sabemos que é dada pela fórmula (base vezes altura)/2.
Um problema que temos é que não sabemos nem o comprimento da base nem a altura. Mas, nos é dada a relação entre eles, que é a dica sobre o que precisamos fazer. Vamos chamar o comprimento da base, BC, x.
Então sabemos que a altura, AD, é 2x/3, como dado no problema.
Então a resposta que estamos procurando é (base vezes altura)/2, ou x vezes 2x/3, dividido por dois.
Mas como encontramos x? Existem duas coisas adicionais que nos foram dadas no problema que ainda não utilizamos – o comprimento da perna (10), e o fato de que este é um triângulo isósceles. Provavelmente precisamos usar estas duas coisas para resolver o problema.
Vamos rever as propriedades dos triângulos isósceles. Uma coisa que deve saltar imediatamente à mente é que, como mostramos, em um triângulo isósceles, a altura para a base bissecta a base, então CD=DB=x/2.
Finalmente, AD é a altura, o que significa que o ângulo ∠ADC é um ângulo reto, e temos um triângulo direito, ΔADC, cuja hipotenusa conhecemos (10) e podemos usar para encontrar as pernas usando o teorema de Pitágoras, c2 =a2+b2,
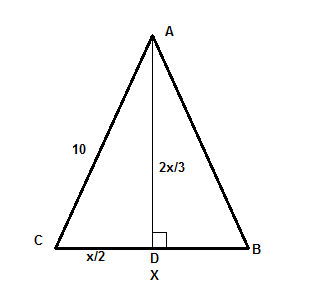
where c= 10 ,a = x/2 e b=2x/3 . E já está feito, o resto é apenas a solução algébrica para x.
Prova: área de um triângulo isósceles
(1) ΔADC é triângulo direito //g dado, como AD é a altura à base
(2) AC2 =CD2 + AD2 // Teorema de Pitágoras
(3) AC= 10 //g dado
(4) CB = x
(5) CD = x/2 //Altura à base em bissetos triangulares isósceles a base
(6) AD = 2x/3 //given
(7) 102 = (x/2)2 + (2x/3)2 //Substituir em (2)
(8) 100 = x2/4+4×2/9 //simplificar
(9) 100*36 = 9×2 +16×2 //multiplicar ambos os lados por 36
(10) 100*36 = 25×2 //colher termos semelhantes