Im modernen Audiozeitalter kommt man nicht umhin, von „Hi-Res“ und 24-Bit-Musik in „Studioqualität“ zu sprechen. Wenn Sie den Trend bei High-End-Smartphones – Sonys LDAC-Bluetooth-Codec – und Streaming-Diensten wie Tidal noch nicht bemerkt haben, dann sollten Sie wirklich anfangen, diese Seite mehr zu lesen.
Das Versprechen ist einfach – bessere Hörqualität dank mehr Daten, auch bekannt als Bittiefe. Das sind 24 Bit digitale Einsen und Nullen im Gegensatz zu den mickrigen 16 Bit aus der CD-Ära. Natürlich müssen Sie für diese höherwertigen Produkte und Dienstleistungen mehr bezahlen, aber mehr Bits sind doch sicher besser, oder?
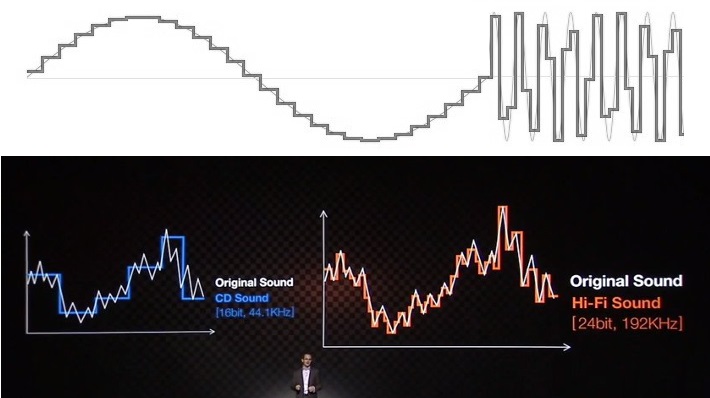
„Low-res“-Audio wird oft als treppenförmige Wellenform dargestellt. So funktioniert das Audio-Sampling nicht und so sieht es auch nicht aus, wenn Audio aus einem Gerät kommt.
Nicht unbedingt. Der Bedarf an immer höheren Bittiefen beruht nicht auf der wissenschaftlichen Realität, sondern auf einer Verdrehung der Wahrheit und dem Ausnutzen des mangelnden Bewusstseins der Verbraucher über die Wissenschaft des Klangs. Letztlich haben die Unternehmen, die 24-Bit-Audio vermarkten, weitaus mehr an Profit zu gewinnen als Sie an einer besseren Wiedergabequalität.
Bit-Tiefe und Klangqualität: Treppenstufen gibt es nicht
Um zu suggerieren, dass 24-Bit-Audio ein Muss ist, führen Unternehmen (und zu viele andere, die versuchen, dieses Thema zu erklären) die sehr bekannte Treppe zum Himmel bei der Audioqualität an. Das 16-Bit-Beispiel zeigt immer eine holprige, zerklüftete Wiedergabe einer Sinuswelle oder eines anderen Signals, während das 24-Bit-Äquivalent schön glatt und höher aufgelöst aussieht. Es ist ein einfaches visuelles Hilfsmittel, aber eines, das auf Unkenntnis des Themas und der Wissenschaft beruht, um die Verbraucher zu falschen Schlussfolgerungen zu verleiten.
Bevor mir jemand den Kopf abreißt: Technisch gesehen stellen diese Treppenbeispiele Audio im digitalen Bereich einigermaßen genau dar. Ein Stemplot/Lollipop-Diagramm ist jedoch eine genauere Grafik für die visuelle Audioabtastung als diese Treppenstufen. Ein Sample enthält eine Amplitude zu einem ganz bestimmten Zeitpunkt und nicht eine Amplitude, die über einen bestimmten Zeitraum gehalten wird.

Die Verwendung von Treppendiagrammen ist absichtlich irreführend, da Stammdiagramme eine genauere Darstellung von digitalem Audio liefern. Diese beiden Diagramme stellen die gleichen Datenpunkte dar, aber das Treppendiagramm erscheint viel ungenauer.
Es ist jedoch richtig, dass ein Analog-Digital-Wandler (ADC) ein unendliches analoges Audiosignal in eine endliche Anzahl von Bits einpassen muss. Ein Bit, das zwischen zwei Pegeln liegt, muss auf die nächstliegende Annäherung gerundet werden, was als Quantisierungsfehler oder Quantisierungsrauschen bezeichnet wird. (Merken Sie sich das, denn wir werden noch darauf zurückkommen.)
Wenn Sie sich jedoch den Audioausgang eines beliebigen Audio-Digital-Analog-Wandlers (DAC) ansehen, der in diesem Jahrhundert (und wahrscheinlich auch davor) gebaut wurde, werden Sie keine Treppenstufen entdecken. Nicht einmal, wenn Sie ein 8-Bit-Signal ausgeben. Was ist also los?

Ein 8-Bit-Sinussignal mit 10 kHz, das von einem preisgünstigen Pixel 3a-Smartphone aufgenommen wurde. Wir sehen ein gewisses Rauschen, aber keine auffälligen Treppenstufen, wie sie oft von Audiounternehmen dargestellt werden.
Erstens, was diese Treppendiagramme beschreiben, wenn wir sie auf eine Audioausgabe anwenden, ist etwas, das als Zero-Order-Hold-DAC bezeichnet wird. Dabei handelt es sich um eine sehr einfache und billige DAC-Technologie, bei der ein Signal bei jeder neuen Abtastung zwischen verschiedenen Pegeln umgeschaltet wird, um einen Ausgang zu erzeugen. Sie wird weder in professionellen noch in halbwegs vernünftigen Consumer-Audioprodukten verwendet. Man findet sie vielleicht in einem 5-Dollar-Mikrocontroller, aber sicher nirgendwo sonst. Die falsche Darstellung von Audioausgängen auf diese Weise impliziert eine verzerrte, ungenaue Wellenform, aber das ist nicht das, was Sie bekommen.

In Wirklichkeit ist ein moderner ∆Σ DAC-Ausgang ein überabgetastetes 1-Bit-PDM-Signal (rechts) und nicht ein Null-Halte-Signal (links). Letzteres erzeugt ein rauschärmeres analoges Ausgangssignal, wenn es gefiltert wird.
Audiokompatible ADCs und DACs basieren überwiegend auf Delta-Sigma-Modulation (∆Σ). Zu den Komponenten dieses Kalibers gehören Interpolation und Oversampling, Rauschformung und Filterung zur Glättung und Reduzierung von Rauschen. Delta-Sigma-DACs wandeln Audioabtastwerte in einen 1-Bit-Strom (Pulsdichtemodulation) mit einer sehr hohen Abtastrate um. Wenn dies gefiltert wird, ergibt sich ein gleichmäßiges Ausgangssignal, bei dem das Rauschen weit aus den hörbaren Frequenzen herausgedrängt wird.
Zusammenfassend lässt sich sagen, dass moderne DACs keine rau aussehenden, zerklüfteten Audiosamples ausgeben, sondern einen Bitstrom, der durch Rauschfilterung zu einem sehr genauen, gleichmäßigen Ausgangssignal wird. Diese treppenförmige Darstellung ist falsch, weil sie durch das so genannte „Quantisierungsrauschen“ verursacht wird.
Verstehen des Quantisierungsrauschens
In jedem endlichen System treten Rundungsfehler auf. Es stimmt zwar, dass ein 24-Bit-ADC oder -DAC einen geringeren Rundungsfehler hat als ein 16-Bit-Äquivalent, aber was bedeutet das eigentlich? Und was noch wichtiger ist: Was hören wir eigentlich? Ist es Verzerrung oder Fuzz, gehen Details für immer verloren?
Eigentlich ist es ein bisschen von beidem, je nachdem, ob man sich im digitalen oder analogen Bereich bewegt. Das Schlüsselkonzept, um beides zu verstehen, ist der Umgang mit dem Grundrauschen und wie sich dieses mit zunehmender Bit-Tiefe verbessert. Zur Veranschaulichung gehen wir von 16 und 24 Bit aus und betrachten Beispiele mit sehr geringer Bittiefe.
Der Unterschied zwischen 16 und 24 Bittiefen ist nicht die Genauigkeit in der Form einer Wellenform, sondern die verfügbare Grenze, bevor digitales Rauschen unser Signal stört.
Im folgenden Beispiel gibt es eine ganze Reihe von Dingen zu überprüfen, daher zunächst eine kurze Erklärung, was wir betrachten. In den oberen Diagrammen sehen wir unsere Eingangs- (blau) und quantisierten (orange) Wellenformen mit einer Bittiefe von 2, 4 und 8 Bit. Wir haben unserem Signal auch eine kleine Menge Rauschen hinzugefügt, um die reale Welt besser zu simulieren. Unten sehen Sie ein Diagramm des Quantisierungsfehlers oder Rundungsrauschens, das berechnet wird, indem das quantisierte Signal vom Eingangssignal subtrahiert wird.

Das Quantisierungsrauschen nimmt aufgrund von Rundungsfehlern zu, je kleiner die Bittiefe ist.
Durch die Erhöhung der Bittiefe wird das quantisierte Signal eindeutig besser an das Eingangssignal angepasst. Das ist aber nicht das Entscheidende, man beachte das viel größere Fehler-/Rauschsignal bei den niedrigeren Bittiefen. Das quantisierte Signal hat keine Daten aus dem Eingangssignal entfernt, sondern das Fehlersignal hinzugefügt. Die additive Synthese besagt, dass ein Signal durch die Summe von zwei beliebigen anderen Signalen reproduziert werden kann, einschließlich phasenverschobener Signale, die als Subtraktion wirken. So funktioniert auch die Rauschunterdrückung. Diese Rundungsfehler führen also ein neues Rauschsignal ein.
Dies ist nicht nur theoretisch, man kann tatsächlich immer mehr Rauschen in Audiodateien mit geringerer Bit-Tiefe hören. Um zu verstehen, warum das so ist, schauen Sie sich an, was in dem 2-Bit-Beispiel mit sehr kleinen Signalen passiert, z. B. vor 0,2 Sekunden. Klicken Sie hier für eine vergrößerte Grafik. Sehr kleine Änderungen im Eingangssignal führen zu großen Änderungen in der quantisierten Version. Dies ist der Rundungsfehler, der dazu führt, dass das Rauschen kleiner Signale verstärkt wird. Auch hier wird das Rauschen lauter, wenn die Bittiefe abnimmt.
Durch die Quantisierung werden keine Daten aus dem Eingangssignal entfernt, sondern es wird ein verrauschtes Fehlersignal hinzugefügt.
Denken Sie dies auch umgekehrt: Es ist nicht möglich, ein Signal zu erfassen, das kleiner ist als die Größe des Quantisierungsschritts – ironischerweise als das niedrigstwertige Bit bekannt. Kleine Signaländerungen müssen auf die nächsthöhere Quantisierungsstufe springen. Größere Bittiefen haben kleinere Quantisierungsschritte und damit eine geringere Rauschverstärkung.
Am wichtigsten ist jedoch, dass die Amplitude des Quantisierungsrauschens unabhängig von der Amplitude der Eingangssignale gleich bleibt. Dies zeigt, dass das Rauschen auf allen verschiedenen Quantisierungsebenen auftritt, so dass bei jeder Bittiefe ein gleichmäßiger Rauschpegel vorhanden ist. Größere Bit-Tiefen erzeugen weniger Rauschen. Wir sollten daher die Unterschiede zwischen 16 und 24 Bittiefen nicht als die Genauigkeit in der Form einer Wellenform betrachten, sondern als die verfügbare Grenze, bevor digitales Rauschen unser Signal stört.
Bit-Tiefe hat mit Rauschen zu tun
Nun, da wir über Bit-Tiefe in Bezug auf Rauschen sprechen, lassen Sie uns ein letztes Mal zu unseren obigen Grafiken zurückkehren. Beachten Sie, dass das 8-Bit-Beispiel eine fast perfekte Übereinstimmung mit unserem verrauschten Eingangssignal darstellt. Das liegt daran, dass die 8-Bit-Auflösung tatsächlich ausreicht, um den Pegel des Hintergrundrauschens zu erfassen. Mit anderen Worten: Die Quantisierungsschrittweite ist kleiner als die Amplitude des Rauschens, oder das Signal-Rausch-Verhältnis (SNR) ist besser als der Pegel des Hintergrundrauschens.
Die Gleichung 20log(2n), wobei n die Bittiefe ist, liefert uns das SNR. Ein 8-Bit-Signal hat einen SNR von 48 dB, ein 12-Bit-Signal von 72 dB, ein 16-Bit-Signal von 96 dB und ein 24-Bit-Signal von satten 144 dB. Dies ist wichtig, da wir jetzt wissen, dass wir nur eine Bittiefe mit einem SNR benötigen, der den Dynamikbereich zwischen unserem Hintergrundrauschen und dem lautesten Signal, das wir aufnehmen wollen, abdeckt, um Audio so perfekt wie in der realen Welt wiederzugeben. Es wird ein wenig schwierig, von den relativen Maßstäben der digitalen Welt zu den schalldruckbasierten Maßstäben der physischen Welt überzugehen, also versuchen wir, es einfach zu halten.
Wir benötigen eine Bittiefe mit genügend SNR, um unser Hintergrundrauschen zu berücksichtigen, damit unser Audio so perfekt wie in der realen Welt klingt.
Ihr Ohr hat eine Empfindlichkeit von 0 dB (Stille) bis etwa 120 dB (schmerzhaft lauter Ton), und die typische Fähigkeit, Lautstärken zu unterscheiden, liegt nur 1 dB auseinander. Der dynamische Bereich deines Ohrs beträgt also etwa 120 dB, also fast 20 Bit.
Doch du kannst nicht alles auf einmal hören, da sich das Trommelfell zusammenzieht, um die Lautstärke, die das Innenohr in lauten Umgebungen erreicht, zu verringern. Sie werden auch keine Musik hören, die auch nur annähernd so laut ist, weil Sie sonst taub werden. Außerdem sind die Umgebungen, in denen Sie und ich Musik hören, nicht so leise, wie es gesunde Ohren hören können. In einem gut ausgestatteten Aufnahmestudio können wir die Hintergrundgeräusche auf unter 20 dB senken, aber das Hören in einem belebten Wohnzimmer oder im Bus verschlechtert natürlich die Bedingungen und verringert unseren Bedarf an einem hohen Dynamikbereich.
Das menschliche Ohr hat einen riesigen Dynamikbereich, aber eben nicht alles auf einmal. Maskierung und Gehörschutz vermindern seine Wirksamkeit.
Hinzu kommt: Mit zunehmender Lautstärke wirkt die Maskierung höherer Frequenzen im Ohr. Bei niedrigen Lautstärken von 20 bis 40 dB tritt keine Maskierung auf, es sei denn, es handelt sich um Geräusche mit geringer Tonhöhe. Bei 80 dB werden jedoch Geräusche unter 40 dB maskiert, während bei 100 dB Geräusche unter 70 dB nicht mehr hörbar sind. Aufgrund der Dynamik des Ohres und des Hörmaterials ist es schwierig, eine genaue Zahl zu nennen, aber der tatsächliche Dynamikbereich Ihres Gehörs liegt wahrscheinlich im Bereich von 70 dB in einer durchschnittlichen Umgebung, bis hinunter zu nur 40 dB in sehr lauten Umgebungen. Eine Bittiefe von nur 12 Bit würde wahrscheinlich für die meisten Menschen ausreichen, so dass 16-Bit-CDs viel Spielraum bieten.

hyperphysics Bei hohen Lautstärken kommt es zu einer hochfrequenten Maskierung, die unsere Wahrnehmung von leiseren Klängen einschränkt.
Die meisten Instrumente und Aufnahmemikrofone verursachen auch Rauschen (insbesondere Gitarrenverstärker), selbst in sehr leisen Aufnahmestudios. Es gibt auch einige Studien über den Dynamikbereich verschiedener Genres, darunter diese, die einen typischen Dynamikbereich von 60 dB zeigt. Es überrascht nicht, dass Genres mit einer größeren Affinität zu leisen Teilen, wie Chor, Oper und Klavier, maximale Dynamikbereiche um 70 dB aufweisen, während „lautere“ Rock-, Pop- und Rap-Genres eher zu 60 dB und darunter tendieren. Letztlich wird Musik nur mit einer bestimmten Lautstärke produziert und aufgenommen.
Sie kennen vielleicht auch die „Loudness Wars“ der Musikindustrie, die den Zweck der heutigen Hi-Res-Audioformate mit Sicherheit zunichte machen. Starke Kompression (die Rauschen verstärkt und Spitzen abschwächt) reduziert den Dynamikbereich. Moderne Musik hat einen wesentlich geringeren Dynamikbereich als Alben von vor 30 Jahren. Theoretisch könnte moderne Musik mit niedrigeren Bitraten verbreitet werden als alte Musik. Hier können Sie den Dynamikbereich einer Reihe von Alben überprüfen.

CD-Qualität mag „nur“ 16-Bit sein, aber das ist ein Overkill für die Qualität.
16 Bit ist alles, was Sie brauchen
Das war eine ganz schöne Reise, aber ich hoffe, Sie haben ein viel nuancierteres Bild von Bittiefe, Rauschen und Dynamikbereich erhalten als diese irreführenden Treppenbeispiele, die Sie so oft sehen.
Bit-Tiefe hat mit Rauschen zu tun, und je mehr Datenbits Sie zum Speichern von Audiodaten haben, desto weniger Quantisierungsrauschen wird in Ihre Aufnahme eingebracht. Aus demselben Grund können Sie auch kleinere Signale genauer erfassen, was dazu beiträgt, das digitale Grundrauschen unter die Aufnahme- oder Hörumgebung zu drücken. Das ist alles, wozu wir die Bittiefe brauchen. Es gibt keinen Vorteil, große Bittiefen für Audio-Master zu verwenden.
Überraschenderweise sind 12 Bit wahrscheinlich genug für ein anständig klingendes Musik-Master und um den dynamischen Bereich der meisten Hörumgebungen abzudecken. Digitales Audio transportiert jedoch mehr als nur Musik, und Beispiele wie Sprach- oder Umgebungsaufnahmen für das Fernsehen können einen größeren Dynamikbereich nutzen als die meisten Musikstücke. Und ein wenig Spielraum für die Trennung zwischen laut und leise hat noch niemandem geschadet.
Im Großen und Ganzen wird mit 16 Bit (96 dB Dynamikbereich oder 120 dB mit Dithering) eine breite Palette von Audiotypen sowie die Grenzen des menschlichen Gehörs und typische Hörumgebungen abgedeckt. Die wahrnehmbare Verbesserung der 24-Bit-Qualität ist höchst fragwürdig, wenn nicht sogar ein Placebo, wie ich hoffentlich gezeigt habe. Außerdem sind sie durch die Zunahme der Dateigrößen und der Bandbreite unnötig. Die Art der Komprimierung, die verwendet wird, um die Dateigröße Ihrer Musikbibliothek oder Ihres Streams zu verringern, hat einen viel stärkeren Einfluss auf die Klangqualität als die Frage, ob es sich um eine 16- oder 24-Bit-Datei handelt.