Die Standardabweichung ist die durchschnittliche Schwankungsbreite in Ihrem Datensatz. Sie gibt an, wie weit jeder Wert im Durchschnitt vom Mittelwert entfernt ist.
Eine hohe Standardabweichung bedeutet, dass die Werte im Allgemeinen weit vom Mittelwert entfernt sind, während eine niedrige Standardabweichung darauf hinweist, dass die Werte nahe am Mittelwert liegen.
Was sagt die Standardabweichung aus?
Die Standardabweichung ist ein nützliches Maß für die Streuung von Normalverteilungen.
Bei Normalverteilungen sind die Daten symmetrisch und nicht schief verteilt. Die meisten Werte gruppieren sich um einen zentralen Bereich, wobei sich die Werte mit zunehmender Entfernung vom Zentrum verjüngen. Die Standardabweichung gibt an, wie weit die Daten im Durchschnitt von der Mitte der Verteilung entfernt sind.
Viele wissenschaftliche Variablen folgen Normalverteilungen, einschließlich Körpergröße, standardisierte Testergebnisse oder Bewertungen der Arbeitszufriedenheit. Wenn Sie die Standardabweichungen verschiedener Stichproben haben, können Sie deren Verteilungen mithilfe statistischer Tests vergleichen, um Rückschlüsse auf die größeren Populationen zu ziehen, aus denen sie stammen.
Der Mittelwert (M) der Bewertungen ist für jede Gruppe gleich – das ist der Wert auf der x-Achse, wenn die Kurve ihren Höhepunkt erreicht. Ihre Standardabweichungen (SD) unterscheiden sich jedoch voneinander.
Die Standardabweichung spiegelt die Streuung der Verteilung wider. Die Kurve mit der niedrigsten Standardabweichung hat eine hohe Spitze und eine geringe Streuung, während die Kurve mit der höchsten Standardabweichung flacher und breiter ist.
Die empirische Regel
Die Standardabweichung und der Mittelwert zusammen können Ihnen sagen, wo die meisten Werte in Ihrer Verteilung liegen, wenn sie einer Normalverteilung folgen.
Die empirische Regel oder die 68-95-99,7-Regel sagt Ihnen, wo Ihre Werte liegen:
- Rund 68% der Ergebnisse liegen innerhalb von 2 Standardabweichungen vom Mittelwert,
- Rund 95% der Ergebnisse liegen innerhalb von 4 Standardabweichungen vom Mittelwert,
- Rund 99.7% der Ergebnisse liegen innerhalb von 6 Standardabweichungen vom Mittelwert.
Die empirische Regel lautet:
- Rund 68% der Ergebnisse liegen zwischen 40 und 60.
- Rund 95% der Ergebnisse liegen zwischen 30 und 70.
- Rund 99,7 % der Werte liegen zwischen 20 und 80.
Die empirische Regel ist eine schnelle Möglichkeit, sich einen Überblick über Ihre Daten zu verschaffen und zu prüfen, ob es Ausreißer oder Extremwerte gibt, die nicht diesem Muster folgen.
Bei Nicht-Normalverteilungen ist die Standardabweichung ein weniger zuverlässiges Maß für die Variabilität und sollte in Kombination mit anderen Maßen wie dem Bereich oder dem Interquartilsbereich verwendet werden.
Standardabweichungsformeln für Grundgesamtheiten und Stichproben
Abhängig davon, ob Sie Daten aus einer Grundgesamtheit oder einer Stichprobe haben, werden unterschiedliche Formeln zur Berechnung der Standardabweichungen verwendet.
Standardabweichung der Grundgesamtheit
Wenn Sie Daten von allen Mitgliedern der Grundgesamtheit gesammelt haben, die Sie interessieren, können Sie einen genauen Wert für die Standardabweichung der Grundgesamtheit erhalten.
Die Formel für die Standardabweichung der Bevölkerung sieht wie folgt aus:
| Formel | Erläuterung |
|---|---|
 |
|
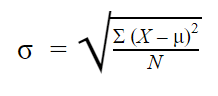Stichprobenstandardabweichung
Wenn man Daten aus einer Stichprobe erhebt, wird die Stichprobenstandardabweichung verwendet, um Schätzungen oder Rückschlüsse auf die Standardabweichung der Grundgesamtheit zu ziehen.
Die Formel für die Stichprobenstandardabweichung sieht wie folgt aus:
| Formel | Erläuterung |
|---|---|
 |
|
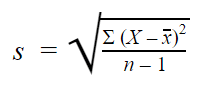Bei Stichproben verwenden wir n – 1 in der Formel, da die Verwendung von n zu einer verzerrten Schätzung führen würde, die die Variabilität durchweg unterschätzt. Die Standardabweichung der Stichprobe wäre tendenziell niedriger als die tatsächliche Standardabweichung der Grundgesamtheit.
Wenn man die Stichprobe von n auf n – 1 reduziert, wird die Standardabweichung künstlich groß und man erhält eine konservative Schätzung der Variabilität.
Dies ist zwar keine unverzerrte Schätzung, aber eine weniger verzerrte Schätzung der Standardabweichung: Es ist besser, die Variabilität in Stichproben zu überschätzen als zu unterschätzen.
Schritte zur Berechnung der Standardabweichung
Die Standardabweichung wird normalerweise automatisch von der Software berechnet, die Sie für Ihre statistische Analyse verwenden. Sie können sie aber auch von Hand berechnen, um besser zu verstehen, wie die Formel funktioniert.
Es gibt sechs Hauptschritte, um die Standardabweichung von Hand zu ermitteln. Wir verwenden einen kleinen Datensatz mit 6 Werten, um die Schritte zu erläutern.
| Datensatz | |||||
|---|---|---|---|---|---|
| 46 | 69 | 32 | 60 | 52 | 41 |
Schritt 1: Finde den Mittelwert
Um den Mittelwert zu finden, addiere alle Punkte und teile sie dann durch die Anzahl der Punkte.
x̅ = (46 + 69 + 32 + 60 + 52 + 41) ÷ 6 = 50
Schritt 2: Finde die Abweichung jeder Punktzahl vom Mittelwert
Subtrahiere den Mittelwert von jeder Punktzahl, um die Abweichungen vom Mittelwert zu erhalten.
Da x̅ = 50 ist, ziehen wir hier von jeder Punktzahl 50 ab.
| Punktzahl | Abweichung vom Mittelwert |
|---|---|
| 46 | 46 – 50 = -4 |
| 69 | 69 – 50 = 19 |
| 32 | 32 – 50 = -18 |
| 60 | 60 – 50 = 10 |
| 52 | 52 – 50 = 2 |
| 41 | 41 – 50 = -9 |
Schritt 3: Quadriere jede Abweichung vom Mittelwert
Multipliziere jede Abweichung vom Mittelwert mit sich selbst. Das Ergebnis sind positive Zahlen.
(-4)2 = 4 × 4 = 16
192 = 19 × 19 = 361
(-18)2 = -18 × -18 = 324
102 = 10 × 10 = 100
22 = 2 × 2 = 4
(-9)2 = -9 × -9 = 81
Schritt 4: Finde die Summe der Quadrate
Addiere alle quadrierten Abweichungen zusammen. Dies nennt man die Summe der Quadrate.
16 + 361 + 324 + 100 + 4 + 81 = 886
Schritt 5: Finde die Varianz
Dividiere die Summe der Quadrate durch n – 1 (für eine Stichprobe) oder N (für eine Grundgesamtheit) – dies ist die Varianz.
Da wir mit einem Stichprobenumfang von 6 arbeiten, verwenden wir n – 1, wobei n = 6 ist.
886 ÷ (6 – 1) = 886 ÷ 5 = 177.2
Schritt 6: Finde die Quadratwurzel der Varianz
Um die Standardabweichung zu finden, nehmen wir die Quadratwurzel der Varianz.
√177.2 = 13.31
Aus der Erkenntnis, dass SD = 13.31 ist, können wir sagen, dass jede Punktzahl im Durchschnitt um 13,31 Punkte vom Mittelwert abweicht.
Warum ist die Standardabweichung ein nützliches Maß für die Variabilität?
Obwohl es einfachere Methoden zur Berechnung der Variabilität gibt, gewichtet die Formel für die Standardabweichung ungleichmäßig verteilte Stichproben stärker als gleichmäßig verteilte Stichproben. Eine höhere Standardabweichung besagt, dass die Verteilung nicht nur stärker, sondern auch ungleichmäßiger verteilt ist.
Das bedeutet, dass sie Ihnen eine bessere Vorstellung von der Variabilität Ihrer Daten vermittelt als einfachere Maße wie die mittlere absolute Abweichung (MAD).
Die MAD ist der Standardabweichung ähnlich, aber einfacher zu berechnen. Zunächst drückt man jede Abweichung vom Mittelwert in absoluten Werten aus, indem man sie in positive Zahlen umwandelt (z. B. wird aus -3 eine 3). Dann berechnet man den Mittelwert dieser absoluten Abweichungen.
Im Gegensatz zur Standardabweichung muss man bei der MAD keine Quadrate oder Quadratwurzeln von Zahlen berechnen. Aus diesem Grund liefert sie jedoch ein weniger präzises Maß für die Variabilität.
Nehmen wir zwei Stichproben mit der gleichen zentralen Tendenz, aber unterschiedlich großer Variabilität. Die Stichprobe B ist variabler als die Stichprobe A.
| Werte | Mittelwert | mittlere absolute Abweichung | Standardabweichung | |
|---|---|---|---|---|
| Probe A | 66, 30, 40, 64 | 50 | 15 | 17.8 |
| Stichprobe B | 51, 21, 79, 49 | 50 | 15 | 23,7 |
Bei Stichproben mit gleichen durchschnittlichen Abweichungen vom Mittelwert kann die MAD keine Unterscheidung der Streuungsgrade vornehmen. Die Standardabweichung ist präziser: Sie ist höher für die Stichprobe mit größeren Abweichungen vom Mittelwert.
Durch die Quadrierung der Abweichungen vom Mittelwert spiegelt die Standardabweichung die ungleichmäßige Streuung genauer wider. Bei diesem Schritt werden extreme Abweichungen stärker gewichtet als kleine Abweichungen.
Dies macht die Standardabweichung jedoch auch empfindlich gegenüber Ausreißern.
Häufig gestellte Fragen zur Standardabweichung
Variabilität wird am häufigsten mit den folgenden deskriptiven Statistiken gemessen:
- Bereich: die Differenz zwischen dem höchsten und dem niedrigsten Wert
- Interquartilsbereich: Bereich der mittleren Hälfte einer Verteilung
- Standardabweichung: durchschnittlicher Abstand vom Mittelwert
- Varianz: Durchschnitt der quadrierten Abstände vom Mittelwert
Die Standardabweichung ist der durchschnittliche Wert der Variabilität in Ihrem Datensatz. Sie gibt an, wie weit die einzelnen Werte im Durchschnitt vom Mittelwert entfernt sind.
In Normalverteilungen bedeutet eine hohe Standardabweichung, dass die Werte im Allgemeinen weit vom Mittelwert entfernt sind, während eine niedrige Standardabweichung anzeigt, dass die Werte nahe am Mittelwert liegen.
Bei einer Normalverteilung sind die Daten symmetrisch und nicht schief verteilt. Die meisten Werte gruppieren sich um einen zentralen Bereich, wobei sich die Werte verjüngen, je weiter sie sich vom Zentrum entfernen.
Die Maße der zentralen Tendenz (Mittelwert, Modus und Median) sind in einer Normalverteilung genau gleich.
Die empirische Regel oder die 68-95-99,7-Regel gibt an, wo die meisten Werte in einer Normalverteilung liegen:
- Rund 68% der Werte liegen innerhalb von 1 Standardabweichung vom Mittelwert.
- Rund 95% der Werte liegen innerhalb von 2 Standardabweichungen vom Mittelwert.
- Rund 99.7% der Werte liegen innerhalb von 3 Standardabweichungen vom Mittelwert.
Die empirische Regel ist eine schnelle Möglichkeit, sich einen Überblick über die Daten zu verschaffen und nach Ausreißern oder Extremwerten zu suchen, die nicht diesem Muster folgen.
Die Varianz ist die durchschnittliche quadratische Abweichung vom Mittelwert, während die Standardabweichung die Quadratwurzel aus dieser Zahl ist. Beide Maße spiegeln die Variabilität in einer Verteilung wider, aber ihre Einheiten unterscheiden sich:
- Die Standardabweichung wird in denselben Einheiten wie die ursprünglichen Werte ausgedrückt (z. B. Minuten oder Meter).
- Die Varianz wird in viel größeren Einheiten ausgedrückt (z. B. Meter zum Quadrat).
Obwohl die Einheiten der Varianz intuitiv schwerer zu verstehen sind, ist die Varianz bei statistischen Tests wichtig.