Proton

Zerfall des Neutrons

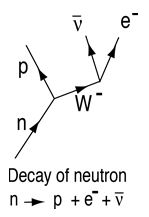
Ein freies Neutron zerfällt mit einer Halbwertszeit von etwa 10,3 Minuten, aber es ist stabil, wenn es sich mit einem Kern verbindet. Dieser Zerfall ist ein Beispiel für einen Betazerfall mit der Emission eines Elektrons und eines Elektronen-Antineutrinos. Der Zerfall des Neutrons beruht auf der schwachen Wechselwirkung, wie im Feynman-Diagramm rechts dargestellt.

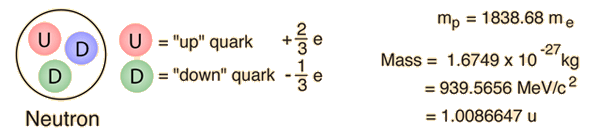
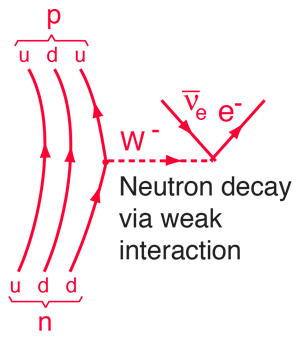Ein detaillierteres Diagramm des Neutronenzerfalls zeigt, dass es sich um die Umwandlung eines der Down-Quarks des Neutrons in ein Up-Quark handelt. Dies ist ein Beispiel für die Art von Quarkumwandlungen, die an vielen Kernprozessen beteiligt sind, einschließlich des Betazerfalls.

Der Zerfall des Neutrons ist ein gutes Beispiel für die Beobachtungen, die zur Entdeckung des Neutrinos führten. Eine Analyse der Energetik des Zerfalls kann zur Veranschaulichung der Dilemmata dienen, mit denen die frühen Forscher dieses Prozesses konfrontiert waren.

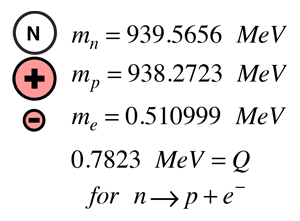Wenn man das Konzept der Bindungsenergie verwendet und die Massen der Teilchen durch ihre Ruhemassenenergien darstellt, kann die Energieausbeute des Neutronenzerfalls aus den Teilchenmassen berechnet werden. Die Energieausbeute wird traditionell durch das Symbol Q dargestellt. Da Energie und Impuls beim Zerfall erhalten bleiben müssen, wird gezeigt, dass das leichtere Elektron den größten Teil der kinetischen Energie mitnimmt. Bei einer kinetischen Energie dieser Größenordnung muss der relativistische Ausdruck für die kinetische Energie verwendet werden.

Für den Moment nehmen wir (fälschlicherweise) an, dass der Zerfall nur das Proton und das Elektron als Produkte umfasst. Die Energieausbeute Q würde dann zwischen dem Proton und dem Elektron aufgeteilt werden. Das Elektron erhält den größten Teil der kinetischen Energie und ist relativistisch, das Proton hingegen ist nicht relativistisch. Die Energiebilanz ist dann

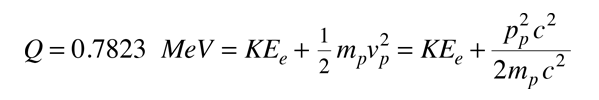
im Ruhezustand des Neutrons, erfordert die Impulserhaltung

Pelektron = – pcproton

und pcelectron kann in Form der kinetischen Energie des Elektrons ausgedrückt werden

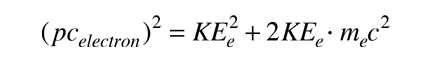Anzeigen

Die Energiebilanz lautet dann

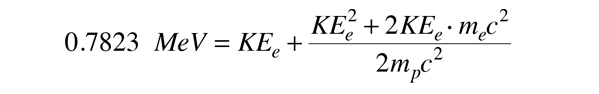
Wenn man die Zahlen für diesen Wert von Q ersetzt, sieht man, dass der Term KEe2 vernachlässigbar ist, so dass die erforderliche kinetische Energie des Elektrons berechnet werden kann. Die erforderliche kinetische Energie des Elektrons für dieses Zwei-Teilchen-Zerfallsschema ist

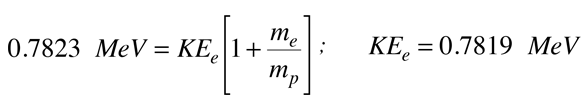
Auch der Impuls des Elektrons für diesen Zwei-Teilchen-Zerfall muss

Der Impuls und die Energie für den Zwei-Teilchen-Zerfall sind auf diese Werte beschränkt, aber das ist nicht das Verhalten der Natur. Die beobachteten Impuls- und Energieverteilungen für das Elektron sind wie unten dargestellt.

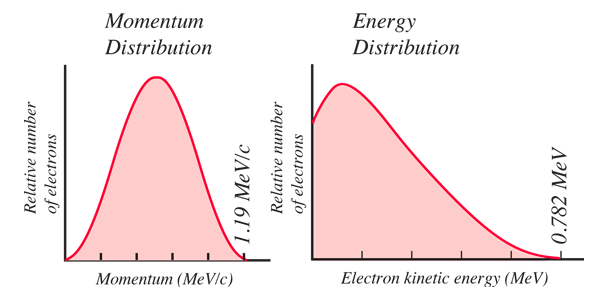
Die Tatsache, dass die beim Neutronenzerfall erzeugten Elektronen kontinuierliche Energie- und Impulsverteilungen aufwiesen, war ein klarer Hinweis darauf, dass neben dem Elektron und dem Proton ein weiteres Teilchen emittiert wurde. Es musste ein neutrales Teilchen sein und trug bei bestimmten Zerfällen fast die gesamte Energie und den gesamten Impuls des Zerfalls. Dies wäre nicht so außergewöhnlich, wenn nicht das Elektron mit seiner maximalen Bewegungsenergie die gesamte für den Zerfall verfügbare Energie Q auf sich vereinigt hätte. Es blieb also keine Energie übrig, um die Massenenergie des anderen emittierten Teilchens zu berücksichtigen. Die frühen Experimentatoren standen vor dem Dilemma eines Teilchens, das fast die gesamte Energie und den Impuls des Zerfalls tragen konnte, aber keine Ladung und anscheinend auch keine Masse hatte!

Das mysteriöse Teilchen wurde Neutrino genannt, aber es dauerte fünfundzwanzig Jahre, bis Cowan und Reines das Neutrino eindeutig experimentell beobachteten. Das heutige Verständnis des Neutronenzerfalls ist

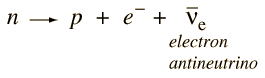
Dieser Zerfall veranschaulicht einige der Erhaltungssätze, die für Teilchenzerfälle gelten. Das Proton im Produkt erfüllt die Erhaltung der Baryonenzahl, aber das unbegleitete Auftauchen des Elektrons würde die Erhaltung der Leptonenzahl verletzen. Das dritte Teilchen muss ein Elektron-Antineutrino sein, damit der Zerfall der Leptonenzahlerhaltung entspricht. Das Elektron hat die Leptonenzahl 1 und das Antineutrino hat die Leptonenzahl -1.

Experimenteller Nachweis von Neutrinos

Stabilität des Neutrons im Deuteron