
Die politische Frage: Steuergutschrift für den Kauf von Hybridautos – ist sie die beste Wahl der Regierung, um den Kraftstoffverbrauch und die Kohlenstoffemissionen zu reduzieren?
Die US-Bürger und die Regierung sind besorgt über die Abhängigkeit von importiertem ausländischem Öl und die Freisetzung von Kohlenstoff in die Atmosphäre. Im Jahr 2005 verabschiedete der Kongress ein Gesetz, das den Verbrauchern Steuergutschriften für den Kauf von Elektro- und Hybridautos gewährt.
Diese Steuergutschriften scheinen eine gute politische Entscheidung zu sein, aber sie sind kostspielig, da sie die Einnahmen der US-Regierung direkt verringern. Gibt es wirksamere Ansätze zur Verringerung der Abhängigkeit von fossilen Brennstoffen und Kohlenstoffemissionen? Wie können wir entscheiden, welche Politik die beste ist? Um diese Frage zu beantworten, müssen die politischen Entscheidungsträger mit einiger Genauigkeit vorhersagen, wie die Verbraucher auf diese Steuerpolitik reagieren werden, bevor sie Millionen von Bundesdollar ausgeben.
Wir können das Konzept des Nutzens auf diese politische Frage anwenden. In diesem Modul werden wir Nutzen und Nutzenfunktionen untersuchen. Wir werden dann in der Lage sein, eine geeignete Nutzenfunktion zu verwenden, um Indifferenzkurven abzuleiten, die unsere politische Frage beschreiben.
Untersuchung der politischen Frage
Angenommen, die Steuergutschrift zur Subventionierung des Kaufs von Hybridautos ist sehr erfolgreich und verdoppelt den durchschnittlichen Kraftstoffverbrauch aller Autos auf den Straßen der USA – ein Ergebnis, das natürlich nicht realistisch ist, aber für unsere späteren Diskussionen nützlich ist. Was glauben Sie, was mit dem Kraftstoffverbrauch aller Autofahrer in den USA passieren würde? Sollte die Regierung erwarten, dass der Kraftstoffverbrauch und die Kohlendioxidemissionen von Autos daraufhin um die Hälfte zurückgehen? Warum oder warum nicht?
2.1 Nutzenfunktionen
LO 2.1: Beschreiben Sie eine Nutzenfunktion.
2.2 Nutzenfunktionen und typische Präferenzen
LO 2.2: Identifizieren Sie Nutzenfunktionen anhand der typischen Präferenzen, die sie repräsentieren.
2.3 Setzen Sie Nutzenfunktionen und Indifferenzkurven in Beziehung.
LO 2.3: Erklären Sie, wie man eine Indifferenzkurve aus einer Nutzenfunktion ableitet.
2.4 Finden Sie Grenznutzen und marginale Substitutionsrate
LO 2.4: Leiten Sie Grenznutzen und MRS für typische Nutzenfunktionen ab.
2.5. Politische Fragestellung
2.1 Nutzenfunktionen
LO1: Beschreiben Sie eine Nutzenfunktion.
Unsere Präferenzen erlauben es uns, Vergleiche zwischen verschiedenen Konsumbündeln anzustellen und die bevorzugten Bündel zu wählen. Wir können z. B. die Rangfolge einer ganzen Reihe von Bündeln auf der Grundlage unserer Präferenzen bestimmen. Eine Nutzenfunktion ist eine mathematische Funktion, die Bündel von Konsumgütern in eine Rangfolge bringt, indem sie jedem Bündel eine Zahl zuweist, wobei größere Zahlen bevorzugte Bündel anzeigen. Nutzenfunktionen haben die Eigenschaften, die wir in Modul 1 in Bezug auf Präferenzen festgestellt haben. Das heißt: Sie sind in der Lage, Bündel zu ordnen, sie sind vollständig und transitiv, mehr wird gegenüber weniger bevorzugt und in relevanten Fällen sind gemischte Bündel besser.
Die Zahl, die die Nutzenfunktion einem bestimmten Bündel zuordnet, wird als Nutzen bezeichnet, die Zufriedenheit, die ein Verbraucher mit einem bestimmten Bündel hat. Die Nutzenzahl für jedes Bündel hat keine absolute Bedeutung; es gibt keinen einheitlichen Maßstab, an dem wir die Zufriedenheit messen. Er hat nur eine relative Bedeutung: Mit Hilfe des Nutzens lässt sich bestimmen, welche Bündel anderen vorgezogen werden.
Ist der Nutzen von Bündel A höher als der von Bündel B, so bedeutet dies, dass ein Verbraucher Bündel A gegenüber Bündel B bevorzugt. Nutzwertfunktionen ordnen daher die Präferenzen der Verbraucher ein, indem sie jedem Bündel eine Zahl zuweisen. . Wir können eine Nutzenfunktion verwenden, um die in Modul 1 beschriebenen Indifferenzkurvenkarten zu zeichnen. Da alle Bündel auf derselben Indifferenzkurve die gleiche Zufriedenheit bieten und daher keines bevorzugt wird, hat jedes Bündel den gleichen Nutzen. Wir können daher eine Indifferenzkurve zeichnen, indem wir alle Bündel bestimmen, die die gleiche Zahl aus der Nutzenfunktion ergeben.
Ökonomen sagen, dass Nutzenfunktionen ordinal und nicht kardinal sind. Ordinal bedeutet, dass Nutzenfunktionen lediglich eine Rangfolge der Bündel aufstellen – sie geben nur an, welches Bündel besser ist, nicht aber, wie viel besser es im Vergleich zu einem anderen Bündel ist. Nehmen wir zum Beispiel an, dass eine Nutzenfunktion angibt, dass Bündel A 10 Nutzen bringt und Bündel B 20 Nutzen. Wir sagen nicht, dass Bündel B doppelt so gut oder 10 Nutzen besser ist, sondern nur, dass der Verbraucher Bündel B bevorzugt. Angenommen, eine Freundin nimmt an einem Rennen teil und erzählt Ihnen, dass sie den dritten Platz belegt hat. Diese Information ist ordinal: Sie wissen, dass sie schneller war als der viertplatzierte Läufer und langsamer als der zweitplatzierte Läufer. Sie kennen nur die Reihenfolge, in der die Läufer ins Ziel kamen. Die einzelnen Zeiten sind kardinal: Wenn der Erstplatzierte das Rennen in genau einer Stunde gelaufen ist und Ihr Freund in einer Stunde und sechs Minuten, wissen Sie, dass Ihr Freund genau 10 % langsamer war als der schnellste Läufer. Da Nutzenfunktionen ordinal sind, können viele verschiedene Nutzenfunktionen dieselben Präferenzen darstellen. Dies gilt, solange die Reihenfolge beibehalten wird.
Nehmen wir zum Beispiel die Nutzenfunktion U, die Präferenzen über Güterbündel A und B beschreibt: U(A,B). Wir können eine beliebige positive monotone Transformation auf diese Funktion anwenden (was im Wesentlichen bedeutet, dass wir die Reihenfolge nicht ändern) und die neue Funktion, die wir geschaffen haben, wird dieselben Präferenzen darstellen. Zum Beispiel könnten wir eine positive Konstante α multiplizieren oder eine positive oder negative Konstante β hinzufügen. So repräsentiert αU(A,B)+β genau dieselben Präferenzen wie U(A,B), weil es die Bündel auf genau dieselbe Weise ordnet. Diese Tatsache ist recht nützlich, denn manchmal erleichtert die Anwendung einer positiven monotonen Transformation einer Nutzenfunktion die Lösung von Problemen.
2.2 Nutzenfunktionen und typische Präferenzen
LO2: Identifizieren Sie Nutzenfunktionen anhand der typischen Präferenzen, die sie darstellen
Betrachten Sie Bündel von Äpfeln, A, und Bananen, B. Eine Nutzenfunktion, die Isaacs Präferenzen für Bündel von Äpfeln und Bananen beschreibt, ist die Funktion U(A,B). Aber was sind Isaacs besondere Präferenzen für Bündel von Äpfeln und Bananen? Nehmen wir an, dass Isaac ziemlich normale Präferenzen für Äpfel und Bananen hat, die zu unseren typischen Indifferenzkurven führen: Er bevorzugt mehr gegenüber weniger, und er mag Vielfalt. Eine Nutzenfunktion, die diese Präferenzen repräsentiert, könnte wie folgt aussehen:
U(A,B) = AB
Wenn Äpfel und Bananen in Isaacs Präferenzen perfekte Komplemente sind, würde die Nutzenfunktion etwa so aussehen:
U(A,B) = MIN,
wobei die MIN-Funktion einfach die kleinere der beiden Zahlen als Wert der Funktion zuweist.
Wenn Äpfel und Bananen perfekte Substitute sind, ist die Nutzenfunktion additiv und würde etwa so aussehen:
U(A,B) = A + B
Eine Klasse von Nutzenfunktionen, die als Cobb-Douglas-Nutzenfunktionen bekannt sind, werden in den Wirtschaftswissenschaften aus zwei Gründen sehr häufig verwendet:
1. Sie stellen „brave“ Präferenzen dar, wie z.B. „mehr ist besser“ und „Vorliebe für Abwechslung“.
2. Sie sind sehr flexibel und können sehr leicht an reale Daten angepasst werden.
Cobb-Douglas-Nutzenfunktionen haben diese Form:
U(A,B) = AαBβ
Da positive monotone Transformationen dieselben Präferenzen darstellen, kann eine solche Transformation verwendet werden, um α + β = 1 zu setzen, was, wie wir später sehen werden, eine bequeme Bedingung ist, die einige Berechnungen im Verbraucherwahlproblem vereinfacht.
Eine andere Möglichkeit, die Nutzenfunktion auf nützliche Weise zu transformieren, besteht darin, den natürlichen Logarithmus der Funktion zu nehmen, wodurch eine neue Funktion entsteht, die wie folgt aussieht:
U(A,B) = αln(A) + βln(B)
Um diese Gleichung herzuleiten, wendet man einfach die Regeln der natürlichen Logarithmen an. Es ist wichtig, hier die Abstraktionsebene im Auge zu behalten. Wir können in der Regel keine spezifischen Nutzenfunktionen erstellen, die die individuellen Präferenzen genau beschreiben. Wahrscheinlich könnte niemand von uns seine eigenen Präferenzen mit einer einzigen Gleichung beschreiben. Solange jedoch die Präferenzen der Verbraucher im Allgemeinen unseren Grundannahmen entsprechen, können wir recht gut Nutzenfunktionen finden, die den realen Verbrauchsdaten entsprechen. Wir werden später im Kurs Beweise dafür sehen.
Tabelle 2.1 fasst die in diesem Abschnitt beschriebenen Präferenzen und Nutzenfunktionen zusammen.
|
Tabelle 2.1 Arten von Präferenzen und die sie repräsentierenden Nutzenfunktionen |
||
|
Präferenzen |
NUTZEN FUNKTION |
TYP DER NUTZENFUNKTION |
|
Liebe zur Vielfalt oder „Wohlverhalten“ |
U(A,B) = AB |
Cobb-Douglas |
|
Vielfaltsliebe oder „Wohlverhalten“ |
U(A,B) = AαBβ |
Cobb-Douglas |
|
Vielfaltsliebe oder „Wohlerzogenheit“ |
U(A,B) = αln(A) + βln(B) |
Natural Log Cobb-Douglas |
|
Perfekte Komplemente |
U(A,B) = MIN |
Min-Funktion |
|
Perfekte Substitute |
U(A,B) = A + B |
Additiv |
2.3. Zusammenhang zwischen Nutzenfunktionen und Indifferenzkurven
LO3: Erläutern Sie, wie man eine Indifferenzkurve aus einer Nutzenfunktion ableitet
Indifferenzkurven und Nutzenfunktionen sind direkt miteinander verbunden. Da Indifferenzkurven Präferenzen grafisch und Nutzenfunktionen mathematisch darstellen, können Indifferenzkurven aus Nutzenfunktionen abgeleitet werden.
Bei univariaten Funktionen wird die abhängige Variable auf der vertikalen Achse und die unabhängige Variable auf der horizontalen Achse aufgetragen, wie z.B. bei y=f(x). Im Gegensatz dazu sind die Graphen von bivariaten Funktionen dreidimensional, wie U=U(A,B). Abbildung 2.1 zeigt einen Graphen von U=A^\frac{1}{2}B^\frac{1}{2}. Dreidimensionale Graphen sind nützlich, um zu verstehen, wie der Nutzen mit steigendem Konsum von A und B zunimmt.
Abbildung 2.1 U=A^\frac{1}{2}B^\frac{1}{2}
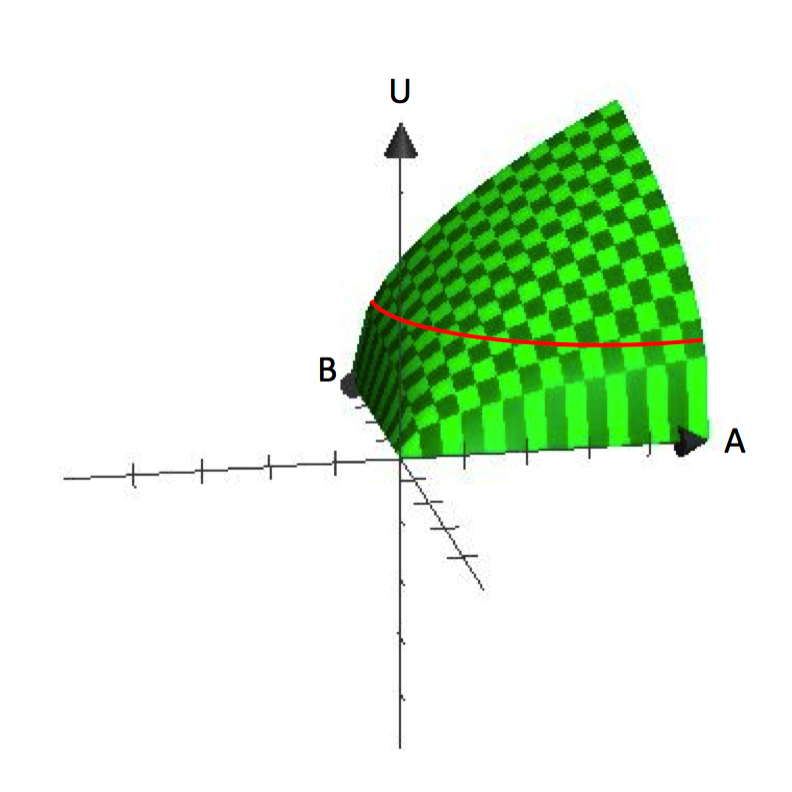
Abbildung 2.1 zeigt deutlich die Annahme, dass die Verbraucher eine Präferenz für Vielfalt haben. Jedes Bündel, das eine bestimmte Menge von A und B enthält, stellt einen Punkt auf der Fläche dar. Die vertikale Höhe der Fläche stellt das Nutzenniveau dar. Indem er sowohl A als auch B erhöht, kann ein Verbraucher höhere Punkte auf der Oberfläche erreichen.
Woher kommen nun die Indifferenzkurven? Erinnern Sie sich daran, dass eine Indifferenzkurve eine Sammlung aller Bündel ist, denen gegenüber ein Verbraucher indifferent ist, in Bezug darauf, welches er konsumieren soll. Mathematisch gesehen bedeutet dies, dass alle Bündel, wenn sie in die Nutzenfunktion eingesetzt werden, denselben Funktionswert ergeben. Wenn wir also einen Wert für den Nutzen, Ū, festlegen und alle Bündel von A und B finden, die diesen Wert erzeugen, definieren wir eine Indifferenzkurve. Dies ist gleichbedeutend mit der Suche nach allen Bündeln, die den Verbraucher auf die gleiche Höhe auf der dreidimensionalen Fläche in Abbildung 2.1 bringen.
Indifferenzkurven sind eine Darstellung der Höhe (des Nutzens) auf einer ebenen Fläche. Sie sind damit analog zu einer Höhenlinie auf einer topographischen Karte. Wenn wir das dreidimensionale Diagramm in den zweidimensionalen Raum – den A- und B-Raum – zurückverlegen, können wir die Höhenlinien/Indifferenzkurven darstellen, die unterschiedliche Höhenlagen oder Nutzwerte repräsentieren. Anhand des Graphen in Abbildung 2.1 kann man bereits sehen, wie diese Nutzenfunktion Indifferenzkurven ergibt, die „eingebogen“ oder konkav zum Ursprung sind.
Die Indifferenzkurven ergeben sich also direkt aus den Nutzenfunktionen und sind eine nützliche Methode, um Nutzenfunktionen in einem zweidimensionalen Graphen darzustellen.
2.4 Ermittlung des Grenznutzens und der Grenzrate der Substitution
LO4: Leiten Sie den Grenznutzen und die Grenzrate der Substitution für typische Nutzenfunktionen ab.
Der Grenznutzen ist der zusätzliche Nutzen, den ein Konsument durch den Konsum einer zusätzlichen Einheit eines Gutes erhält. Mathematisch wird dies ausgedrückt als:
MU_{a}=\frac{\Delta \cup }{\Delta A}
oder die Veränderung des Nutzens durch eine Veränderung der konsumierten Menge von A, wobei Δ eine Veränderung des Wertes des Gutes darstellt. Also,
MU_{a}=\frac{\Delta \cup }{\Delta A}=\frac{\cup (A+\Delta A,B)-U(A,B)}{\Delta A}
Beachten Sie, dass wir, wenn wir den Grenznutzen des Konsums von A untersuchen, B konstant halten.
Der Grenznutzen ist rechnerisch dasselbe wie die partielle Ableitung der Nutzenfunktion nach A:
MU_{A}\frac{\partial U(A,B)}{\partial A}
Betrachten wir einen Verbraucher, der sich hinsetzt, um eine Mahlzeit aus Salat und Pizza zu essen. Nehmen wir an, dass wir die Menge des Salats konstant halten – zum Beispiel ein Salat zum Essen. Erhöhen wir nun die Anzahl der Pizzastücke, nehmen wir an, dass der Nutzen bei 1 Stück 10, bei 2 Stück 18, bei 3 Stück 24 und bei 4 Stück 28 beträgt. Tragen wir diese Zahlen in ein Diagramm ein, bei dem der Nutzen auf der vertikalen Achse und die Pizza auf der horizontalen Achse liegt (Abbildung 2.2).
Abbildung 2.2: Graph und Tabelle des abnehmenden Grenznutzens
|
Pizzastücke |
Nutzen |
Marginaler Utility |
|
1 |
10 |
|
|
2 |
18 |
8 |
|
3 |
24 |
6 |
|
4 |
28 |
4 |
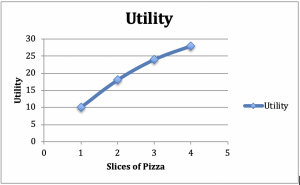
Aus der positiven Steigung der Grafik, können wir den Anstieg des Nutzens durch zusätzliche Pizzastücke erkennen. An der konkaven Form des Graphen können wir ein weiteres gemeinsames Phänomen erkennen: Der zusätzliche Nutzen, den der Verbraucher von jedem zusätzlichen Stück Pizza erhält, nimmt mit der Anzahl der verzehrten Stücke ab.
Die Tatsache, dass der zusätzliche Nutzen mit jedem zusätzlichen Stück Pizza kleiner wird, nennt man das Prinzip des abnehmenden Grenznutzens. Dieses Prinzip gilt für wohlbehaltene Präferenzen, bei denen gemischte Bündel bevorzugt werden.
Die marginale Substitutionsrate (MRS) ist die Menge eines Gutes, die ein Verbraucher bereit ist, aufzugeben, um eine weitere Einheit eines anderen Gutes zu erhalten. Deshalb ist sie dasselbe wie die Steigung der Indifferenzkurve – da wir das Zufriedenheitsniveau konstant halten, bleiben wir auf derselben Indifferenzkurve, wir bewegen uns nur auf ihr, wenn wir ein Gut gegen ein anderes tauschen. Wie viel man bereit ist, von einem Gut gegen ein anderes einzutauschen, hängt vom Grenznutzen der beiden Güter ab.
Wenn man, wie in unserem vorherigen Beispiel, durch den Verzehr eines weiteren Salats seinen Nutzen um 10 erhöht, könnte man bei einem derzeitigen Verzehr von 4 Pizzastücken 2 Pizzastücke aufgeben und von 28 auf 18 Stück kommen. 10 mehr Nutzen durch den Salat und 10 weniger Nutzen durch den Verzicht auf 2 Pizzastücke lassen den Gesamtnutzen unverändert – wir müssen uns also immer noch auf derselben Indifferenzkurve befinden. Wenn man sich entlang der Indifferenzkurve bewegt, muss man der Steigung folgen, d.h. man muss das Gut auf der vertikalen Achse für mehr von dem Gut auf der horizontalen Achse aufgeben, was zu einem negativen Anstieg bei einem positiven Verlauf führt.
Wir können direkt vom Grenznutzen zur MRS übergehen, indem wir die Verbindung zwischen den beiden Konzepten erkennen. In unserem Fall, für eine Nutzenfunktion U=U(A,B) , wird MRS wie folgt dargestellt:
MRS=-\frac{MU_{A}}{MU_{B}}
Beachten Sie, dass wir die Gleichung vereinfachen können, wenn wir sie ersetzen:
MRS=-\frac{MU_{A}}{MU_{B}}=-\frac{\frac{\Delta U}{\Delta A}}{\frac{\Delta U}{\Delta B}}=-\frac{\Delta B}{\Delta A}
Einsetzen der Rechnung ergibt:
MRS=-\frac{\frac{\partial U(A,B)}{\partial A}}{\frac{\partial U(A,B)}{\partial B}}
2.5 Politische Frage
Wir haben in Modul 1 festgestellt, dass die relevante Verbraucherentscheidung zwischen mehr gefahrenen Kilometern und anderem Konsum wahrscheinlich den Standardannahmen über die Verbraucherwahl entspricht. Daher ist die Verwendung der Cobb-Douglas-Nutzenfunktion zur Darstellung eines Verbrauchers, der sowohl gerne Auto fährt als auch andere Güter konsumiert, und der beides als Kompromiss sieht (Geld, das für Benzin ausgegeben wird, ist Geld, das nicht für andere Konsumgüter ausgegeben wird), eine gute Wahl. Es hat auch den Vorteil, dass es sowohl mit den Annahmen übereinstimmt als auch flexibel ist:
U(MD,C)=MD^{a}C^{\beta }
wobei MD = gefahrene Kilometer und C = sonstiger Verbrauch.
Die Funktion selbst kann auf reale Daten übertragen werden, wobei die Parameter und für diesen Markt, den Markt für die mit dem Auto des Verbrauchers gefahrenen Kilometer, geschätzt werden können.
Abbildung 2.3 Diagramm der Indifferenzkurven für das Politikbeispiel
Untersuchung der Politikfragen:
1 . Wären andere Präferenztypen in diesem Beispiel geeigneter?
2. Was müsste für perfekte Komplemente zutreffen, um der geeignete Präferenztyp für die Analyse dieser Politik zu sein?
Was müsste für perfekte Substitute zutreffen? Angesichts der Tatsache, dass wir einen „typischen“ Verbraucher betrachten, der Auto fährt, ist es angemessen, eine „typische“ Nutzenfunktion zu wählen?
4. Raten wir nur, oder haben wir eine theoretische Grundlage, um unsere Wahl von „wohlerzogenen“ Präferenzen oder einer Cobb-Douglas-Nutzenfunktion zu unterstützen?
ZUSAMMENFASSUNG
Rückblick: Themen und verwandte Lernergebnisse
2.1 Nutzenfunktionen
L 2.1: Beschreiben Sie eine Nutzenfunktion
2.2 Nutzenfunktionen und typische Präferenzen
LO 2.2: Identifizieren Sie Nutzenfunktionen anhand der typischen Präferenzen, die sie repräsentieren
2.3. Setzen Sie Nutzenfunktionen und Indifferenzkurven in Beziehung
LO 2.3: Erklären Sie, wie man eine Indifferenzkurve aus einer Nutzenfunktion ableitet
2.4. Finden Sie Grenznutzen und marginale Substitutionsrate
LO 2.4: Leiten Sie Grenznutzen und MRS für typische Nutzenfunktionen ab.
2.5. Policy Question
Learn: Schlüsselbegriffe und Graphen
Bi-variante Funktionen
Kardinal
Konturlinie
Abnehmender Grenznutzen
Funktion
Marginale Substitutionsrate (MRS)
Marginaler Nutzen
Ordinal
Univariate Funktionen
Util
Nutzwert
Nutzwertfunktion
Graphen
3D-Nutzwertfunktion und Konturlinie
Gleichungen
Cobb-Douglas
Perfekte Ergänzungen
Perfekte Substitute