Grundsätze der Satellitenkommunikation

Ein Satellit ist ein Körper, der sich um einen anderen Körper auf einer mathematisch vorhersehbaren Bahn, der sogenannten Umlaufbahn, bewegt. Ein Kommunikationssatellit ist nichts anderes als eine Mikrowellen-Repeaterstation im Weltraum, die für Telekommunikation, Radio und Fernsehen sowie für Internetanwendungen hilfreich ist.

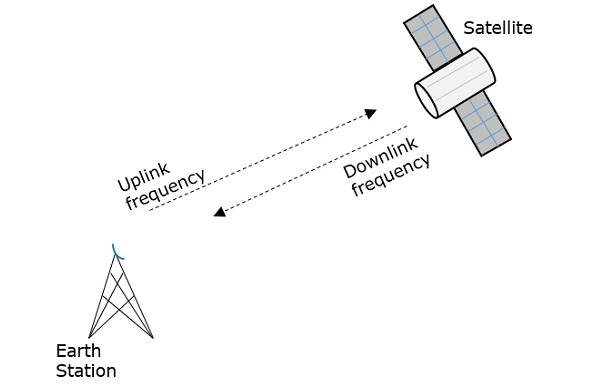
Ein Repeater ist ein Schaltkreis, der die Stärke des empfangenen Signals erhöht und es erneut überträgt. Aber hier arbeitet dieser Repeater als Transponder, der das Frequenzband des gesendeten Signals gegenüber dem empfangenen ändert.

Die Frequenz, mit der das Signal in den Weltraum gesendet wird, nennt man Uplink-Frequenz, während die Frequenz, mit der es vom Transponder gesendet wird, Downlink-Frequenz heißt.

Die folgende Abbildung veranschaulicht dieses Konzept deutlich.

Nun lassen Sie uns einen Blick auf die Vorteile, Nachteile und Anwendungen der Satellitenkommunikation werfen.

Satellitenkommunikation – Vorteile

Es gibt viele Vorteile der Satellitenkommunikation, wie z.B. –

• Flexibilität

• Einfache Installation neuer Schaltkreise

• Entfernungen können leicht überbrückt werden und die Kosten spielen keine Rolle

• Übertragungs Möglichkeiten

• Jeder Winkel der Erde wird abgedeckt

• Der Benutzer kann das Netz kontrollieren

Satellitenkommunikation – Nachteile

Satellitenkommunikation hat folgende Nachteile –

• Die Anfangskosten wie Segment- und Startkosten sind zu hoch.

• Verstopfung der Frequenzen

• Störungen und Ausbreitung

Satellitenkommunikation – Anwendungen

Satellitenkommunikation findet ihre Anwendungen in folgenden Bereichen –

• Im Rundfunkbereich.

• Bei Fernsehübertragungen wie DTH.

• Bei Internetanwendungen wie der Bereitstellung einer Internetverbindung für Datenübertragung, GPS-Anwendungen, Internet-Surfen, usw.

• Für die Sprachkommunikation.

• Für den Forschungs- und Entwicklungssektor, in vielen Bereichen.

• In militärischen Anwendungen und Navigation.

Die Ausrichtung des Satelliten in seiner Umlaufbahn hängt von den drei Gesetzen ab, die als Keplersche Gesetze bezeichnet werden.

Keplersche Gesetze

Johannes Kepler (1571-1630), der astronomische Wissenschaftler, gab 3 revolutionäre Gesetze bezüglich der Bewegung von Satelliten. Die Bahn, die ein Satellit um seinen Ausgangspunkt (die Erde) beschreibt, ist eine Ellipse. Die Ellipse hat zwei Brennpunkte – F1 und F2, wobei die Erde einer von ihnen ist.

Betrachtet man die Entfernung vom Zentrum des Objekts zu einem Punkt auf seiner elliptischen Bahn, dann wird der am weitesten vom Zentrum entfernte Punkt einer Ellipse als Apogäum und der am kürzesten vom Zentrum entfernte Punkt einer Ellipse als Perigäum bezeichnet.

Kepler’s 1. Gesetz

Kepler’s 1. Gesetz besagt, dass „jeder Planet auf einer elliptischen Bahn um die Sonne kreist, mit der Sonne als einem ihrer Brennpunkte.“ So bewegt sich auch ein Satellit auf einer elliptischen Bahn mit der Erde als einem ihrer Brennpunkte.

Die Hauptachse der Ellipse wird mit „a“ und die Nebenachse mit „b“ bezeichnet. Daher kann die Exzentrizität e dieses Systems geschrieben werden als –

$$e = \frac{\sqrt{a^{2}-b^{2}}}{a}$$

• Exzentrizität (e) – Sie ist der Parameter, der den Unterschied in der Form der Ellipse im Vergleich zu der eines Kreises definiert.

• Semi-Hauptachse (a) – Sie ist der längste Durchmesser, der die beiden Brennpunkte entlang des Zentrums verbindet und die beiden Scheitelpunkte (die am weitesten vom Zentrum entfernten Punkte einer Ellipse) berührt.

• Halb-Minor-Achse (b) – Sie ist der kürzeste Durchmesser, der durch das Zentrum gezogen wird und beide Perigäen (kürzeste Punkte einer Ellipse vom Zentrum) berührt.

Diese sind in der folgenden Abbildung gut beschrieben.

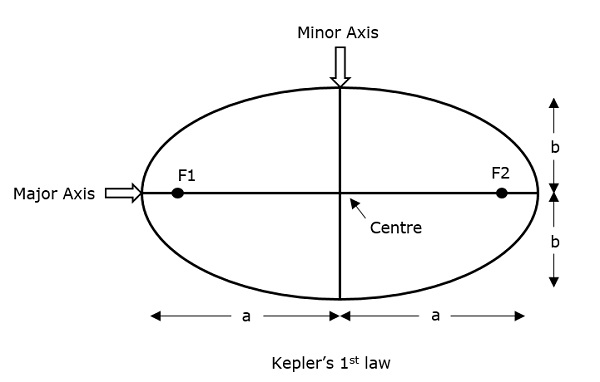
Für eine elliptische Bahn ist es immer wünschenswert, dass die Exzentrizität zwischen 0 und 1 liegt, d.d. h. 0 < e < 1, denn wenn e Null wird, ist die Bahn nicht mehr elliptisch, sondern wird in eine Kreisbahn umgewandelt.

Keplersches 2. Gesetz

Das 2. Gesetz von Kepler besagt: „Bei gleichen Zeitabständen ist die vom Satelliten überstrichene Fläche in Bezug auf den Erdmittelpunkt gleich.“

Das kann man verstehen, wenn man die folgende Abbildung betrachtet.

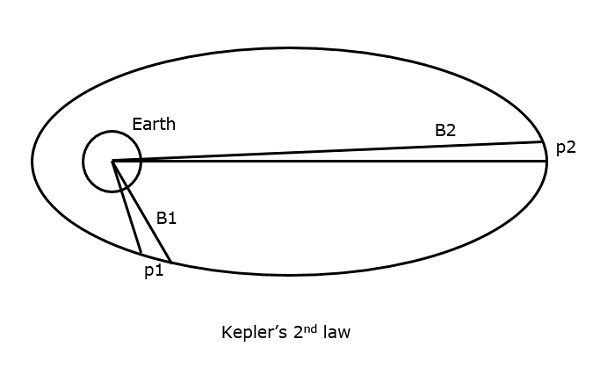
Angenommen, der Satellit legt in demselben Zeitintervall p1 und p2 Entfernungen zurück, dann sind die Flächen B1 und B2, die in beiden Fällen zurückgelegt werden, gleich.

Keplersches 3. Gesetz

Keplersches 3. Gesetz besagt: „Das Quadrat der Periodendauer der Umlaufbahn ist proportional zum Kubus der mittleren Entfernung zwischen den beiden Körpern.“

Dies kann mathematisch geschrieben werden als

$$T^{2}\:\alpha\:\:a^{3}$$

Das impliziert

$T^{2} = \frac{4\pi ^{2}}{GM}a^{3}$$

Wobei $\frac{4\pi ^{2}}{GM}$ die Proportionalitätskonstante ist (nach der Newtonschen Mechanik)

$$T^{2} = \frac{4\pi ^{2}}{\mu}a^{3} $$

Wobei μ = die geozentrische Gravitationskonstante der Erde ist, i.d. h. Μ = 3.986005 × 1014 m3/sec2

$$1 = \links ( \frac{2\pi}{T} \rechts )^{2}\frac{a^{3}}{\mu}$$

$$1 = n^{2}\frac{a^{3}}{\mu}\:\:\:\Rightarrow \:\:a^{3} = \frac{\mu}{n^{2}}$$

Wobei n = die mittlere Bewegung des Satelliten in Radiant pro Sekunde

Die Bahnfunktion von Satelliten wird mit Hilfe dieser Keplerschen Gesetze berechnet.

Neben diesen Gesetzen gibt es eine wichtige Sache, die zu beachten ist. Ein Satellit erfährt, wenn er um die Erde kreist, eine Anziehungskraft von der Erde, die Gravitationskraft. Außerdem erfährt er eine gewisse Anziehungskraft von der Sonne und dem Mond. Es gibt also zwei Kräfte, die auf ihn wirken. Sie sind –

• Zentripetalkraft – Die Kraft, die dazu neigt, ein Objekt, das sich auf einer Bahn bewegt, auf sich selbst zu ziehen, wird Zentripetalkraft genannt.

• Zentrifugalkraft – Die Kraft, die dazu neigt, ein Objekt, das sich auf einer Bahn bewegt, von seiner Position wegzustoßen, wird Zentrifugalkraft genannt.

Ein Satellit muss also diese beiden Kräfte ausbalancieren, um sich in seiner Umlaufbahn zu halten.

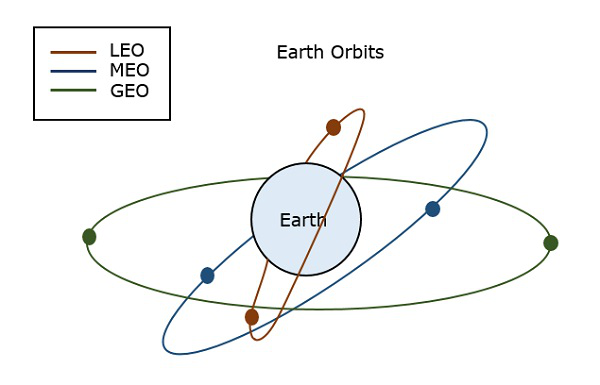
Erdumlaufbahnen

Ein Satellit muss, wenn er in den Weltraum geschossen wird, in einer bestimmten Umlaufbahn platziert werden, um einen bestimmten Weg für seine Drehung zu ermöglichen, damit er erreichbar bleibt und seinen Zweck erfüllt, sei es wissenschaftlich, militärisch oder kommerziell. Solche Umlaufbahnen, die den Satelliten in Bezug auf die Erde zugewiesen werden, werden als Erdumlaufbahnen bezeichnet. Die Satelliten auf diesen Bahnen sind Erdumlaufsatelliten.

Die wichtigsten Arten von Erdumlaufbahnen sind –

• Geosynchrone Erdumlaufbahn

• Mittlere Erdumlaufbahn

• Niedrige Erdumlaufbahn

Geosynchrone Erdumlaufbahn Satelliten

Eine Geo-Synchronous Earth Orbit (GEO) ist ein Satellit, der sich in einer Höhe von 22,300 Meilen über der Erde befindet. Diese Umlaufbahn ist mit einem realen Seitentag (d.h. 23 Stunden 56 Minuten) synchronisiert. Diese Umlaufbahn kann eine Neigung und Exzentrizität aufweisen. Sie muss nicht kreisförmig sein. Diese Bahn kann an den Polen der Erde geneigt sein. Von der Erde aus betrachtet erscheint sie jedoch stationär.

Die gleiche geosynchrone Umlaufbahn, wenn sie kreisförmig und in der Äquatorebene liegt, wird als geostationäre Umlaufbahn bezeichnet. Diese Satelliten befinden sich in einer Höhe von 35.900 km (wie geosynchron) über dem Erdäquator und rotieren in Bezug auf die Erdrichtung (von West nach Ost). Diese Satelliten werden als stationär in Bezug auf die Erde betrachtet, was der Name schon andeutet.

Geo-stationäre Erdumlaufbahnen werden für Wettervorhersagen, Satellitenfernsehen, Satellitenradio und andere Arten der globalen Kommunikation verwendet.

Die folgende Abbildung zeigt den Unterschied zwischen geosynchronen und geostationären Umlaufbahnen. Die Rotationsachse zeigt die Bewegung der Erde an.

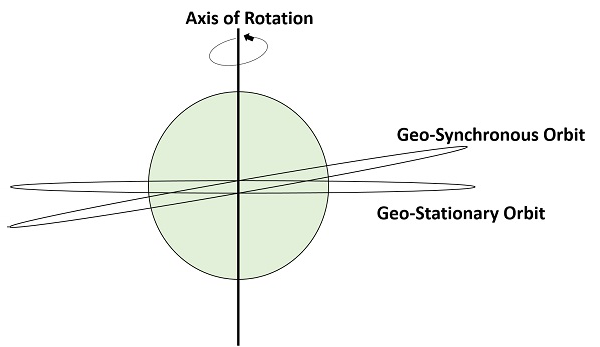
Hinweis – Jede geostationäre Umlaufbahn ist eine geosynchrone Umlaufbahn. Aber jeder geosynchrone Orbit ist KEIN geostationärer Orbit.

Medium Earth Orbit Satellites

Medium Earth Orbit (MEO) Satellitennetzwerke kreisen in einer Entfernung von etwa 8000 Meilen von der Erdoberfläche. Signale, die von einem MEO-Satelliten gesendet werden, legen eine kürzere Strecke zurück. Dies führt zu einer besseren Signalstärke auf der Empfangsseite. Dies zeigt, dass auf der Empfangsseite kleinere, leichtere Empfangsgeräte verwendet werden können.

Da das Signal eine kürzere Strecke zum und vom Satelliten zurücklegt, gibt es eine geringere Übertragungsverzögerung. Die Übertragungsverzögerung kann als die Zeit definiert werden, die ein Signal benötigt, um zu einem Satelliten zu gelangen und wieder zu einer Empfangsstation zurückzukehren.

Für die Echtzeitkommunikation gilt: Je kürzer die Übertragungsverzögerung, desto besser ist das Kommunikationssystem. Benötigt ein GEO-Satellit beispielsweise 0,25 Sekunden für einen Hin- und Rückflug, so benötigt ein MEO-Satellit weniger als 0,1 Sekunden für die gleiche Strecke. MEO-Satelliten arbeiten im Frequenzbereich von 2 GHz und darüber.

Satelliten in niedriger Erdumlaufbahn

Die Satelliten in niedriger Erdumlaufbahn (Low Earth Orbit, LEO) werden hauptsächlich in drei Kategorien eingeteilt, nämlich in kleine LEOs, große LEOs und Mega-LEOs. LEOs kreisen in einer Entfernung von 500 bis 1000 Meilen über der Erdoberfläche.

Durch diese relativ kurze Entfernung verringert sich die Übertragungsverzögerung auf nur 0,05 Sekunden. Dadurch wird der Bedarf an empfindlichen und sperrigen Empfangsgeräten weiter reduziert. Kleine LEOs werden im 800-MHz-Bereich (0,8 GHz) arbeiten. Big LEOs werden im Bereich von 2 GHz oder darüber betrieben, und Mega-LEOs arbeiten im Bereich von 20-30 GHz.

Die höheren Frequenzen, die mit Mega-LEOs verbunden sind, führen zu einer höheren Informationskapazität und ermöglichen eine Videoübertragung in Echtzeit mit geringer Verzögerung.

Die folgende Abbildung zeigt die Pfade von LEO, MEO und GEO.