In dieser Lektion zeigen wir eine einfache Strategie zur Lösung der folgenden Aufgabe: wie man den Flächeninhalt eines gleichschenkligen Dreiecks findet.
Wenden wir einige der Eigenschaften, die wir bisher bewiesen haben, in der folgenden Geometrieaufgabe an:
Problem
In einem gleichschenkligen Dreieck ΔABC mit der Schenkellänge 10 ist die Höhe zur Basis gleich zwei Dritteln der Basis. Finde den Flächeninhalt des Dreiecks.
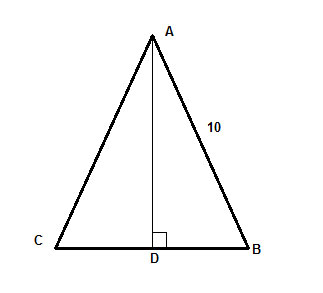
Strategie
Um diese Aufgabe zu lösen, arbeiten wir rückwärts von dem, was wir tun müssen.
Wir müssen den Flächeninhalt des Dreiecks finden, von dem wir wissen, dass er durch die Formel (Basis mal Höhe)/2 gegeben ist.
Ein Problem, das wir haben, ist, dass wir weder die Basislänge noch die Höhe kennen. Aber wir kennen das Verhältnis zwischen ihnen, das uns einen Hinweis darauf gibt, was wir tun müssen. Nennen wir die Länge der Basis, BC, x.
Dann wissen wir, dass die Höhe, AD, 2x/3 ist, wie in der Aufgabe angegeben.
Die Antwort, die wir suchen, ist also (Basis mal Höhe)/2, oder x mal 2x/3, geteilt durch zwei.
Aber wie finden wir x? Es gibt zwei zusätzliche Dinge, die uns in der Aufgabe gegeben wurden, die wir aber noch nicht benutzt haben – die Länge des Schenkels (10) und die Tatsache, dass dies ein gleichschenkliges Dreieck ist. Wahrscheinlich müssen wir diese beiden Dinge verwenden, um das Problem zu lösen.
Lassen Sie uns die Eigenschaften von gleichschenkligen Dreiecken überprüfen. Eine Sache, die sofort ins Auge springen sollte, ist, dass, wie wir gezeigt haben, in einem gleichschenkligen Dreieck die Höhe zur Basis die Basis halbiert, also CD=DB=x/2.
Schließlich ist AD die Höhe, was bedeutet, dass der Winkel ∠ADC ein rechter Winkel ist, und wir haben ein rechtwinkliges Dreieck, ΔADC, dessen Hypotenuse wir kennen (10) und mit dem wir die Schenkel mit Hilfe des Satzes von Pythagoras finden können, c2 =a2+b2,
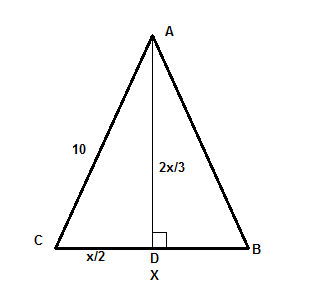
wobei c= 10 ,a = x/2 und b=2x/3 . Und schon sind wir fertig, der Rest ist nur noch algebraisches Lösen für x.
Beweis: Flächeninhalt eines gleichschenkligen Dreiecks
(1) ΔADC ist rechtwinkliges Dreieck //gegeben, da AD die Höhe zur Basis ist
(2) AC2 =CD2 + AD2 //Pythagoreischer Lehrsatz
(3) AC= 10 //gegeben
(4) CB = x
(5) CD = x/2 //Höhe zur Basis im gleichschenkligen Dreieck halbiert die Basis
(6) AD = 2x/3 //gegeben
(7) 102 = (x/2)2 + (2x/3)2 //Einsetzen in (2)
(8) 100 = x2/4+4×2/9 //Vereinfachen
(9) 100*36 = 9×2 +16×2 //Multiplizieren beider Seiten mit 36
(10) 100*36 = 25×2 //Zusammenfassen ähnlicher Terme