Antwort 7 – 7 – 7 = 73 Das heißt „sieben hoch drei“

Verstehen von Exponenten und Quadratwurzeln

Lernziel(e)

– Ausdrücke, die Exponenten enthalten, auswerten.

– Wiederholte Faktoren mit Hilfe der Exponentialschreibweise schreiben.

– Die Quadratwurzel eines perfekten Quadrats finden.

Exponenten stellen eine besondere Art dar, wiederholte Multiplikationen zu schreiben. Zahlen, die auf diese Weise geschrieben werden, haben eine bestimmte Form, wobei jeder Teil wichtige Informationen über die Zahl liefert. Durch die Verwendung von Exponenten kann auch viel Platz gespart werden. Die umgekehrte Operation der Multiplikation einer Zahl mit sich selbst wird Quadratwurzel aus einer Zahl genannt. Diese Operation ist hilfreich bei Problemen mit dem Flächeninhalt eines Quadrats.

Die Exponentialschreibweise ist eine besondere Art, sich wiederholende Faktoren zu schreiben, zum Beispiel 7 – 7. Die Exponentialschreibweise besteht aus zwei Teilen. Der eine Teil der Notation wird als Basis bezeichnet. Die Basis ist die Zahl, die mit sich selbst multipliziert wird. Der andere Teil der Schreibweise ist der Exponent oder die Potenz. Dies ist die kleine Zahl, die rechts von der Basis hochgeschrieben wird. Der Exponent oder die Potenz gibt an, wie oft die Basis als Faktor bei der Multiplikation verwendet werden soll. In diesem Beispiel kann 7 – 7 als 72 geschrieben werden, wobei 7 die Basis und 2 der Exponent ist. Der Exponent 2 bedeutet, dass es zwei Faktoren gibt.

72 = 7 – 7 = 49

Sie können 72 als „sieben zum Quadrat“ lesen. Das liegt daran, dass die Multiplikation einer Zahl mit sich selbst als „Quadrieren einer Zahl“ bezeichnet wird. Ebenso wird das Erhöhen einer Zahl auf eine Potenz von 3 als „Kubieren der Zahl“ bezeichnet. Du kannst 73 als „sieben kubiert“ lesen.

Du kannst 25 als „zwei hoch fünf“ oder „zwei hoch fünf“ lesen. Lesen Sie 84 als „acht hoch vier“ oder „acht hoch vier“. Dieses Format kann für jede Zahl verwendet werden, die in Exponentialschreibweise geschrieben ist. 63 wird meist als „sechs hoch drei“ gelesen, kann aber auch als „sechs hoch drei“ oder „sechs hoch drei“ gelesen werden.

Um den Wert einer in Exponentialform geschriebenen Zahl zu ermitteln, schreiben Sie die Zahl als wiederholte Multiplikation um und führen die Multiplikation durch. Zwei Beispiele werden unten gezeigt.

Finde den Wert von 43.

A) 12

B) 64

C) 256

D) 43

Wenn man wiederholte Multiplikation in Exponentialschreibweise schreibt, kann man Zeit und Platz sparen. Betrachten wir das Beispiel 5 – 5 – 5 – 5. Wir können die Exponentialschreibweise verwenden, um diese wiederholte Multiplikation als 54 zu schreiben. Da die 5 multipliziert wird, wird sie als Basis geschrieben. Da die Basis bei der Multiplikation viermal verwendet wird, ist der Exponent 4. Der Ausdruck 5 – 5 – 5 – 5 kann in der Exponentialschreibweise in 54 umgeschrieben werden und lautet „fünf hoch vier“ oder „fünf hoch 4“.

Um die wiederholte Multiplikation derselben Zahl in Exponentialschreibweise zu schreiben, schreibt man zunächst die zu multiplizierende Zahl als Basis. Zähle dann, wie oft diese Zahl bei der Multiplikation verwendet wird, und schreibe diese Zahl als Exponent. Achte darauf, die Zahlen zu zählen, nicht die Multiplikationszeichen, um den Exponenten zu bestimmen.

Schreibe 10 – 10 – 10 – 10 – 10 – 10 in Exponentialschreibweise.

A) 1.000.000

B) 60

C) 105

D) 106

Wie du bereits gesehen hast, wird 52 „fünf zum Quadrat“ genannt. „Fünf zum Quadrat“ bedeutet, dass man fünf mit sich selbst multipliziert. In der Mathematik nennt man das Multiplizieren einer Zahl mit sich selbst „Quadrieren“ der Zahl. Das Ergebnis der Quadrierung einer ganzen Zahl nennen wir ein Quadrat oder ein perfektes Quadrat. Ein perfektes Quadrat ist jede Zahl, die als ganze Zahl hoch 2 geschrieben werden kann. 9 ist zum Beispiel ein perfektes Quadrat. Eine perfekte Quadratzahl kann als Quadrat dargestellt werden, wie unten gezeigt. Wir sehen, dass 1, 4, 9, 16, 25 und 36 Beispiele für perfekte Quadrate sind.

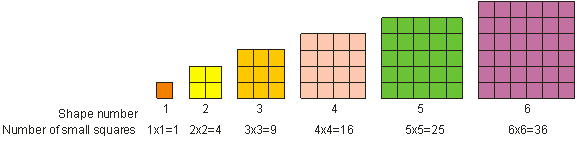
Um eine Zahl zu quadrieren, multipliziert man die Zahl mit sich selbst. 3 zum Quadrat = 32 = 3 – 3 = 9.

Nachfolgend einige weitere Beispiele für perfekte Quadrate.

Die umgekehrte Operation des Quadrierens einer Zahl nennt man die Suche nach der Quadratwurzel einer Zahl. Die Suche nach der Quadratwurzel ist wie die Frage: „Welche Zahl mit sich selbst multipliziert ergibt diese Zahl?“ Die Quadratwurzel von 25 ist 5, weil 5 mit sich selbst multipliziert 25 ergibt. Quadratwurzeln werden mit einem mathematischen Symbol geschrieben, das Radikalzeichen genannt wird und wie folgt aussieht: . Die „Quadratwurzel aus 25“ wird geschrieben.

Finde .

A) 6

B) 18

C) 72

D) 7

Die Exponentialschreibweise ist eine Kurzform für die wiederholte Multiplikation der gleichen Zahl. Eine in Exponentialschreibweise geschriebene Zahl hat eine Basis und einen Exponenten, und jeder dieser Teile liefert Informationen für die Ermittlung des Wertes des Ausdrucks. Die Basis gibt an, welche Zahl wiederholt multipliziert wird, und der Exponent gibt an, wie oft die Basis bei der Multiplikation verwendet wird. Die Exponenten 2 und 3 haben besondere Namen. Das Erhöhen einer Basis auf eine Potenz von 2 wird als „Quadrieren“ einer Zahl bezeichnet. Das Erhöhen einer Basis auf eine Potenz von 3 wird als „Kubieren“ einer Zahl bezeichnet. Die Umkehrung des Quadrierens einer Zahl ist die Ermittlung der Quadratwurzel einer Zahl. Um die Quadratwurzel einer Zahl zu finden, frage dich: „Welche Zahl kann ich mit sich selbst multiplizieren, um diese Zahl zu erhalten?“