A Concise Introduction to Logic

9.1 Ein historisches Beispiel

Der Philosoph David Hume (1711-1776) ist als brillanter skeptischer Empiriker bekannt. Eine Person ist ein Skeptiker in Bezug auf ein bestimmtes Thema, wenn sie einerseits sehr strenge Maßstäbe an das, was Wissen über dieses Thema ausmacht, anlegt und andererseits glaubt, dass wir diese strengen Maßstäbe nicht erfüllen können. Der Empirismus vertritt die Auffassung, dass wir unser Wissen in erster Linie durch Erfahrung, insbesondere durch Sinneserfahrungen, gewinnen. In seinem Buch An Inquiry Concerning Human Understanding (Eine Untersuchung über den menschlichen Verstand) legt Hume seine Grundsätze für das Wissen dar und rät uns dann, unsere Bibliotheken aufzuräumen:

Wenn wir, von diesen Grundsätzen überzeugt, über Bibliotheken herfallen, welche Verwüstung müssen wir dann anrichten? Wenn wir zum Beispiel einen Band der Göttlichkeit oder der Schulmetaphysik in die Hand nehmen, fragen wir uns: Enthält er irgendeine abstrakte Argumentation über Menge oder Zahl? Nein. Enthält es irgendwelche experimentellen Überlegungen über Tatsachen und Existenz? Nein. Verbrennt sie dann, denn sie kann nichts als Sophisterei und Illusion enthalten.

Hume war der Ansicht, dass die einzigen Quellen des Wissens logische oder mathematische Überlegungen (die er oben „abstrakte Überlegungen über Quantität oder Zahl“ nennt) oder Sinneserfahrungen („experimentelle Überlegungen über Tatsachen und Existenz“) sind. Hume argumentiert, dass jede Behauptung, die nicht auf der einen oder anderen Methode beruht, wertlos ist.

Wir können Humes Argument folgendermaßen rekonstruieren. Angenommen, t ist ein Thema, über das wir behaupten, Wissen zu haben. Nehmen wir an, dass wir dieses Wissen nicht durch Erfahrung oder Logik erlangt haben. Auf Englisch geschrieben, können wir sein Argument folgendermaßen rekonstruieren:

Wir haben Wissen über t, wenn und nur wenn unsere Behauptungen über t aus experimentellem Denken oder aus Logik oder Mathematik gelernt wurden.

Unsere Behauptungen über t werden nicht durch experimentelles Denken gelernt.

Unsere Behauptungen über t werden nicht durch Logik oder Mathematik gelernt.

Wir haben kein Wissen über t.

Was bedeutet dieser Satz „wenn und nur wenn“? Philosophen sind der Meinung, dass er und mehrere synonyme Ausdrücke häufig in der Argumentation verwendet werden. Wenn wir „if and only“ vorerst unerklärt lassen, können wir den folgenden Übersetzungsschlüssel verwenden, um das Argument in einer Mischung aus unserer Aussagenlogik und dem Englischen aufzuschreiben.

P: Wir haben Wissen über t.

Q: Unsere Behauptungen über t sind aus experimentellen Überlegungen gelernt.

R: Unsere Aussagen über t sind aus der Logik oder der Mathematik gelernt.

Und so haben wir:

P wenn und nur wenn (QvR)

¬Q

¬R

¬P

Unsere Aufgabe ist es, unserer logischen Sprache ein Äquivalent zu „wenn und nur wenn“ hinzuzufügen. Dann können wir diese Neuformulierung des Humeschen Arguments auswerten.

9.2 Das Bikonditional

Bevor wir ein Symbol einführen, das gleichbedeutend ist mit „wenn und nur wenn“, und dann seine Syntax und Semantik darlegen, sollten wir mit einer Feststellung beginnen. Eine Formulierung wie „P wenn und nur wenn Q“ scheint eine verkürzte Form von „P wenn Q und P nur wenn Q“ zu sein. Sobald wir dies bemerken, müssen wir nicht mehr versuchen, die Bedeutung von „if and only if“ mit Hilfe unseres Fachwissens über die englische Sprache zu ermitteln. Stattdessen können wir die Bedeutung von „if and only if“ anhand unserer bereits strengen Definitionen von „if“, „and“ und „only if“ erkennen. Konkret wird „P if Q and P only if Q“ mit „((Q→P)^(P→Q))“ übersetzt. (Wenn Ihnen das unklar ist, gehen Sie zurück und lesen Sie Abschnitt 2.2.) Erstellen wir nun eine Wahrheitstabelle für diese Formel.

P	Q	(Q → P)	(P → Q)	((Q→P)^(P→Q))
T	T	T	T	T
T	F	T	F	F
F	T	F	T	F
F	F	T	T	T

Wir haben die Semantik für „wenn und nur wenn“ festgelegt. Wir können nun ein neues Symbol für diesen Ausdruck einführen. Es ist üblich, den Doppelpfeil „↔“ zu verwenden. Wir können nun die Syntax und Semantik von „↔“ ausdrücken.

Wenn Φ und Ψ Sätze sind, dann

(Φ↔Ψ)

ist ein Satz. Diese Art von Satz wird typischerweise „biconditional“ genannt.

Die Semantik ist durch die folgende Wahrheitstabelle gegeben.

Φ	Ψ	(Φ↔Ψ)
T	T	T
T	F	F
F	T	F
F	F	T

Ein erfreuliches Ergebnis unserer Darstellung des Bikonditionals ist, dass es uns erlaubt, den syntaktischen Begriff der logischen Äquivalenz prägnant zu erklären. Wir sagen, dass zwei Sätze Φ und Ψ „äquivalent“ oder „logisch äquivalent“ sind, wenn (Φ↔Ψ) ein Theorem ist.

9.3 Alternative Phrasen

Im Englischen scheint es mehrere Phrasen zu geben, die in der Regel die gleiche Bedeutung haben wie das Bikonditional. Jeder der folgenden Sätze würde mit (P↔Q) übersetzt werden.

P if and only if Q.

P just in case Q.

P is necessary and sufficient for Q.

P is equivalent to Q.

9.4 Argumentieren mit dem Bikonditional

Wie können wir mit einem Bikonditional argumentieren? Auf den ersten Blick scheint es wenig hilfreich zu sein. Wenn ich weiß, dass (P↔Q), dann weiß ich, dass P und Q denselben Wahrheitswert haben, aber aus diesem Satz allein weiß ich nicht, ob sie beide wahr oder falsch sind. Dennoch können wir die Semantik des Zweibedingungssatzes nutzen, um festzustellen, dass wir den Wahrheitswert des anderen Satzes ableiten können, wenn wir auch den Wahrheitswert eines der Sätze kennen, die den Zweibedingungssatz bilden. Dies legt einen einfachen Satz von Regeln nahe. Es handelt sich eigentlich um vier Regeln, aber wir fassen sie unter dem Namen „Äquivalenz“ zusammen:

und

und

und

Was ist, wenn wir stattdessen versuchen, ein Bikonditional zu zeigen? Hier können wir zu der Einsicht zurückkehren, dass das Bikonditional (Φ↔Ψ) äquivalent zu ((Φ→Ψ)^(Ψ→Φ)) ist. Wenn wir sowohl (Φ→Ψ) als auch (Ψ→Φ) beweisen können, wissen wir, dass (Φ↔Ψ) wahr sein muss.

Wir können diese Regel „bicondition“ nennen. Sie hat die folgende Form:

(Φ→Ψ)

(Ψ→Φ)

(Φ↔Ψ)

Das bedeutet, dass wir oft, wenn wir eine bikonditionale Bedingung beweisen wollen, zwei bedingte Ableitungen vornehmen, um zwei Konditionale abzuleiten, und dann die bikonditionale Regel verwenden. Das heißt, dass viele Beweise von Bikonditionalen die folgende Form haben:

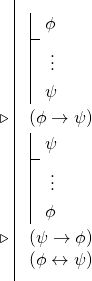
9.5 Zurück zu Hume

Wir können nun sehen, ob wir Humes Argument beweisen können. Da wir nun das neue Symbol der zwei Bedingungen haben, können wir einen direkten Beweis mit unseren drei Prämissen beginnen.

Wir haben bereits festgestellt, dass wir denken, dass (QvR) falsch ist, weil ¬Q und ¬R. Beweisen wir also ¬(QvR). Dieser Satz kann nicht direkt bewiesen werden, da die Voraussetzungen gegeben sind, die wir haben; und er kann nicht mit einem bedingten Beweis bewiesen werden, da er kein Konditional ist. Versuchen wir es also mit einem indirekten Beweis. Wir glauben, dass ¬(QvR) wahr ist, also nehmen wir die Verneinung dieses Satzes an und zeigen einen Widerspruch.

Hume’s Argument, zumindest wie wir es rekonstruiert haben, ist gültig.

Ist Hume’s Argument stichhaltig? Ob es stichhaltig ist, hängt von der obigen ersten Prämisse ab (da die zweite und dritte Prämisse Abstraktionen über ein Thema t sind). Insbesondere hängt es von der Behauptung ab, dass wir etwas nur dann wissen, wenn wir es mit einem Experiment oder mit Logik beweisen können. Hume argumentiert, dass wir Behauptungen, die nicht auf Experimenten und Beobachtungen oder auf Logik und Mathematik beruhen, misstrauen sollten – ja, wir sollten Texte verbrennen. Aber bedenken Sie diese Behauptung: Wir haben Wissen über ein Thema t, wenn und nur wenn unsere Behauptungen über t aus Experimenten oder unsere Behauptungen über t aus Logik oder Mathematik gelernt wurden.

Hat Hume diese Behauptung durch Experimente entdeckt? Oder entdeckte er sie durch die Logik? Welches Schicksal würde Humes Buch erleiden, wenn wir seinen Rat befolgten?

9.6 Einige Beispiele

Es kann hilfreich sein, einige Theoreme zu beweisen, die das Bikonditional benutzen, um zu zeigen, wie wir mit dem Bikonditional argumentieren können.

Hier ist ein nützliches Prinzip. Wenn zwei Sätze den gleichen Wahrheitswert haben wie ein dritter Satz, dann haben sie den gleichen Wahrheitswert wie jeder andere. Wir formulieren dies als (((P↔Q)^(R↔Q))→(P↔R)). Um das Argumentieren mit dem Bikonditional zu veranschaulichen, wollen wir diesen Satz beweisen.

Dieser Satz ist ein Konditional und erfordert daher eine konditionale Ableitung. Der Folgesatz des Konditionalsatzes ist ein Bikonditional, also werden wir voraussichtlich zwei bedingte Ableitungen benötigen, eine zum Beweis von (P→R) und eine zum Beweis von (R→P). Der Beweis wird wie folgt aussehen. Studieren Sie ihn genau.

Wir haben bereits die Prinzipien erwähnt, die wir mit dem Mathematiker Augustus De Morgan (1806-1871) in Verbindung bringen und die heute „De Morgan’s Laws“ oder die „De Morgan Equivalences“ genannt werden. Es handelt sich dabei um die Erkenntnis, dass ¬(PvQ) und (¬P^¬Q) äquivalent sind, und auch, dass ¬(P^Q) und (¬Pv¬Q) äquivalent sind. Wir können diese nun mit dem Bikonditional ausdrücken. Die folgenden sind Theoreme unserer Logik:

(¬(PvQ)↔(¬P^¬Q))

(¬(P^Q)↔(¬Pv¬Q))

Wir werden das zweite dieser Theoreme beweisen. Dies ist vielleicht der schwierigste Beweis, den wir bisher gesehen haben; er erfordert verschachtelte indirekte Beweise und eine gehörige Portion Cleverness, um herauszufinden, was der relevante Widerspruch sein wird.

9.7 Theoreme verwenden

Jeder Satz unserer Logik ist semantisch gesehen eine von drei Arten. Er ist entweder eine Tautologie, ein widersprüchlicher Satz oder ein kontingenter Satz. Wir haben bereits „Tautologie“ (ein Satz, der wahr sein muss) und „kontradiktorischer Satz“ (ein Satz, der falsch sein muss) definiert. Ein Kontingenzsatz ist ein Satz, der weder eine Tautologie noch ein kontradiktorischer Satz ist. Ein kontingenter Satz ist also ein Satz, der wahr oder falsch sein könnte.

Hier ist ein Beispiel für jede Art von Satz:

(Pv¬P)

(P↔¬P)

P

Der erste Satz ist eine Tautologie, der zweite ist ein kontradiktorischer Satz und der dritte ist kontingent. Wir können dies mit einer Wahrheitstabelle sehen.

P	¬P	(Pv¬P)	(P↔¬P)	P
T	F	T	F	T
F	T	T	F	F

Beachte, dass die Negation einer Tautologie ein Widerspruch ist, die Negation eines Widerspruchs eine Tautologie ist und die Negation eines Kontingenzsatzes ein Kontingenzsatz ist.

¬(Pv¬P)

¬(P↔¬P)

¬P

P	¬P	(Pv¬P)	¬(Pv¬P)	(P↔¬P)	¬(P↔¬P)
T	F	T	F	F	T
F	T	T	F	F	T

Ein Moment des Nachdenkens wird zeigen, dass es eine ziemliche Katastrophe wäre, wenn entweder ein widersprüchlicher Satz oder ein kontingenter Satz ein Theorem unserer Aussagenlogik wäre. Unsere Logik wurde entwickelt, um nur gültige Argumente hervorzubringen. Wir haben festgestellt, dass Argumente, die keine Prämissen haben, Schlussfolgerungen haben sollten, die wahr sein müssen (dies folgt wiederum daraus, dass ein Satz, der ohne Prämissen bewiesen werden kann, mit beliebigen Prämissen bewiesen werden kann, und daher besser wahr sein sollte, egal welche Prämissen wir verwenden). Wäre ein Satz widersprüchlich, so wüssten wir, dass wir eine Unwahrheit beweisen könnten. Wäre ein Satz kontingent, dann könnten wir manchmal eine Unwahrheit beweisen (d.h. wir könnten einen Satz beweisen, der unter bestimmten Bedingungen falsch ist). Und da wir die indirekte Ableitung als Beweismethode angenommen haben, folgt daraus, dass wir, sobald wir einen Widerspruch oder einen widersprüchlichen Satz in einem Argument haben, alles beweisen können.

Theoreme können uns in Argumenten sehr nützlich sein. Nehmen wir an, wir wissen, dass weder Smith noch Jones nach London gehen werden, und wir wollen daher beweisen, dass Jones nicht nach London gehen wird. Wenn wir uns erlauben würden, eines von De Morgans Theoremen zu verwenden, könnten wir das Argument schnell aus der Welt schaffen. Nehmen wir den folgenden Schlüssel an:

P: Smith wird nach London gehen.

Q: Jones wird nach London gehen.

Und wir haben das folgende Argument:

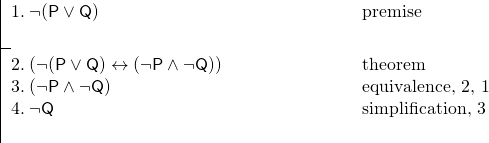
Dieser Beweis wurde durch die Verwendung des Theorems in Zeile 2 sehr einfach gemacht.

Dabei sind zwei Dinge zu beachten. Erstens sollten wir uns dies erlauben, denn wenn wir wissen, dass ein Satz ein Theorem ist, dann wissen wir, dass wir dieses Theorem in einem Teilbeweis beweisen können. Das heißt, wir könnten die obige Zeile 2 durch einen langen Teilbeweis ersetzen, der (¬(P v Q)↔(¬P ^ ¬Q)) beweist, den wir dann verwenden könnten. Aber wenn wir sicher sind, dass (¬(P v Q)↔(¬P ^ ¬Q)) ein Theorem ist, sollten wir diesen Beweis nicht jedes Mal wiederholen müssen, wenn wir das Theorem verwenden wollen.

Das zweite Problem, das wir erkennen sollten, ist subtiler. Es gibt unendlich viele Sätze in der Form unseres Satzes, und wir sollten in der Lage sein, auch diese zu verwenden. Die folgenden Sätze hätten zum Beispiel jeweils einen Beweis, der mit unserem Beweis des Satzes (¬(P v Q)↔(¬P ^ ¬Q)) identisch ist, nur dass die Buchstaben unterschiedlich sind:

(¬(R v S) ↔ (¬R ^ ¬S))

(¬(T v U) ↔ (¬T ^ ¬U))

(¬(V v W) ↔ (¬V ^ ¬W))

Dies ist hoffentlich offensichtlich. Nehmen Sie den Beweis von (¬(P v Q)↔(¬P ^ ¬Q)), und ersetzen Sie in diesem Beweis jede Instanz von P durch R und jede Instanz von Q durch S, und Sie hätten einen Beweis von (¬(R v S)↔(¬R ^ ¬S)).

Aber hier ist etwas, das vielleicht weniger offensichtlich ist. Jede der folgenden Aussagen kann als ähnlich dem Theorem (¬(P v Q)↔(¬P ^ ¬Q)) betrachtet werden.

(¬((P^Q) v (R^S))↔(¬(P^Q) ^ ¬(R^S)))

(¬(T v (Q v V))↔(¬T ^ ¬(Q v V))

(¬((Q↔P) v (¬R→¬Q))↔(¬(Q↔P) ^ ¬(¬R→¬Q)))

Beispielsweise, Wenn man einen Beweis von (¬(P v Q)↔(¬P ^ ¬Q)) nimmt und jede Anfangsinstanz von P durch (Q↔P) und jede Anfangsinstanz von Q durch (¬R→¬Q) ersetzt, dann hätte man einen Beweis des Theorems (¬((Q↔P) v (¬R→¬Q))↔(¬(Q↔P) ^ ¬(¬R→¬Q))).

Wir können diese Erkenntnis auf zwei Arten erfassen. Wir könnten Theoreme unserer Metasprache angeben und zulassen, dass diese Instanzen haben. So könnten wir (¬(Φ v Ψ) ↔ (¬Φ ^ ¬Ψ)) als ein Theorem der Metasprache nehmen, in dem wir jedes Φ durch einen Satz und jedes Ψ durch einen Satz ersetzen können und so eine bestimmte Instanz eines Theorems erhalten. Eine Alternative besteht darin, zuzulassen, dass wir aus einem Satz durch Substitution andere Sätze erzeugen können. Der Einfachheit halber werden wir diese zweite Strategie wählen.

Unsere Regel wird wie folgt lauten. Sobald wir ein Theorem bewiesen haben, können wir es jederzeit in einem Beweis zitieren. Unsere Rechtfertigung ist, dass die Behauptung ein Theorem ist. Wir erlauben die Ersetzung eines beliebigen atomaren Satzes im Theorem durch einen anderen Satz nur dann, wenn wir jede anfängliche Instanz dieses atomaren Satzes im Theorem durch denselben Satz ersetzen.

Bevor wir ein Beispiel betrachten, ist es nützlich, einige nützliche Theoreme aufzuführen. Es gibt unendlich viele Theoreme in unserer Sprache, aber diese zehn sind oft sehr hilfreich. Ein paar haben wir bewiesen. Die anderen können als Übung bewiesen werden.

T1 (P v ¬P)

T2 (¬(P→Q) ↔ (P^¬Q))

T3 (¬(P v Q) ↔ (¬P ^ ¬Q))

T4 ((¬P v ¬Q) ↔ ¬(P ^ Q))

T5 (¬(P ↔ Q) ↔ (P ↔ ¬Q))

T6 (¬P → (P → Q))

T7 (P → (Q → P))

T8 ((P→(Q→R)) → ((P→Q) → (P→R)))

T9 ((¬P→¬Q) → ((¬P→Q) →P))

T10 ((P→Q) → (¬Q→¬P))

Ein paar Beispiele werden den Vorteil der Verwendung von Theoremen deutlich machen. Betrachten wir ein anderes Argument, das auf dem obigen aufbaut. Wir wissen, dass es weder der Fall ist, dass Smith, wenn er nach London geht, nach Berlin geht, noch dass es der Fall ist, dass Jones, wenn er nach London geht, nach Berlin geht. Wir wollen nun beweisen, dass es nicht der Fall ist, dass Jones nach Berlin geht. Wir fügen folgendes zu unserem Schlüssel hinzu:

R: Smith wird nach Berlin gehen.

S: Jones wird nach Berlin gehen.

Und wir haben das folgende Argument:

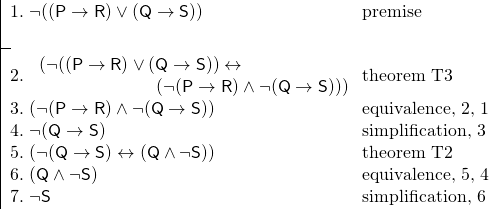
Durch die Verwendung von Theoremen ist dieser Beweis viel kürzer als er sonst sein könnte. Außerdem machen Theoreme einen Beweis oft leichter nachvollziehbar, da wir die Theoreme als Tautologien erkennen – als Sätze, die wahr sein müssen.

9.8 Probleme

1. Beweise, dass jedes der folgenden Argumente gültig ist.

1. Voraussetzungen: P, ¬Q. Schlussfolgerung: ¬(P↔Q).
2. Prämissen: (¬PvQ), (Pv¬Q). Schlussfolgerung: (P↔Q).
3. Prämissen: (P↔Q), (R↔S) . Folgerung: ((P^R)↔(Q^S)).

1. Beweisen Sie jeden der folgenden Lehrsätze.

1. T1
2. T2
3. T5
4. T6
5. T7
6. T8
7. T9
8. ((P^Q)↔¬(¬Pv¬Q))
9. ((P→Q)↔¬(P^¬Q))

1. Schreiben Sie in normalem umgangssprachlichen Englisch ein eigenes gültiges Argument mit mindestens zwei Prämissen, von denen mindestens eine eine bikonditionale ist. Dein Argument sollte nur ein Absatz sein (keine geordnete Liste von Sätzen oder etwas anderes, das wie formale Logik aussieht). Übersetzen Sie es in die Aussagenlogik und beweisen Sie, dass es gültig ist.
2. Schreiben Sie in normalem umgangssprachlichen Englisch ein eigenes gültiges Argument mit mindestens zwei Prämissen und einer Schlussfolgerung, die eine zweiwertige Bedingung ist. Dein Argument sollte nur ein Absatz sein (keine geordnete Liste von Sätzen oder etwas anderes, das formal wie Logik aussieht). Übersetze es in Aussagenlogik und beweise, dass es gültig ist.